plotPartialDependence
Create partial dependence plot (PDP) and individual conditional expectation (ICE) plots
Syntax
Description
plotPartialDependence(
computes and plots the partial dependence between the predictor variables listed
in RegressionMdl,Vars)Vars and model predictions. In this syntax, the model
predictions are the responses predicted by using the regression model
RegressionMdl, which contains predictor data.
If you specify one variable in
Vars, the function creates a line plot of the partial dependence against the variable.If you specify two variables in
Vars, the function creates a surface plot of the partial dependence against the two variables.
plotPartialDependence(
computes and plots the partial dependence between the predictor variables listed
in ClassificationMdl,Vars,Labels)Vars and the scores for the classes specified in
Labels by using the classification model
ClassificationMdl, which contains predictor data.
If you specify one variable in
Vars, the function creates a line plot of the partial dependence against the variable for each class inLabels.If you specify two variables in
Vars, the function creates a surface plot of the partial dependence against the two variables. You must specify one class inLabels.
plotPartialDependence(
computes and plots the partial dependence between the predictor variables listed
in fun,Vars,Data)Vars and the outputs returned by the custom model
fun, using the predictor data Data.
If you specify one variable in
Vars, the function creates a line plot of the partial dependence against the variable for each column of the output returned byfun.If you specify two variables in
Vars, the function creates a surface plot of the partial dependence against the two variables. When you specify two variables,funmust return a column vector or you must specify which output column to use by setting theOutputColumnsname-value argument.
plotPartialDependence(___,
uses additional options specified by one or more name-value arguments. For
example, if you specify Name,Value)"Conditional","absolute", the
plotPartialDependence function creates a figure
including a PDP, a scatter plot of the selected predictor variable and predicted
responses or scores, and an ICE plot for each observation.
Examples
Train a regression tree using the carsmall data set, and create a PDP that shows the relationship between a feature and the predicted responses in the trained regression tree.
Load the carsmall data set.
load carsmallSpecify Weight, Cylinders, and Horsepower as the predictor variables (X), and MPG as the response variable (Y).
X = [Weight,Cylinders,Horsepower]; Y = MPG;
Train a regression tree using X and Y.
Mdl = fitrtree(X,Y);
View a graphical display of the trained regression tree.
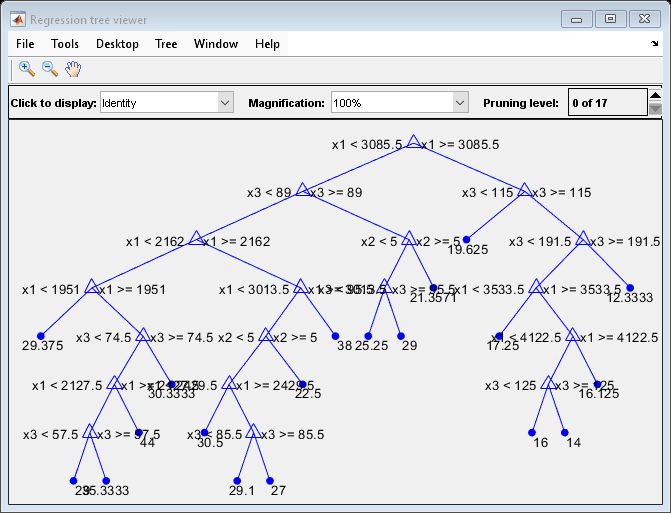
view(Mdl,"Mode","graph")
Create a PDP of the first predictor variable, Weight.
plotPartialDependence(Mdl,1)
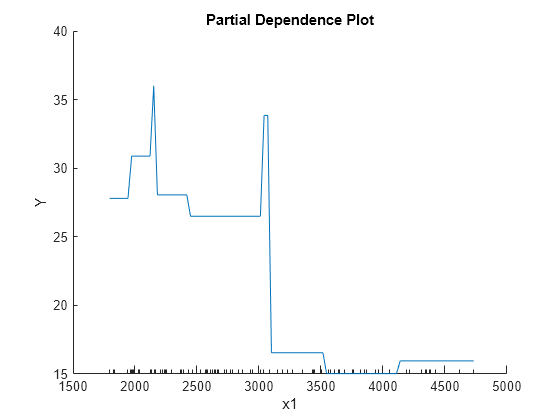
The plotted line represents averaged partial relationships between Weight (labeled as x1) and MPG (labeled as Y) in the trained regression tree Mdl. The x-axis minor ticks represent the unique values in x1.
The regression tree viewer shows that the first decision is whether x1 is smaller than 3085.5. The PDP also shows a large change near x1 = 3085.5. The tree viewer visualizes each decision at each node based on predictor variables. You can find several nodes split based on the values of x1, but determining the dependence of Y on x1 is not easy. However, the plotPartialDependence plots average predicted responses against x1, so you can clearly see the partial dependence of Y on x1.
The labels x1 and Y are the default values of the predictor names and the response name. You can modify these names by specifying the name-value arguments PredictorNames and ResponseName when you train Mdl using fitrtree. You can also modify axis labels by using the xlabel and ylabel functions.
Train a naive Bayes classification model with the fisheriris data set, and create a PDP that shows the relationship between the predictor variable and the predicted scores (posterior probabilities) for multiple classes.
Load the fisheriris data set, which contains species (species) and measurements (meas) on sepal length, sepal width, petal length, and petal width for 150 iris specimens. The data set contains 50 specimens from each of three species: setosa, versicolor, and virginica.
load fisheririsTrain a naive Bayes classification model with species as the response and meas as predictors.
Mdl = fitcnb(meas,species);
Create a PDP of the scores predicted by Mdl for all three classes of species against the third predictor variable x3. Specify the class labels by using the ClassNames property of Mdl.
plotPartialDependence(Mdl,3,Mdl.ClassNames);
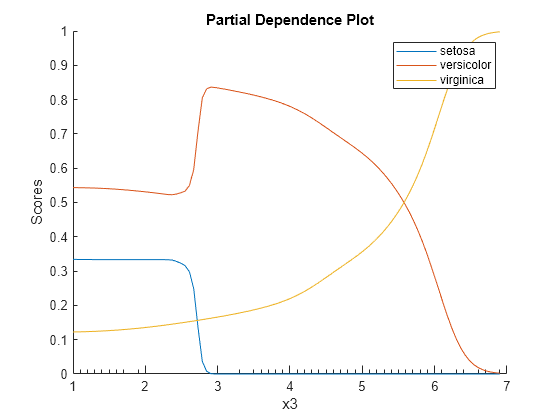
According to this model, the probability of virginica increases with x3. The probability of setosa is about 0.33, from where x3 is 0 to around 2.5, and then the probability drops to almost 0.
Train a Gaussian process regression model using generated sample data where a response variable includes interactions between predictor variables. Then, create ICE plots that show the relationship between a feature and the predicted responses for each observation.
Generate sample predictor data x1 and x2.
rng("default") % For reproducibility n = 200; x1 = rand(n,1)*2-1; x2 = rand(n,1)*2-1;
Generate response values that include interactions between x1 and x2.
Y = x1-2*x1.*(x2>0)+0.1*rand(n,1);
Create a Gaussian process regression model using [x1 x2] and Y.
Mdl = fitrgp([x1 x2],Y);
Create a figure including a PDP (red line) for the first predictor x1, a scatter plot (circle markers) of x1 and predicted responses, and a set of ICE plots (gray lines) by specifying Conditional as "centered".
plotPartialDependence(Mdl,1,"Conditional","centered")
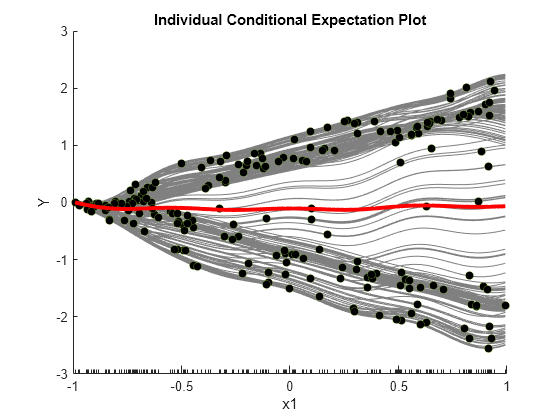
When Conditional is "centered", plotPartialDependence offsets plots so that all plots start from zero, which is helpful in examining the cumulative effect of the selected feature.
A PDP finds averaged relationships, so it does not reveal hidden dependencies especially when responses include interactions between features. However, the ICE plots clearly show two different dependencies of responses on x1.
Train an ensemble of classification models and create two PDPs, one using the training data set and the other using a new data set.
Load the census1994 data set, which contains US yearly salary data, categorized as <=50K or >50K, and several demographic variables.
load census1994Extract a subset of variables to analyze from the tables adultdata and adulttest.
X = adultdata(:,["age","workClass","education_num","marital_status","race", ... "sex","capital_gain","capital_loss","hours_per_week","salary"]); Xnew = adulttest(:,["age","workClass","education_num","marital_status","race", ... "sex","capital_gain","capital_loss","hours_per_week","salary"]);
Train an ensemble of classifiers with salary as the response and the remaining variables as predictors by using the function fitcensemble. For binary classification, fitcensemble aggregates 100 classification trees using the LogitBoost method.
Mdl = fitcensemble(X,"salary");Inspect the class names in Mdl.
Mdl.ClassNames
ans = 2×1 categorical
<=50K
>50K
Create a partial dependence plot of the scores predicted by Mdl for the second class of salary (>50K) against the predictor age using the training data.
plotPartialDependence(Mdl,"age",Mdl.ClassNames(2))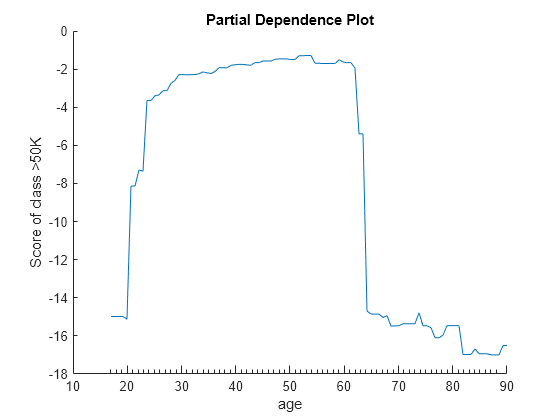
Create a PDP of the scores for class >50K against age using new predictor data from the table Xnew.
plotPartialDependence(Mdl,"age",Mdl.ClassNames(2),Xnew)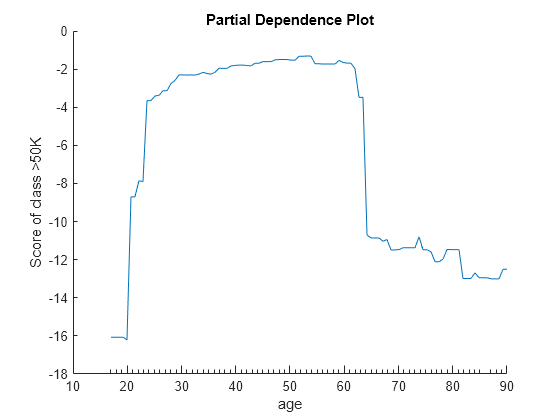
The two plots show similar shapes for the partial dependence of the predicted score of high salary (>50K) on age. Both plots indicate that the predicted score of high salary rises fast until the age of 30, then stays almost flat until the age of 60, and then drops fast. However, the plot based on the new data produces slightly higher scores for ages over 65.
Create a PDP to analyze relationships between predictors and anomaly scores for an isolationForest object. You cannot pass an isolationForest object directly to the plotPartialDependence function. Instead, define a custom function that returns anomaly scores for the object, and then pass the function to plotPartialDependence.
Load the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau.
load census1994census1994 contains the two data sets adultdata and adulttest.
Train an isolation forest model for adulttest. The function iforest returns an IsolationForest object.
rng("default") % For reproducibility Mdl = iforest(adulttest);
Define the custom function myAnomalyScores, which returns anomaly scores computed by the isanomaly function of IsolationForest; the custom function definition appears at the end of this example.
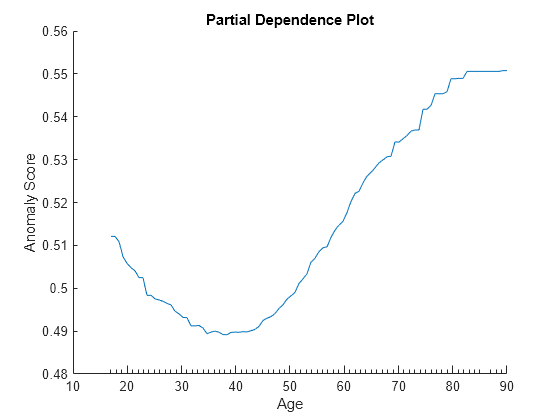
Create a PDP of the anomaly scores against the variable age for the adulttest data set. plotPartialDependence accepts a custom model in the form of a function handle. The function represented by the function handle must accept predictor data and return a column vector or matrix with one row for each observation. Specify the custom model as @(tbl)myAnomalyScores(Mdl,tbl) so that the custom function uses the trained model Mdl and accepts predictor data.
plotPartialDependence(@(tbl)myAnomalyScores(Mdl,tbl),"age",adulttest) xlabel("Age") ylabel("Anomaly Score")
Custom Function myAnomalyScores
function scores = myAnomalyScores(Mdl,tbl) [~,scores] = isanomaly(Mdl,tbl); end
Train a regression ensemble using the carsmall data set, and create a PDP plot and ICE plots for each predictor variable using a new data set, carbig. Then, compare the figures to analyze the importance of predictor variables. Also, compare the results with the estimates of predictor importance returned by the predictorImportance function.
Load the carsmall data set.
load carsmallSpecify Weight, Cylinders, Horsepower, and Model_Year as the predictor variables (X), and MPG as the response variable (Y).
X = [Weight,Cylinders,Horsepower,Model_Year]; Y = MPG;
Train a regression ensemble using X and Y.
Mdl = fitrensemble(X,Y, ... "PredictorNames",["Weight","Cylinders","Horsepower","Model Year"], ... "ResponseName","MPG");
Determine the importance of the predictor variables by using the plotPartialDependence and predictorImportance functions. The plotPartialDependence function visualizes the relationships between a selected predictor and predicted responses. predictorImportance summarizes the importance of a predictor with a single value.
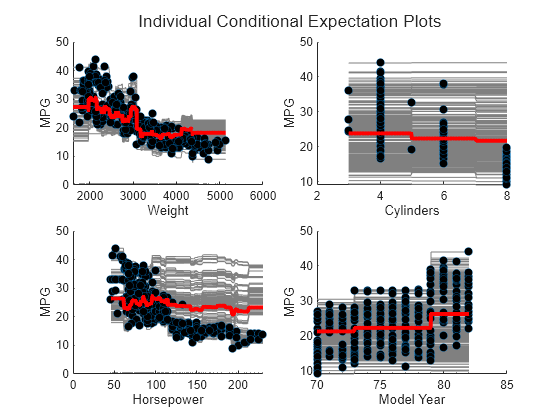
Create a figure including a PDP plot (red line) and ICE plots (gray lines) for each predictor by using plotPartialDependence and specifying "Conditional","absolute". Each figure also includes a scatter plot (circle markers) of the selected predictor and predicted responses. Also, load the carbig data set and use it as new predictor data, Xnew. When you provide Xnew, the plotPartialDependence function uses Xnew instead of the predictor data in Mdl.
load carbig Xnew = [Weight,Cylinders,Horsepower,Model_Year]; figure t = tiledlayout(2,2,"TileSpacing","compact"); title(t,"Individual Conditional Expectation Plots") for i = 1 : 4 nexttile plotPartialDependence(Mdl,i,Xnew,"Conditional","absolute") title("") end
Compute estimates of predictor importance by using predictorImportance. This function sums changes in the mean squared error (MSE) due to splits on every predictor, and then divides the sum by the number of branch nodes.
imp = predictorImportance(Mdl); figure bar(imp) title("Predictor Importance Estimates") ylabel("Estimates") xlabel("Predictors") ax = gca; ax.XTickLabel = Mdl.PredictorNames;
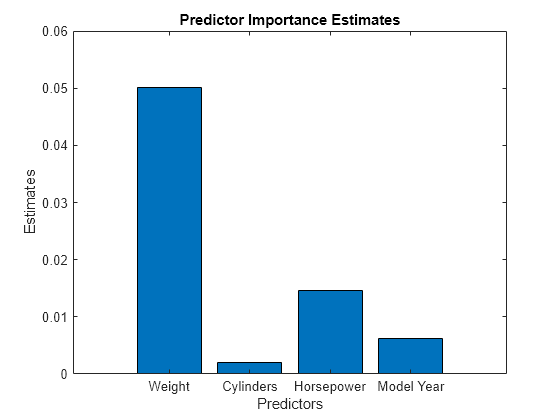
The variable Weight has the most impact on MPG according to predictor importance. The PDP of Weight also shows that MPG has high partial dependence on Weight. The variable Cylinders has the least impact on MPG according to predictor importance. The PDP of Cylinders also shows that MPG does not change much depending on Cylinders.
Train a generalized additive model (GAM) with both linear and interaction terms for predictors. Then, create a PDP with both linear and interaction terms and a PDP with only linear terms. Specify whether to include interaction terms when creating the PDPs.
Load the ionosphere data set. This data set has 34 predictors and 351 binary responses for radar returns, either bad ('b') or good ('g').
load ionosphereTrain a GAM using the predictors X and class labels Y. A recommended practice is to specify the class names. Specify to include the 10 most important interaction terms.
Mdl = fitcgam(X,Y,"ClassNames",{'b','g'},"Interactions",10);
Mdl is a ClassificationGAM model object.
List the interaction terms in Mdl.
Mdl.Interactions
ans = 10×2
1 5
7 8
6 7
5 6
5 7
5 8
3 5
4 7
1 7
4 5
Each row of Interactions represents one interaction term and contains the column indexes of the predictor variables for the interaction term.
Find the most frequent predictor in the interaction terms.
mode(Mdl.Interactions,"all")ans = 5
The most frequent predictor in the interaction terms is the 5th predictor (x5). Create PDPs for the 5th predictor. To exclude interaction terms from the computation, specify "IncludeInteractions",false for the second PDP.
plotPartialDependence(Mdl,5,Mdl.ClassNames(1)) hold on plotPartialDependence(Mdl,5,Mdl.ClassNames(1),"IncludeInteractions",false) grid on legend("Linear and interaction terms","Linear terms only") title("PDPs of Posterior Probabilities for 5th Predictor") hold off
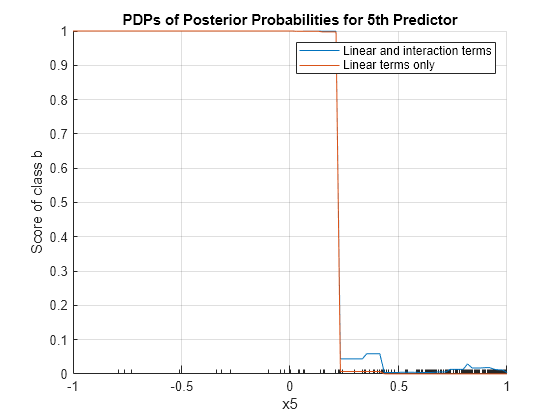
The plot shows that the partial dependence of the scores (posterior probabilities) on x5 varies depending on whether the model includes the interaction terms, especially where x5 is between 0.2 and 0.45.
Train a support vector machine (SVM) regression model using the carsmall data set, and create a PDP for two predictor variables. Then, extract partial dependence estimates from the output of plotPartialDependence. Alternatively, you can get the partial dependence values by using the partialDependence function.
Load the carsmall data set.
load carsmallSpecify Weight, Cylinders, Displacement, and Horsepower as the predictor variables (Tbl).
Tbl = table(Weight,Cylinders,Displacement,Horsepower);
Construct an SVM regression model using Tbl and the response variable MPG. Use a Gaussian kernel function with an automatic kernel scale.
Mdl = fitrsvm(Tbl,MPG,"ResponseName","MPG", ... "CategoricalPredictors","Cylinders","Standardize",true, ... "KernelFunction","gaussian","KernelScale","auto");
Create a PDP that visualizes partial dependence of predicted responses (MPG) on the predictor variables Weight and Cylinders. Specify query points to compute the partial dependence for Weight by using the QueryPoints name-value argument. You cannot specify the QueryPoints value for Cylinders because it is a categorical variable. plotPartialDependence uses all categorical values.
pt = linspace(min(Weight),max(Weight),50)'; ax = plotPartialDependence(Mdl,["Weight","Cylinders"],"QueryPoints",{pt,[]}); view(140,30) % Modify the viewing angle
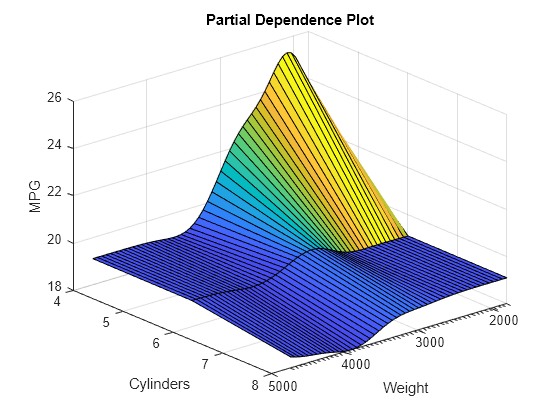
The PDP shows an interaction effect between Weight and Cylinders. The partial dependence of MPG on Weight changes depending on the value of Cylinders.
Extract the estimated partial dependence of MPG on Weight and Cylinders. The XData, YData, and ZData values of ax.Children are x-axis values (the first selected predictor values), y-axis values (the second selected predictor values), and z-axis values (the corresponding partial dependence values), respectively.
xval = ax.Children.XData; yval = ax.Children.YData; zval = ax.Children.ZData;
Alternatively, you can get the partial dependence values by using the partialDependence function.
[pd,x,y] = partialDependence(Mdl,["Weight","Cylinders"],"QueryPoints",{pt,[]});
pd contains the partial dependence values for the query points x and y.
If you specify Conditional as "absolute", plotPartialDependence creates a figure including a PDP, a scatter plot, and a set of ICE plots. ax.Children(1) and ax.Children(2) correspond to the PDP and scatter plot, respectively. The remaining elements of ax.Children correspond to the ICE plots. The XData and YData values of ax.Children(i) are x-axis values (the selected predictor values) and y-axis values (the corresponding partial dependence values), respectively.
Input Arguments
Regression model, specified as a full or compact regression model object, as given in the following tables of supported models.
| Model | Full or Compact Model Object |
|---|---|
| Generalized linear model | GeneralizedLinearModel, CompactGeneralizedLinearModel |
| Generalized linear mixed-effect model | GeneralizedLinearMixedModel |
| Linear regression | LinearModel, CompactLinearModel |
| Linear mixed-effect model | LinearMixedModel |
| Nonlinear regression | NonLinearModel |
| Censored linear regression | CensoredLinearModel, CompactCensoredLinearModel |
| Ensemble of regression models | RegressionEnsemble, RegressionBaggedEnsemble,
CompactRegressionEnsemble |
| Generalized additive model (GAM) | RegressionGAM, CompactRegressionGAM |
| Gaussian process regression | RegressionGP, CompactRegressionGP |
| Gaussian kernel regression model using random feature expansion | RegressionKernel |
| Linear regression for high-dimensional data | RegressionLinear |
| Neural network regression model | RegressionNeuralNetwork, CompactRegressionNeuralNetwork |
| Support vector machine (SVM) regression | RegressionSVM, CompactRegressionSVM |
| Regression tree | RegressionTree, CompactRegressionTree |
| Bootstrap aggregation for ensemble of decision trees | TreeBagger, CompactTreeBagger |
If
RegressionMdlis a model object that does not contain predictor data (for example, a compact model), you must provide the input argumentData.plotPartialDependencedoes not support a model object trained with a sparse matrix. When you train a model, use a full numeric matrix or table for predictor data where rows correspond to individual observations.plotPartialDependencedoes not support a model object trained with more than one response variable.
Classification model, specified as a full or compact classification model object, as given in the following table of supported models.
| Model | Full or Compact Model Object |
|---|---|
| Discriminant analysis classifier | ClassificationDiscriminant, CompactClassificationDiscriminant |
| Multiclass model for support vector machines or other classifiers | ClassificationECOC, CompactClassificationECOC |
| Ensemble of learners for classification | ClassificationEnsemble, CompactClassificationEnsemble, ClassificationBaggedEnsemble |
| Generalized additive model (GAM) | ClassificationGAM, CompactClassificationGAM |
| Gaussian kernel classification model using random feature expansion | ClassificationKernel |
| k-nearest neighbor classifier | ClassificationKNN |
| Linear classification model | ClassificationLinear |
| Multiclass naive Bayes model | ClassificationNaiveBayes, CompactClassificationNaiveBayes |
| Neural network classifier | ClassificationNeuralNetwork, CompactClassificationNeuralNetwork |
| Support vector machine (SVM) classifier for one-class and binary classification | ClassificationSVM, CompactClassificationSVM |
| Binary decision tree for multiclass classification | ClassificationTree, CompactClassificationTree |
| Bagged ensemble of decision trees | TreeBagger, CompactTreeBagger |
| Multinomial regression model | MultinomialRegression |
If ClassificationMdl is a model object that does not contain predictor
data (for example, a compact model), you must provide the input argument
Data.
plotPartialDependence does not support a model object trained with a sparse matrix. When you train a model, use a full numeric matrix or table for predictor data where rows correspond to individual observations.
Custom model, specified as a function handle. The function handle fun
must represent a function that accepts the predictor data Data and
returns an output in the form of a column vector or matrix. Each row of the output must
correspond to each observation (row) in the predictor data.
By default, plotPartialDependence uses all output columns of
fun for the partial dependence computation. You can specify
which output columns to use by setting the OutputColumns name-value
argument.
If the predictor data (Data) is in a table,
plotPartialDependence assumes that a variable is categorical if it is a
logical vector, categorical vector, character array, string array, or cell array of
character vectors. If the predictor data is a matrix, plotPartialDependence
assumes that all predictors are continuous. To identify any other predictors as
categorical predictors, specify them by using the
CategoricalPredictors name-value argument.
Data Types: function_handle
Predictor variables, specified as a vector of positive integers, character vector, string scalar, string array, or cell array of character vectors. You can specify one or two predictor variables, as shown in the following tables.
One Predictor Variable
| Value | Description |
|---|---|
| positive integer | Index value corresponding to the column of the predictor data. |
| character vector or string scalar | Name of the predictor variable. The name must match the entry in the
|
Two Predictor Variables
| Value | Description |
|---|---|
| vector of two positive integers | Index values corresponding to the columns of the predictor data. |
| string array or cell array of character vectors | Names of the predictor variables. Each element in the array is the name of a predictor
variable. The names must match the entries in the
|
If you specify two predictor variables, you must specify one class in
Labels for ClassificationMdl
or specify one output column in OutputColumns for a
custom model fun.
Example: ["x1","x3"]
Data Types: single | double | char | string | cell
Class labels, specified as a categorical or character array, logical or
numeric vector, or cell array of character vectors. The values and data
types in Labels must match those of the class names in
the ClassNames property of
ClassificationMdl
(ClassificationMdl.ClassNames).
You can specify multiple class labels only when you specify one variable in
Varsand specifyConditionalas"none"(default).Use
partialDependenceif you want to compute the partial dependence for two variables and multiple class labels in one function call.
This argument is valid only when you specify a classification model object
ClassificationMdl.
Example: ["red","blue"]
Example: ClassificationMdl.ClassNames([1 3]) specifies
Labels as the first and third classes in
ClassificationMdl.
Data Types: single | double | logical | char | cell | categorical
Predictor data, specified as a numeric matrix or table. Each row of
Data corresponds to one observation, and each column
corresponds to one variable.
For both a regression model (RegressionMdl) and a classification
model (ClassificationMdl), Data must be
consistent with the predictor data that trained the model, stored in either the
X or Variables property.
If you trained the model using a numeric matrix, then
Datamust be a numeric matrix. The variables that make up the columns ofDatamust have the same number and order as the predictor variables that trained the model.If you trained the model using a table (for example,
Tbl), thenDatamust be a table. All predictor variables inDatamust have the same variable names and data types as the names and types inTbl. However, the column order ofDatadoes not need to correspond to the column order ofTbl.Datamust not be sparse.
If you specify a regression or classification model that does not contain predictor
data, you must provide Data. If the model is a full model object
that contains predictor data and you specify the Data argument,
then plotPartialDependence ignores the predictor data in the model and uses
Data only.
If you specify a custom model fun, you must provide
Data.
Data Types: single | double | table
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: plotPartialDependence(Mdl,Vars,Data,"NumObservationsToSample",100,"UseParallel",true)
creates a PDP by using 100 sampled observations in
Datafor-loop iterations in parallel.
Plot type, specified as "none",
"absolute", or "centered".
| Value | Description |
|---|---|
"none" |
|
"absolute" |
To use the
|
"centered" |
To use the
|
Example: "Conditional","absolute"
Flag to include interaction terms of the generalized additive model (GAM) in the partial
dependence computation, specified as true or
false. This argument is valid only for a GAM. That is, you can
specify this argument only when RegressionMdl is RegressionGAM
or CompactRegressionGAM, or ClassificationMdl is ClassificationGAM or CompactClassificationGAM.
The default IncludeInteractions value is true if the
model contains interaction terms. The value must be false if the
model does not contain interaction terms.
Example: "IncludeInteractions",false
Data Types: logical
Flag to include an intercept term of the generalized additive model (GAM) in the partial
dependence computation, specified as true or
false. This argument is valid only for a GAM. That is, you can
specify this argument only when RegressionMdl is RegressionGAM
or CompactRegressionGAM, or ClassificationMdl is ClassificationGAM or CompactClassificationGAM.
Example: "IncludeIntercept",false
Data Types: logical
Number of observations to sample, specified as a positive integer. The default value is the
number of total observations in Data or the model
(RegressionMdl or ClassificationMdl). If you
specify a value larger than the number of total observations, then
plotPartialDependence uses all observations.
plotPartialDependence samples observations without replacement by using the
datasample function and uses the sampled observations to compute partial
dependence.
plotPartialDependence displays minor tick marks
at the unique values of the sampled observations.
If you specify Conditional as either
"absolute" or "centered",
plotPartialDependence creates a figure including an ICE
plot for each sampled observation.
Example: "NumObservationsToSample",100
Data Types: single | double
Axes in which to plot, specified as an axes object. If you do not
specify the axes and if the current axes are Cartesian, then
plotPartialDependence uses the current axes
(gca). If axes do not exist,
plotPartialDependence plots in a new
figure.
Example: "Parent",ax
Points to compute partial dependence for numeric predictors, specified as a numeric column vector, a numeric two-column matrix, or a cell array of two numeric column vectors.
If you select one predictor variable in
Vars, use a numeric column vector.If you select two predictor variables in
Vars:Use a numeric two-column matrix to specify the same number of points for each predictor variable.
Use a cell array of two numeric column vectors to specify a different number of points for each predictor variable.
The default value is a numeric column vector or a numeric two-column matrix, depending on the number of selected predictor variables. Each column contains 100 evenly spaced points between the minimum and maximum values of the sampled observations for the corresponding predictor variable.
If Conditional is "absolute"
or "centered", then the software adds the predictor
data values (Data or predictor data in
RegressionMdl or
ClassificationMdl) of the selected predictors
to the query points.
You cannot modify QueryPoints for a categorical
variable. The plotPartialDependence function uses all
categorical values in the selected variable.
If you select one numeric variable and one categorical variable, you
can specify QueryPoints for a numeric variable by
using a cell array consisting of a numeric column vector and an empty
array.
Example: "QueryPoints",{pt,[]}
Data Types: single | double | cell
Flag to run in parallel, specified as true or
false. If you specify "UseParallel",true, the
plotPartialDependence function executes for-loop
iterations by using parfor when predicting responses or
scores for each observation and averaging them. The loop runs in parallel when you have
Parallel Computing Toolbox™.
Example: "UseParallel",true
Data Types: logical
Categorical predictors list for the custom model fun, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers | Each entry in the vector is an index value indicating that the corresponding predictor is categorical. The index values are between 1 and |
| Logical vector | A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the variable names of the predictor data Data in a table. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the variable names of the predictor data Data in a table. |
"all" | All predictors are categorical. |
By default, if the predictor data Data is in a table, plotPartialDependence assumes that a variable is categorical if it is a logical vector, categorical vector, character array, string array, or cell array of character vectors. If the predictor data is a matrix, plotPartialDependence assumes that all predictors are continuous. To identify any other predictors as categorical predictors, specify them by using the CategoricalPredictors name-value argument.
This argument is valid only when you specify a custom model by using fun.
Example: "CategoricalPredictors","all"
Data Types: single | double | logical | char | string | cell
Output columns of the custom model fun to use for the partial dependence computation, specified as one of the values in this table.
| Value | Description |
|---|---|
| Vector of positive integers | Each entry in the vector is an index value indicating that |
| Logical vector | A |
"all" | plotPartialDependence uses all output columns for the partial dependence computation. |
You can specify multiple output columns only when you specify one variable in
Varsand specifyConditionalas"none"(default).Use
partialDependenceif you want to compute the partial dependence for two variables and multiple output columns in one function call.
This argument is valid only when you specify a custom model by using
fun.
Example: "OutputColumns",[1 2]
Data Types: single | double | logical | char | string
Since R2024a
Predicted response value to use for observations with missing
predictor values, specified as "median",
"mean", or a numeric scalar.
| Value | Description |
|---|---|
"median" | plotPartialDependence uses the median of
the observed response values in the training data as the
predicted response value for observations with missing
predictor values. |
"mean" | plotPartialDependence uses the mean of the
observed response values in the training data as the
predicted response value for observations with missing
predictor values. |
| Numeric scalar |
If you specify
|
If an observation has a missing value in a Vars
predictor variable, then plotPartialDependence does not use
the observation in partial dependence computations and plots.
If the Conditional value is
"absolute" or "centered", then
the value of PredictionForMissingValue determines
the predicted response value for query points with new categorical
predictor values (that is, categories not used in training
RegressionMdl).
Note
This name-value argument is valid only for these types of
regression models: Gaussian process regression, kernel, linear,
neural network, and support vector machine. That is, you can specify
this argument only when RegressionMdl is a
RegressionGP,
CompactRegressionGP,
RegressionKernel,
RegressionLinear,
RegressionNeuralNetwork,
CompactRegressionNeuralNetwork,
RegressionSVM, or
CompactRegressionSVM object.
Example: "PredictionForMissingValue","mean"
Example: "PredictionForMissingValue",NaN
Data Types: single | double | char | string
Output Arguments
Axes of the plot, returned as an axes object. For details on how to modify the appearance of the axes and extract data from plots, see Axes Appearance and Extract Partial Dependence Estimates from Plots.
More About
Partial dependence [1] represents the relationships between
predictor variables and predicted responses in a trained regression model.
plotPartialDependence computes the partial dependence of predicted responses
on a subset of predictor variables by marginalizing over the other variables.
Consider partial dependence on a subset XS of the whole predictor variable set X = {x1, x2, …, xm}. A subset XS includes either one variable or two variables: XS = {xS1} or XS = {xS1, xS2}. Let XC be the complementary set of XS in X. A predicted response f(X) depends on all variables in X:
f(X) = f(XS, XC).
The partial dependence of predicted responses on XS is defined by the expectation of predicted responses with respect to XC:
where
pC(XC)
is the marginal probability of XC, that is, . Assuming that each observation is equally likely, and the dependence
between XS and
XC and the interactions of
XS and
XC in responses is not strong,
plotPartialDependence estimates the partial dependence by using observed
predictor data as follows:
| (1) |
where N is the number of observations and Xi = (XiS, XiC) is the ith observation.
When you call the plotPartialDependence function, you can specify a trained
model (f(·)) and select variables
(XS) by using the input arguments
RegressionMdl and Vars, respectively.
plotPartialDependence computes the partial dependence at 100 evenly spaced
points of XS or the points that you specify by
using the QueryPoints name-value argument. You can specify the number
(N) of observations to sample from given predictor data by using the
NumObservationsToSample name-value argument.
An individual conditional expectation (ICE) [2], as an extension of partial dependence, represents the relationship between a predictor variable and the predicted responses for each observation. While partial dependence shows the averaged relationship between predictor variables and predicted responses, a set of ICE plots disaggregates the averaged information and shows an individual dependence for each observation.
plotPartialDependence creates an ICE plot
for each observation. A set of ICE plots is useful to investigate heterogeneities of
partial dependence originating from different observations.
plotPartialDependence can also create ICE plots with any
predictor data provided through the input argument Data. You
can use this feature to explore predicted response space.
Consider an ICE plot for a selected predictor variable xS with a given observation XiC, where XS = {xS}, XC is the complementary set of XS in the whole variable set X, and Xi = (XiS, XiC) is the ith observation. The ICE plot corresponds to the summand of the summation in Equation 1:
plotPartialDependence plots for each observation i when you specify
Conditional as "absolute". If you
specify Conditional as "centered",
plotPartialDependence draws all plots after removing level
effects due to different observations:
This subtraction ensures that each plot starts from zero, so that you can examine the cumulative effect of XS and the interactions between XS and XC.
In the case of classification models,
plotPartialDependence computes the partial dependence and
individual conditional expectation in the same way as for regression models, with
one exception: instead of using the predicted responses from the model, the function
uses the predicted scores for the classes specified in
Labels.
The weighted traversal algorithm [1] is a method to estimate partial dependence for a tree-based model. The estimated partial dependence is the weighted average of response or score values corresponding to the leaf nodes visited during the tree traversal.
Let XS be a subset of the whole variable set X and XC be the complementary set of XS in X. For each XS value to compute partial dependence, the algorithm traverses a tree from the root (beginning) node down to leaf (terminal) nodes and finds the weights of leaf nodes. The traversal starts by assigning a weight value of one at the root node. If a node splits by XS, the algorithm traverses to the appropriate child node depending on the XS value. The weight of the child node becomes the same value as its parent node. If a node splits by XC, the algorithm traverses to both child nodes. The weight of each child node becomes a value of its parent node multiplied by the fraction of observations corresponding to each child node. After completing the tree traversal, the algorithm computes the weighted average by using the assigned weights.
For an ensemble of bagged trees, the estimated partial dependence is an average of the weighted averages over the individual trees.
Algorithms
For both a regression model (RegressionMdl) and a classification
model (ClassificationMdl),
plotPartialDependence uses a predict
function to predict responses or scores. plotPartialDependence
chooses the proper predict function according to the model and runs
predict with its default settings. For details about each
predict function, see the predict functions in
the following two tables. If the specified model is a tree-based model (not including a
boosted ensemble of trees) and Conditional is
"none", then plotPartialDependence uses the
weighted traversal algorithm instead of the predict function. For
details, see Weighted Traversal Algorithm.
Regression Model Object
| Model Type | Full or Compact Regression Model Object | Function to Predict Responses |
|---|---|---|
| Bootstrap aggregation for ensemble of decision trees | CompactTreeBagger | predict |
| Bootstrap aggregation for ensemble of decision trees | TreeBagger | predict |
| Ensemble of regression models | RegressionEnsemble, RegressionBaggedEnsemble, CompactRegressionEnsemble | predict |
| Gaussian kernel regression model using random feature expansion | RegressionKernel | predict |
| Gaussian process regression | RegressionGP, CompactRegressionGP | predict |
| Generalized additive model | RegressionGAM, CompactRegressionGAM | predict |
| Generalized linear mixed-effect model | GeneralizedLinearMixedModel | predict |
| Generalized linear model | GeneralizedLinearModel, CompactGeneralizedLinearModel | predict |
| Linear mixed-effect model | LinearMixedModel | predict |
| Linear regression | LinearModel, CompactLinearModel | predict |
| Linear regression for high-dimensional data | RegressionLinear | predict |
| Neural network regression model | RegressionNeuralNetwork, CompactRegressionNeuralNetwork | predict |
| Nonlinear regression | NonLinearModel | predict |
| Censored linear regression | CensoredLinearModel, CompactCensoredLinearModel | predict |
| Regression tree | RegressionTree, CompactRegressionTree | predict |
| Support vector machine | RegressionSVM, CompactRegressionSVM | predict |
Classification Model Object
Alternative Functionality
partialDependencecomputes partial dependence without visualization. The function can compute partial dependence for two variables and multiple classes in one function call.
References
[1] Friedman, Jerome. H. “Greedy Function Approximation: A Gradient Boosting Machine.” The Annals of Statistics 29, no. 5 (2001): 1189-1232.
[2] Goldstein, Alex, Adam Kapelner, Justin Bleich, and Emil Pitkin. “Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation.” Journal of Computational and Graphical Statistics 24, no. 1 (January 2, 2015): 44–65.
[3] Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. The Elements of Statistical Learning. New York, NY: Springer New York, 2001.
Extended Capabilities
To run in parallel, set the UseParallel name-value argument to
true in the call to this function.
For more general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Usage notes and limitations:
This function fully supports GPU arrays for the following regression and classification models:
LinearModelandCompactLinearModelobjectsGeneralizedLinearModelandCompactGeneralizedLinearModelobjectsRegressionKernelandClassificationKernelobjectsRegressionSVMandCompactRegressionSVMobjectsRegressionNeuralNetworkandCompactRegressionNeuralNetworkobjectsClassificationNeuralNetworkandCompactClassificationNeuralNetworkRegressionLinearobjectsClassificationLinearobjects
This function supports GPU arrays with limitations for the regression and classification models described in this table.
Full or Compact Model Object Limitations ClassificationECOCorCompactClassificationECOCBinary learners are subject to limitations depending on type:
Ensemble learners have the same limitations as
ClassificationEnsemble.KNN learners have the same limitations as
ClassificationKNNSVM learners have the same limitations as
ClassificationSVMTree learners have the same limitations as
ClassificationTree
ClassificationEnsemble,CompactClassificationEnsemble,RegressionEnsemble, orCompactRegressionEnsembleWeak learners are subject to limitations depending on type:
KNN learners have the same limitations as
ClassificationKNN.Tree learners have the same limitations as
ClassificationTree.Discriminant learners are not supported.
ClassificationKNNModels trained using the Kd-tree nearest neighbor search method, function handle or
fastdistance metrics, or tie inclusion are not supported.ClassificationSVMorCompactClassificationSVMOne-class classification is not supported
ClassificationTree,CompactClassificationTree,RegressionTree, orCompactRegressionTreeSurrogate splits are not supported for decision trees.
This function fully supports GPU arrays for a custom function if the custom function supports GPU arrays.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2017bplotPartialDependence allows you to specify censored linear regression models
using a CensoredLinearModel or CompactCensoredLinearModel
object.
plotPartialDependence fully supports GPU arrays for RegressionKernel and ClassificationKernel models.
plotPartialDependence fully supports GPU arrays for RegressionNeuralNetwork, CompactRegressionNeuralNetwork, ClassificationNeuralNetwork, and CompactClassificationNeuralNetwork models.
If RegressionMdl is a Gaussian process regression, kernel,
linear, neural network, or support vector machine model, you can now use
observations with missing predictor values in partial dependence computations and
plots. Specify the PredictionForMissingValue name-value
argument.
A value of
"median"is consistent with the behavior in R2023b.A value of
NaNis consistent with the behavior in R2023a, where the regression models do not support using observations with missing predictor values for prediction.
plotPartialDependence fully supports GPU arrays for
RegressionLinear models.
Starting in R2024a, plotPartialDependence fully supports GPU arrays for
ClassificationLinear models.
Starting in R2023a, plotPartialDependence fully supports GPU arrays for
RegressionSVM and
CompactRegressionSVM models.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)