predict
Class: ClassificationLinear
Predict labels for linear classification models
Syntax
Description
[
also returns classification scores for both
classes using any of the input argument combinations in the previous syntaxes.
Label,Score]
= predict(___)Score contains classification scores for each regularization strength
in Mdl.
Input Arguments
Binary, linear classification model, specified as a ClassificationLinear model object.
You can create a ClassificationLinear model object
using fitclinear.
Predictor data to be classified, specified as a full or sparse numeric matrix or a table.
By default, each row of X corresponds to one observation, and
each column corresponds to one variable.
For a numeric matrix:
The variables in the columns of
Xmust have the same order as the predictor variables that trainedMdl.If you train
Mdlusing a table (for example,Tbl) andTblcontains only numeric predictor variables, thenXcan be a numeric matrix. To treat numeric predictors inTblas categorical during training, identify categorical predictors by using theCategoricalPredictorsname-value pair argument offitclinear. IfTblcontains heterogeneous predictor variables (for example, numeric and categorical data types) andXis a numeric matrix, thenpredictthrows an error.
For a table:
predictdoes not support multicolumn variables or cell arrays other than cell arrays of character vectors.If you train
Mdlusing a table (for example,Tbl), then all predictor variables inXmust have the same variable names and data types as the variables that trainedMdl(stored inMdl.PredictorNames). However, the column order ofXdoes not need to correspond to the column order ofTbl. Also,TblandXcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.If you train
Mdlusing a numeric matrix, then the predictor names inMdl.PredictorNamesmust be the same as the corresponding predictor variable names inX. To specify predictor names during training, use thePredictorNamesname-value pair argument offitclinear. All predictor variables inXmust be numeric vectors.Xcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify 'ObservationsIn','columns', then you might experience a
significant reduction in optimization execution time. You cannot specify
'ObservationsIn','columns' for predictor data in a table.
Data Types: table | double | single
Predictor data observation dimension, specified as 'columns' or
'rows'.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify 'ObservationsIn','columns', then you might experience a
significant reduction in optimization execution time. You cannot specify
'ObservationsIn','columns' for predictor data in a table.
Output Arguments
Predicted class labels, returned as a categorical or character array, logical or numeric matrix, or cell array of character vectors.
The predict function classifies an observation into the class yielding the highest score. For an observation with NaN scores, the
function classifies the observation into the majority class, which makes up the largest
proportion of the training labels.
In most cases, Label is an n-by-L
array of the same data type as the observed class labels (Y) used to
train Mdl. (The software treats string arrays as cell arrays of character
vectors.)
n is the number of observations in X and
L is the number of regularization strengths in
Mdl.Lambda. That is,
Label(
is the predicted class label for observation i,j)i using the
linear classification model that has regularization strength
Mdl.Lambda(.j)
If Y is a character array and L >
1, then Label is a cell array of class labels.
Classification
scores, returned as a n-by-2-by-L numeric
array. n is the number of observations in X and L is
the number of regularization strengths in Mdl.Lambda. Score( is
the score for classifying observation i,k,j)i into
class k using the linear classification
model that has regularization strength Mdl.Lambda(. j)Mdl.ClassNames stores
the order of the classes.
If Mdl.Learner is 'logistic',
then classification scores are posterior probabilities.
Examples
Load the NLP data set.
load nlpdataX is a sparse matrix of predictor data, and Y is a categorical vector of class labels. There are more than two classes in the data.
The models should identify whether the word counts in a web page are from the Statistics and Machine Learning Toolbox™ documentation. So, identify the labels that correspond to the Statistics and Machine Learning Toolbox™ documentation web pages.
Ystats = Y == 'stats';Train a binary, linear classification model using the entire data set, which can identify whether the word counts in a documentation web page are from the Statistics and Machine Learning Toolbox™ documentation.
rng(1); % For reproducibility
Mdl = fitclinear(X,Ystats);Mdl is a ClassificationLinear model.
Predict the training-sample, or resubstitution, labels.
label = predict(Mdl,X);
Because there is one regularization strength in Mdl, label is column vectors with lengths equal to the number of observations.
Construct a confusion matrix.
ConfusionTrain = confusionchart(Ystats,label);
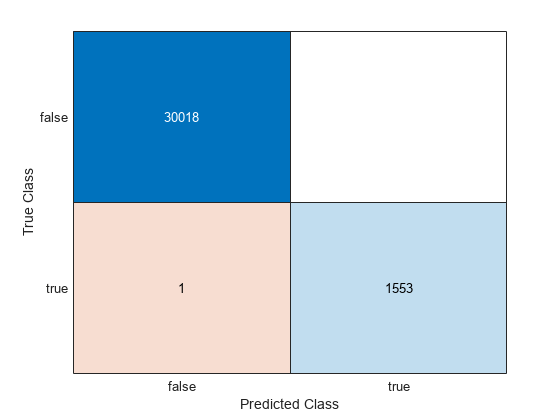
The model misclassifies only one 'stats' documentation page as being outside of the Statistics and Machine Learning Toolbox documentation.
Load the NLP data set and preprocess it as in Predict Training-Sample Labels. Transpose the predictor data matrix.
load nlpdata Ystats = Y == 'stats'; X = X';
Train a binary, linear classification model that can identify whether the word counts in a documentation web page are from the Statistics and Machine Learning Toolbox™ documentation. Specify to hold out 30% of the observations. Optimize the objective function using SpaRSA.
rng(1) % For reproducibility CVMdl = fitclinear(X,Ystats,'Solver','sparsa','Holdout',0.30,... 'ObservationsIn','columns'); Mdl = CVMdl.Trained{1};
CVMdl is a ClassificationPartitionedLinear model. It contains the property Trained, which is a 1-by-1 cell array holding a ClassificationLinear model that the software trained using the training set.
Extract the training and test data from the partition definition.
trainIdx = training(CVMdl.Partition); testIdx = test(CVMdl.Partition);
Predict the training- and test-sample labels.
labelTrain = predict(Mdl,X(:,trainIdx),'ObservationsIn','columns'); labelTest = predict(Mdl,X(:,testIdx),'ObservationsIn','columns');
Because there is one regularization strength in Mdl, labelTrain and labelTest are column vectors with lengths equal to the number of training and test observations, respectively.
Construct a confusion matrix for the training data.
ConfusionTrain = confusionchart(Ystats(trainIdx),labelTrain);
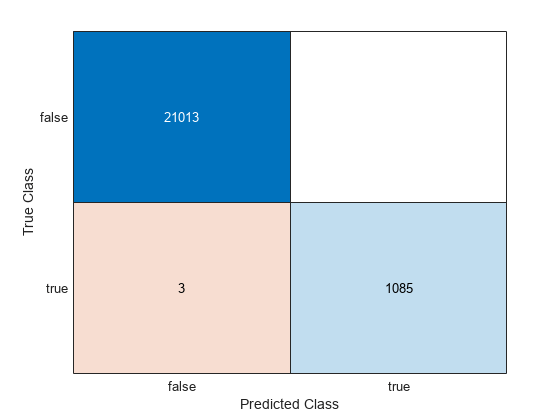
The model misclassifies only three documentation pages as being outside of Statistics and Machine Learning Toolbox documentation.
Construct a confusion matrix for the test data.
ConfusionTest = confusionchart(Ystats(testIdx),labelTest);
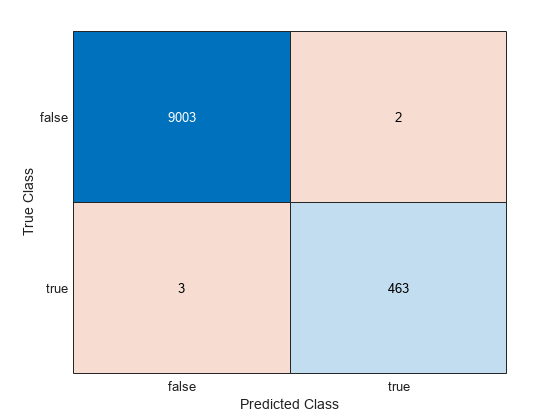
The model misclassifies three documentation pages as being outside the Statistics and Machine Learning Toolbox, and two pages as being inside.
Estimate test-sample, posterior class probabilities, and determine the quality of the model by plotting a receiver operating characteristic (ROC) curve. Linear classification models return posterior probabilities for logistic regression learners only.
Load the NLP data set and preprocess it as in Predict Test-Sample Labels.
load nlpdata Ystats = Y == 'stats'; X = X';
Randomly partition the data into training and test sets by specifying a 30% holdout sample. Identify the test-set indices.
cvp = cvpartition(Ystats,'Holdout',0.30);
idxTest = test(cvp);Train a binary linear classification model. Fit logistic regression learners using SpaRSA. To hold out the test set, specify the partitioned model.
CVMdl = fitclinear(X,Ystats,'ObservationsIn','columns','CVPartition',cvp,... 'Learner','logistic','Solver','sparsa'); Mdl = CVMdl.Trained{1};
Mdl is a ClassificationLinear model trained using the training set specified in the partition cvp only.
Predict the test-sample posterior class probabilities.
[~,posterior] = predict(Mdl,X(:,idxTest),'ObservationsIn','columns');
Because there is one regularization strength in Mdl, posterior is a matrix with 2 columns and rows equal to the number of test-set observations. Column i contains posterior probabilities of Mdl.ClassNames(i) given a particular observation.
Compute the performance metrics (true positive rates and false positive rates) for a ROC curve and find the area under the ROC curve (AUC) value by creating a rocmetrics object.
rocObj = rocmetrics(Ystats(idxTest),posterior,Mdl.ClassNames);
Plot the ROC curve for the second class by using the plot function of rocmetrics.
plot(rocObj,ClassNames=Mdl.ClassNames(2))

The ROC curve indicates that the model classifies the test-sample observations almost perfectly.
To determine a good lasso-penalty strength for a linear classification model that uses a logistic regression learner, compare test-sample values of the AUC.
Load the NLP data set. Preprocess the data as in Predict Test-Sample Labels.
load nlpdata Ystats = Y == 'stats'; X = X';
Create a data partition that specifies to holdout 10% of the observations. Extract test-sample indices.
rng(10); % For reproducibility Partition = cvpartition(Ystats,'Holdout',0.10); testIdx = test(Partition); XTest = X(:,testIdx); n = sum(testIdx)
n = 3157
YTest = Ystats(testIdx);
There are 3157 observations in the test sample.
Create a set of 11 logarithmically-spaced regularization strengths from through .
Lambda = logspace(-6,-0.5,11);
Train binary, linear classification models that use each of the regularization strengths. Optimize the objective function using SpaRSA. Lower the tolerance on the gradient of the objective function to 1e-8.
CVMdl = fitclinear(X,Ystats,'ObservationsIn','columns',... 'CVPartition',Partition,'Learner','logistic','Solver','sparsa',... 'Regularization','lasso','Lambda',Lambda,'GradientTolerance',1e-8)
CVMdl =
ClassificationPartitionedLinear
CrossValidatedModel: 'Linear'
ResponseName: 'Y'
NumObservations: 31572
KFold: 1
Partition: [1×1 cvpartition]
ClassNames: [0 1]
ScoreTransform: 'none'
Properties, Methods
Extract the trained linear classification model.
Mdl1 = CVMdl.Trained{1}Mdl1 =
ClassificationLinear
ResponseName: 'Y'
ClassNames: [0 1]
ScoreTransform: 'logit'
Beta: [34023×11 double]
Bias: [-11.9079 -11.9079 -11.9079 -11.9079 -9.3362 -6.4290 -5.1424 -4.4991 -3.5732 -3.1742 -2.9839]
Lambda: [1.0000e-06 3.5481e-06 1.2589e-05 4.4668e-05 1.5849e-04 5.6234e-04 0.0020 0.0071 0.0251 0.0891 0.3162]
Learner: 'logistic'
Properties, Methods
Mdl is a ClassificationLinear model object. Because Lambda is a sequence of regularization strengths, you can think of Mdl as 11 models, one for each regularization strength in Lambda.
Estimate the test-sample predicted labels and posterior class probabilities.
[label,posterior] = predict(Mdl1,XTest,'ObservationsIn','columns'); Mdl1.ClassNames; posterior(3,1,5)
ans = 1.0000
label is a 3157-by-11 matrix of predicted labels. Each column corresponds to the predicted labels of the model trained using the corresponding regularization strength. posterior is a 3157-by-2-by-11 matrix of posterior class probabilities. Columns correspond to classes and pages correspond to regularization strengths. For example, posterior(3,1,5) indicates that the posterior probability that the first class (label 0) is assigned to observation 3 by the model that uses Lambda(5) as a regularization strength is 1.0000.
For each model, compute the AUC by using rocmetrics.
auc = 1:numel(Lambda); % Preallocation for j = 1:numel(Lambda) rocObj = rocmetrics(YTest,posterior(:,:,j),Mdl1.ClassNames); auc(j) = rocObj.AUC(1); end
Higher values of Lambda lead to predictor variable sparsity, which is a good quality of a classifier. For each regularization strength, train a linear classification model using the entire data set and the same options as when you trained the model. Determine the number of nonzero coefficients per model.
Mdl = fitclinear(X,Ystats,'ObservationsIn','columns',... 'Learner','logistic','Solver','sparsa','Regularization','lasso',... 'Lambda',Lambda,'GradientTolerance',1e-8); numNZCoeff = sum(Mdl.Beta~=0);
In the same figure, plot the test-sample error rates and frequency of nonzero coefficients for each regularization strength. Plot all variables on the log scale.
figure yyaxis left plot(log10(Lambda),log10(auc),'o-') ylabel('log_{10} AUC') yyaxis right plot(log10(Lambda),log10(numNZCoeff + 1),'o-') ylabel('log_{10} nonzero-coefficient frequency') xlabel('log_{10} Lambda') title('Test-Sample Statistics') hold off

Choose the index of the regularization strength that balances predictor variable sparsity and high AUC. In this case, a value between to should suffice.
idxFinal = 9;
Select the model from Mdl with the chosen regularization strength.
MdlFinal = selectModels(Mdl,idxFinal);
MdlFinal is a ClassificationLinear model containing one regularization strength. To estimate labels for new observations, pass MdlFinal and the new data to predict.
More About
For linear classification models, the raw classification score for classifying the observation x, a row vector, into the positive class is defined by
For the model with regularization strength j, is the estimated column vector of coefficients (the model property
Beta(:,j)) and is the estimated, scalar bias (the model property
Bias(j)).
The raw classification score for classifying x into the negative class is –f(x). The software classifies observations into the class that yields the positive score.
If the linear classification model consists of logistic regression learners, then the
software applies the 'logit' score transformation to the raw
classification scores (see ScoreTransform).
Alternative Functionality
Simulink Block
To integrate the prediction of a linear classification model into Simulink®, you can use the ClassificationLinear
Predict block in the Statistics and Machine Learning Toolbox™ library or a MATLAB® Function block with the predict function. For examples,
see Predict Class Labels Using ClassificationLinear Predict Block and Predict Class Labels Using MATLAB Function Block.
When deciding which approach to use, consider the following:
If you use the Statistics and Machine Learning Toolbox library block, you can use the Fixed-Point Tool (Fixed-Point Designer) to convert a floating-point model to fixed point.
Support for variable-size arrays must be enabled for a MATLAB Function block with the
predictfunction.If you use a MATLAB Function block, you can use MATLAB functions for preprocessing or post-processing before or after predictions in the same MATLAB Function block.
Extended Capabilities
The
predict function supports tall arrays with the following usage
notes and limitations:
predictdoes not support talltabledata.
For more information, see Tall Arrays.
Usage notes and limitations:
You can generate C/C++ code for both
predictandupdateby using a coder configurer. Or, generate code only forpredictby usingsaveLearnerForCoder,loadLearnerForCoder, andcodegen.Code generation for
predictandupdate— Create a coder configurer by usinglearnerCoderConfigurerand then generate code by usinggenerateCode. Then you can update model parameters in the generated code without having to regenerate the code.Code generation for
predict— Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls thepredictfunction. Then usecodegen(MATLAB Coder) to generate code for the entry-point function.
To generate single-precision C/C++ code for
predict, specifyDataType="single"when you call theloadLearnerForCoderfunction.This table contains notes about the arguments of
predict. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlFor the usage notes and limitations of the model object, see Code Generation of the
ClassificationLinearobject.XFor general code generation,
Xmust be a single-precision or double-precision matrix or a table containing numeric variables, categorical variables, or both.In the coder configurer workflow,
Xmust be a single-precision or double-precision matrix.The number of observations in
Xcan be a variable size, but the number of variables inXmust be fixed.If you want to specify
Xas a table, then your model must be trained using a table, and your entry-point function for prediction must do the following:Accept data as arrays.
Create a table from the data input arguments and specify the variable names in the table.
Pass the table to
predict.
For an example of this table workflow, see Generate Code to Classify Data in Table. For more information on using tables in code generation, see Code Generation for Tables (MATLAB Coder) and Table Limitations for Code Generation (MATLAB Coder).
Name-value pair arguments Names in name-value arguments must be compile-time constants.
The value for the
'ObservationsIn'name-value pair argument must be a compile-time constant. For example, to use the'ObservationsIn','columns'name-value pair argument in the generated code, include{coder.Constant('ObservationsIn'),coder.Constant('columns')}in the-argsvalue ofcodegen(MATLAB Coder).
For more information, see Introduction to Code Generation.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2016apredict fully supports GPU arrays.
See Also
ClassificationLinear | loss | fitclinear | confusionchart | rocmetrics | testcholdout
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)