predict
Classify observations using multiclass error-correcting output codes (ECOC) model
Syntax
Description
label = predict(Mdl,X,Name,Value)
[
uses any of the input argument combinations in the previous syntaxes and additionally
returns: label,NegLoss,PBScore]
= predict(___)
An array of negated average binary losses (
NegLoss). For each observation inX,predictassigns the label of the class yielding the largest negated average binary loss (or, equivalently, the smallest average binary loss).An array of positive-class scores (
PBScore) for the observations classified by each binary learner.
Examples
Load Fisher's iris data set. Specify the predictor data X, the response data Y, and the order of the classes in Y.
load fisheriris X = meas; Y = categorical(species); classOrder = unique(Y); rng(1); % For reproducibility
Train an ECOC model using SVM binary classifiers. Specify a 30% holdout sample, standardize the predictors using an SVM template, and specify the class order.
t = templateSVM('Standardize',true); PMdl = fitcecoc(X,Y,'Holdout',0.30,'Learners',t,'ClassNames',classOrder); Mdl = PMdl.Trained{1}; % Extract trained, compact classifier
PMdl is a ClassificationPartitionedECOC model. It has the property Trained, a 1-by-1 cell array containing the CompactClassificationECOC model that the software trained using the training set.
Predict the test-sample labels. Print a random subset of true and predicted labels.
testInds = test(PMdl.Partition); % Extract the test indices XTest = X(testInds,:); YTest = Y(testInds,:); labels = predict(Mdl,XTest); idx = randsample(sum(testInds),10); table(YTest(idx),labels(idx),... 'VariableNames',{'TrueLabels','PredictedLabels'})
ans=10×2 table
TrueLabels PredictedLabels
__________ _______________
setosa setosa
versicolor virginica
setosa setosa
virginica virginica
versicolor versicolor
setosa setosa
virginica virginica
virginica virginica
setosa setosa
setosa setosa
Mdl correctly labels all except one of the test-sample observations with indices idx.
Load Fisher's iris data set. Specify the predictor data X, the response data Y, and the order of the classes in Y.
load fisheriris X = meas; Y = categorical(species); classOrder = unique(Y); % Class order rng(1); % For reproducibility
Train an ECOC model using SVM binary classifiers and specify a 30% holdout sample. Standardize the predictors using an SVM template, and specify the class order.
t = templateSVM('Standardize',true); PMdl = fitcecoc(X,Y,'Holdout',0.30,'Learners',t,'ClassNames',classOrder); Mdl = PMdl.Trained{1}; % Extract trained, compact classifier
PMdl is a ClassificationPartitionedECOC model. It has the property Trained, a 1-by-1 cell array containing the CompactClassificationECOC model that the software trained using the training set.
SVM scores are signed distances from the observation to the decision boundary. Therefore, is the domain. Create a custom binary loss function that does the following:
Map the coding design matrix (M) and positive-class classification scores (s) for each learner to the binary loss for each observation.
Use linear loss.
Aggregate the binary learner loss using the median.
You can create a separate function for the binary loss function, and then save it on the MATLAB® path. Or, you can specify an anonymous binary loss function. In this case, create a function handle (customBL) to an anonymous binary loss function.
customBL = @(M,s) median(1 - (M.*s),2,'omitnan')/2;Predict test-sample labels and estimate the median binary loss per class. Print the median negative binary losses per class for a random set of 10 test-sample observations.
testInds = test(PMdl.Partition); % Extract the test indices XTest = X(testInds,:); YTest = Y(testInds,:); [label,NegLoss] = predict(Mdl,XTest,'BinaryLoss',customBL); idx = randsample(sum(testInds),10); classOrder
classOrder = 3×1 categorical
setosa
versicolor
virginica
table(YTest(idx),label(idx),NegLoss(idx,:),'VariableNames',... {'TrueLabel','PredictedLabel','NegLoss'})
ans=10×3 table
TrueLabel PredictedLabel NegLoss
__________ ______________ __________________________________
setosa versicolor 0.1858 1.9878 -3.6736
versicolor virginica -1.3315 -0.12361 -0.044843
setosa versicolor 0.13891 1.9261 -3.565
virginica virginica -1.513 -0.38284 0.39588
versicolor versicolor -0.87221 0.74738 -1.3752
setosa versicolor 0.48413 1.9976 -3.9818
virginica virginica -1.936 -0.67566 1.1117
virginica virginica -1.5786 -0.83331 0.91194
setosa versicolor 0.51027 2.1211 -4.1314
setosa versicolor 0.36128 2.0596 -3.9209
The order of the columns corresponds to the elements of classOrder. The software predicts the label based on the maximum negated loss. The results indicate that the median of the linear losses might not perform as well as other losses.
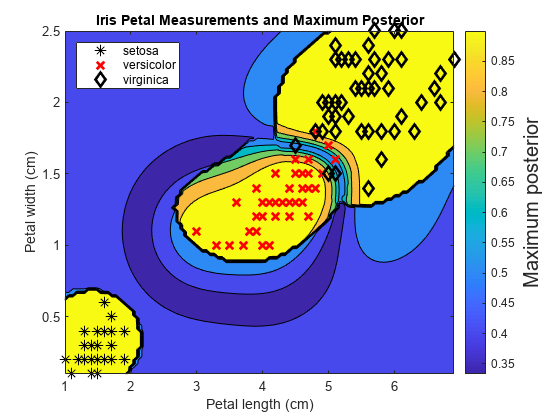
Train an ECOC classifier using SVM binary learners. First predict the training-sample labels and class posterior probabilities. Then predict the maximum class posterior probability at each point in a grid. Visualize the results.
Load Fisher's iris data set. Specify the petal dimensions as the predictors and the species names as the response.
load fisheriris X = meas(:,3:4); Y = species; rng(1); % For reproducibility
Create an SVM template. Standardize the predictors, and specify the Gaussian kernel.
t = templateSVM('Standardize',true,'KernelFunction','gaussian');
t is an SVM template. Most of its properties are empty. When the software trains the ECOC classifier, it sets the applicable properties to their default values.
Train the ECOC classifier using the SVM template. Transform classification scores to class posterior probabilities (which are returned by predict or resubPredict) using the 'FitPosterior' name-value pair argument. Specify the class order using the 'ClassNames' name-value pair argument. Display diagnostic messages during training by using the 'Verbose' name-value pair argument.
Mdl = fitcecoc(X,Y,'Learners',t,'FitPosterior',true,... 'ClassNames',{'setosa','versicolor','virginica'},... 'Verbose',2);
Training binary learner 1 (SVM) out of 3 with 50 negative and 50 positive observations. Negative class indices: 2 Positive class indices: 1 Fitting posterior probabilities for learner 1 (SVM). Training binary learner 2 (SVM) out of 3 with 50 negative and 50 positive observations. Negative class indices: 3 Positive class indices: 1 Fitting posterior probabilities for learner 2 (SVM). Training binary learner 3 (SVM) out of 3 with 50 negative and 50 positive observations. Negative class indices: 3 Positive class indices: 2 Fitting posterior probabilities for learner 3 (SVM).
Mdl is a ClassificationECOC model. The same SVM template applies to each binary learner, but you can adjust options for each binary learner by passing in a cell vector of templates.
Predict the training-sample labels and class posterior probabilities. Display diagnostic messages during the computation of labels and class posterior probabilities by using the 'Verbose' name-value pair argument.
[label,~,~,Posterior] = resubPredict(Mdl,'Verbose',1);Predictions from all learners have been computed. Loss for all observations has been computed. Computing posterior probabilities...
Mdl.BinaryLoss
ans = 'quadratic'
The software assigns an observation to the class that yields the smallest average binary loss. Because all binary learners are computing posterior probabilities, the binary loss function is quadratic.
Display a random set of results.
idx = randsample(size(X,1),10,1); Mdl.ClassNames
ans = 3×1 cell
{'setosa' }
{'versicolor'}
{'virginica' }
table(Y(idx),label(idx),Posterior(idx,:),... 'VariableNames',{'TrueLabel','PredLabel','Posterior'})
ans=10×3 table
TrueLabel PredLabel Posterior
______________ ______________ ______________________________________
{'virginica' } {'virginica' } 0.0039322 0.003987 0.99208
{'virginica' } {'virginica' } 0.017067 0.018263 0.96467
{'virginica' } {'virginica' } 0.014948 0.015856 0.9692
{'versicolor'} {'versicolor'} 2.2197e-14 0.87318 0.12682
{'setosa' } {'setosa' } 0.999 0.00025092 0.00074638
{'versicolor'} {'virginica' } 2.2195e-14 0.05943 0.94057
{'versicolor'} {'versicolor'} 2.2194e-14 0.97001 0.029985
{'setosa' } {'setosa' } 0.999 0.00024991 0.0007474
{'versicolor'} {'versicolor'} 0.0085642 0.98259 0.0088487
{'setosa' } {'setosa' } 0.999 0.00025013 0.00074717
The columns of Posterior correspond to the class order of Mdl.ClassNames.
Define a grid of values in the observed predictor space. Predict the posterior probabilities for each instance in the grid.
xMax = max(X); xMin = min(X); x1Pts = linspace(xMin(1),xMax(1)); x2Pts = linspace(xMin(2),xMax(2)); [x1Grid,x2Grid] = meshgrid(x1Pts,x2Pts); [~,~,~,PosteriorRegion] = predict(Mdl,[x1Grid(:),x2Grid(:)]);
For each coordinate on the grid, plot the maximum class posterior probability among all classes.
contourf(x1Grid,x2Grid,... reshape(max(PosteriorRegion,[],2),size(x1Grid,1),size(x1Grid,2))); h = colorbar; h.YLabel.String = 'Maximum posterior'; h.YLabel.FontSize = 15; hold on gh = gscatter(X(:,1),X(:,2),Y,'krk','*xd',8); gh(2).LineWidth = 2; gh(3).LineWidth = 2; title('Iris Petal Measurements and Maximum Posterior') xlabel('Petal length (cm)') ylabel('Petal width (cm)') axis tight legend(gh,'Location','NorthWest') hold off
Train a multiclass ECOC model and estimate posterior probabilities using parallel computing.
Load the arrhythmia data set. Examine the response data Y, and determine the number of classes.
load arrhythmia
Y = categorical(Y);
tabulate(Y) Value Count Percent
1 245 54.20%
2 44 9.73%
3 15 3.32%
4 15 3.32%
5 13 2.88%
6 25 5.53%
7 3 0.66%
8 2 0.44%
9 9 1.99%
10 50 11.06%
14 4 0.88%
15 5 1.11%
16 22 4.87%
K = numel(unique(Y));
Several classes are not represented in the data, and many of the other classes have low relative frequencies.
Specify an ensemble learning template that uses the GentleBoost method and 50 weak classification tree learners.
t = templateEnsemble('GentleBoost',50,'Tree');
t is a template object. Most of its properties are empty ([]). The software uses default values for all empty properties during training.
Because the response variable contains many classes, specify a sparse random coding design.
rng(1); % For reproducibility Coding = designecoc(K,'sparserandom');
Train an ECOC model using parallel computing. Specify a 15% holdout sample, and fit posterior probabilities.
pool = parpool; % Invokes workersStarting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 6).
options = statset('UseParallel',true); PMdl = fitcecoc(X,Y,'Learner',t,'Options',options,'Coding',Coding,... 'FitPosterior',true,'Holdout',0.15); Mdl = PMdl.Trained{1}; % Extract trained, compact classifier
PMdl is a ClassificationPartitionedECOC model. It has the property Trained, a 1-by-1 cell array containing the CompactClassificationECOC model that the software trained using the training set.
The pool invokes six workers, although the number of workers might vary among systems.
Estimate posterior probabilities, and display the posterior probability of being classified as not having arrhythmia (class 1) given the data for a random set of test-sample observations.
testInds = test(PMdl.Partition); % Extract the test indices XTest = X(testInds,:); YTest = Y(testInds,:); [~,~,~,posterior] = predict(Mdl,XTest,'Options',options); idx = randsample(sum(testInds),10); table(idx,YTest(idx),posterior(idx,1),... 'VariableNames',{'TestSampleIndex','TrueLabel','PosteriorNoArrhythmia'})
ans=10×3 table
TestSampleIndex TrueLabel PosteriorNoArrhythmia
_______________ _________ _____________________
11 6 0.60631
41 4 0.23674
51 2 0.13802
33 10 0.43831
12 1 0.94332
8 1 0.97278
37 1 0.62807
24 10 0.96876
56 16 0.29375
30 1 0.64512
Input Arguments
Full or compact multiclass ECOC model, specified as a
ClassificationECOC or
CompactClassificationECOC model
object.
To create a full or compact ECOC model, see ClassificationECOC or CompactClassificationECOC.
Predictor data to be classified, specified as a numeric matrix or table.
By default, each row of X corresponds to one observation, and
each column corresponds to one variable.
For a numeric matrix:
The variables that constitute the columns of
Xmust have the same order as the predictor variables that trainMdl.If you train
Mdlusing a table (for example,Tbl), thenXcan be a numeric matrix ifTblcontains all numeric predictor variables. To treat numeric predictors inTblas categorical during training, identify categorical predictors using theCategoricalPredictorsname-value pair argument offitcecoc. IfTblcontains heterogeneous predictor variables (for example, numeric and categorical data types) andXis a numeric matrix, thenpredictthrows an error.
For a table:
predictdoes not support multicolumn variables or cell arrays other than cell arrays of character vectors.If you train
Mdlusing a table (for example,Tbl), then all predictor variables inXmust have the same variable names and data types as the predictor variables that trainMdl(stored inMdl.PredictorNames). However, the column order ofXdoes not need to correspond to the column order ofTbl. BothTblandXcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.If you train
Mdlusing a numeric matrix, then the predictor names inMdl.PredictorNamesand the corresponding predictor variable names inXmust be the same. To specify predictor names during training, see thePredictorNamesname-value pair argument offitcecoc. All predictor variables inXmust be numeric vectors.Xcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.
Note
If Mdl.BinaryLearners contains linear classification models
(ClassificationLinear), then you can orient
your predictor matrix so that observations correspond to columns and specify
'ObservationsIn','columns'. However, you cannot specify
'ObservationsIn','columns' for predictor data in a table.
When training Mdl, assume that you set
'Standardize',true for a template object specified in the
'Learners' name-value pair argument of fitcecoc. In
this case, for the corresponding binary learner j, the software standardizes
the columns of the new predictor data using the corresponding means in
Mdl.BinaryLearner{j}.Mu and standard deviations in
Mdl.BinaryLearner{j}.Sigma.
Data Types: table | double | single
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: predict(Mdl,X,'BinaryLoss','quadratic','Decoding','lossbased')
specifies a quadratic binary learner loss function and a loss-based decoding scheme for
aggregating the binary losses.
Binary learner loss function, specified as a built-in loss function name or function handle.
This table describes the built-in functions, where yj is the class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes binary losses so that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class [1].
For a custom binary loss function, for example
customFunction, specify its function handleBinaryLoss=@customFunction.customFunctionhas this form:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of passing a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function.
This table identifies the default BinaryLoss value, which depends on the
score ranges returned by the binary learners.
| Assumption | Default Value |
|---|---|
All binary learners are any of the following:
| "quadratic" |
| All binary learners are SVMs or linear or kernel classification models of SVM learners. | "hinge" |
All binary learners are ensembles trained by
AdaboostM1 or
GentleBoost. | "exponential" |
All binary learners are ensembles trained by
LogitBoost. | "binodeviance" |
You specify to predict class posterior probabilities by setting
FitPosterior=true in fitcecoc. | "quadratic" |
| Binary learners are heterogeneous and use different loss functions. | "hamming" |
To check the default value, use dot notation to display the BinaryLoss property of the trained model at the command line.
Example: BinaryLoss="binodeviance"
Data Types: char | string | function_handle
Decoding scheme that aggregates the binary losses, specified as
"lossweighted" or "lossbased". For more
information, see Binary Loss.
Example: Decoding="lossbased"
Data Types: char | string
Number of random initial values for fitting posterior probabilities by Kullback-Leibler
divergence minimization, specified as the comma-separated pair consisting of
'NumKLInitializations' and a nonnegative integer scalar.
If you do not request the fourth output argument (Posterior) and set
'PosteriorMethod','kl' (the default), then the software ignores
the value of NumKLInitializations.
For more details, see Posterior Estimation Using Kullback-Leibler Divergence.
Example: 'NumKLInitializations',5
Data Types: single | double
Predictor data observation dimension, specified as the comma-separated pair consisting of
'ObservationsIn' and 'columns' or
'rows'. Mdl.BinaryLearners must contain
ClassificationLinear models.
Note
If you orient your predictor matrix so that
observations correspond to columns and specify
'ObservationsIn','columns', you
can experience a significant reduction in
execution time. You cannot specify
'ObservationsIn','columns' for
predictor data in a table.
Estimation options, specified as a structure array as returned by statset.
To invoke parallel computing you need a Parallel Computing Toolbox™ license.
Example: Options=statset(UseParallel=true)
Data Types: struct
Posterior probability estimation method, specified as the comma-separated
pair consisting of 'PosteriorMethod' and 'kl' or 'qp'.
If
PosteriorMethodis'kl', then the software estimates multiclass posterior probabilities by minimizing the Kullback-Leibler divergence between the predicted and expected posterior probabilities returned by binary learners. For details, see Posterior Estimation Using Kullback-Leibler Divergence.If
PosteriorMethodis'qp', then the software estimates multiclass posterior probabilities by solving a least-squares problem using quadratic programming. You need an Optimization Toolbox™ license to use this option. For details, see Posterior Estimation Using Quadratic Programming.If you do not request the fourth output argument (
Posterior), then the software ignores the value ofPosteriorMethod.
Example: 'PosteriorMethod','qp'
Verbosity level, specified as 0 or 1.
Verbose controls the number of diagnostic messages that the
software displays in the Command Window.
If Verbose is 0, then the software does not display
diagnostic messages. Otherwise, the software displays diagnostic messages.
Example: Verbose=1
Data Types: single | double
Output Arguments
Predicted class labels, returned as a categorical, character, logical, or numeric array, or a cell array of character vectors.
The predict function predicts the
classification of an observation by assigning the observation to the class yielding the largest
negated average binary loss (or, equivalently, the smallest average binary loss). For an
observation with NaN loss values, the function classifies the observation
into the majority class, which makes up the largest proportion of the training labels.
label has the same data type as the class labels used to train
Mdl and has the same number of rows as X.
(The software treats string arrays as cell arrays of character
vectors.)
If Mdl.BinaryLearners contains ClassificationLinear models, then label is an
m-by-L matrix, where m is the
number of observations in X, and L is the number
of regularization strengths in the linear classification models
(numel(Mdl.BinaryLearners{1}.Lambda)). The value
label(i,j) is the predicted label of observation
i for the model trained using regularization strength
Mdl.BinaryLearners{1}.Lambda(j).
Otherwise, label is a column vector of length
m.
Negated average binary losses, returned as a numeric matrix or array.
If
Mdl.BinaryLearnerscontainsClassificationLinearmodels, thenNegLossis an m-by-K-by-L array.m is the number of observations in
X.K is the number of distinct classes in the training data (
numel(Mdl.ClassNames)).L is the number of regularization strengths in the linear classification models (
numel(Mdl.BinaryLearners{1}.Lambda)).
NegLoss(i,k,j)is the negated average binary loss for observationi, corresponding to classMdl.ClassNames(k), for the model trained using regularization strengthMdl.BinaryLearners{1}.Lambda(j).If
Decodingis'lossbased', thenNegLoss(i,k,j)is the sum of the binary losses divided by the total number of binary learners.If
Decodingis'lossweighted', thenNegLoss(i,k,j)is the sum of the binary losses divided by the number of binary learners for the kth class.
For more details, see Binary Loss.
Otherwise,
NegLossis an m-by-K matrix.
Positive-class scores for each binary learner, returned as a numeric matrix or array.
If
Mdl.BinaryLearnerscontainsClassificationLinearmodels, thenPBScoreis an m-by-B-by-L array.m is the number of observations in
X.B is the number of binary learners (
numel(Mdl.BinaryLearners)).L is the number of regularization strengths in the linear classification models (
numel(Mdl.BinaryLearners{1}.Lambda)).
PBScore(i,b,j)is the positive-class score for observationi, using binary learnerb, for the model trained using regularization strengthMdl.BinaryLearners{1}.Lambda(j).Otherwise,
PBScoreis an m-by-B matrix.
Posterior class probabilities, returned as a numeric matrix or array.
If
Mdl.BinaryLearnerscontainsClassificationLinearmodels, thenPosterioris an m-by-K-by-L array. For dimension definitions, seeNegLoss.Posterior(i,k,j)is the posterior probability that observationicomes from classMdl.ClassNames(k), for the model trained using regularization strengthMdl.BinaryLearners{1}.Lambda(j).Otherwise,
Posterioris an m-by-K matrix.
More About
The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [3] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [4] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the loss and
predict object functions), which measures how well an ECOC classifier
performs as a whole.
Algorithms
The software can estimate class posterior probabilities by minimizing the Kullback-Leibler divergence or by using quadratic programming. For the following descriptions of the posterior estimation algorithms, assume that:
mkj is the element (k,j) of the coding design matrix M.
I is the indicator function.
is the class posterior probability estimate for class k of an observation, k = 1,...,K.
rj is the positive-class posterior probability for binary learner j. That is, rj is the probability that binary learner j classifies an observation into the positive class, given the training data.
By default, the software minimizes the Kullback-Leibler divergence to estimate class posterior probabilities. The Kullback-Leibler divergence between the expected and observed positive-class posterior probabilities is
where is the weight for binary learner j.
Sj is the set of observation indices on which binary learner j is trained.
is the weight of observation i.
The software minimizes the divergence iteratively. The first step is to choose initial values for the class posterior probabilities.
If you do not specify
'NumKLIterations', then the software tries both sets of deterministic initial values described next, and selects the set that minimizes Δ.is the solution of the system
where M01 is M with all mkj = –1 replaced with 0, and r is a vector of positive-class posterior probabilities returned by the L binary learners [Dietterich et al.]. The software uses
lsqnonnegto solve the system.
If you specify
'NumKLIterations',c, wherecis a natural number, then the software does the following to choose the set , and selects the set that minimizes Δ.The software tries both sets of deterministic initial values as described previously.
The software randomly generates
cvectors of length K usingrand, and then normalizes each vector to sum to 1.
At iteration t, the software completes these steps:
Compute
Estimate the next class posterior probability using
Normalize so that they sum to 1.
Check for convergence.
For more details, see [Hastie et al.] and [Zadrozny].
Posterior probability estimation using quadratic programming requires an Optimization Toolbox license. To estimate posterior probabilities for an observation using this method, the software completes these steps:
Estimate the positive-class posterior probabilities, rj, for binary learners j = 1,...,L.
Using the relationship between rj and [Wu et al.], minimize
with respect to and the restrictions
The software performs minimization using
quadprog(Optimization Toolbox).
Alternative Functionality
Simulink Block
To integrate the prediction of an ECOC classification model into Simulink®, you can use the ClassificationECOC
Predict block in the Statistics and Machine Learning Toolbox™ library or a MATLAB® Function block with the predict function. For examples,
see Predict Class Labels Using ClassificationECOC Predict Block and Predict Class Labels Using MATLAB Function Block.
When deciding which approach to use, consider the following:
If you use the Statistics and Machine Learning Toolbox library block, you can use the Fixed-Point Tool (Fixed-Point Designer) to convert a floating-point model to fixed point.
Support for variable-size arrays must be enabled for a MATLAB Function block with the
predictfunction.If you use a MATLAB Function block, you can use MATLAB functions for preprocessing or post-processing before or after predictions in the same MATLAB Function block.
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Dietterich, T., and G. Bakiri. “Solving Multiclass Learning Problems Via Error-Correcting Output Codes.” Journal of Artificial Intelligence Research. Vol. 2, 1995, pp. 263–286.
[3] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[4] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
[5] Hastie, T., and R. Tibshirani. “Classification by Pairwise Coupling.” Annals of Statistics. Vol. 26, Issue 2, 1998, pp. 451–471.
[6] Wu, T. F., C. J. Lin, and R. Weng. “Probability Estimates for Multi-Class Classification by Pairwise Coupling.” Journal of Machine Learning Research. Vol. 5, 2004, pp. 975–1005.
[7] Zadrozny, B. “Reducing Multiclass to Binary by Coupling Probability Estimates.” NIPS 2001: Proceedings of Advances in Neural Information Processing Systems 14, 2001, pp. 1041–1048.
Extended Capabilities
The
predict function supports tall arrays with the following usage
notes and limitations:
predictdoes not support talltabledata whenMdlcontains kernel or linear binary learners.
For more information, see Tall Arrays.
Usage notes and limitations:
You can generate C/C++ code for both
predictandupdateby using a coder configurer. Or, generate code only forpredictby usingsaveLearnerForCoder,loadLearnerForCoder, andcodegen.Code generation for
predictandupdate— Create a coder configurer by usinglearnerCoderConfigurerand then generate code by usinggenerateCode. Then you can update model parameters in the generated code without having to regenerate the code.Code generation for
predict— Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls thepredictfunction. Then usecodegen(MATLAB Coder) to generate code for the entry-point function.
To generate single-precision C/C++ code for
predict, specifyDataType="single"when you call theloadLearnerForCoderfunction.This table contains notes about the arguments of
predict. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlIf you use
saveLearnerForCoderto save a model that is equipped to predict posterior probabilities, and useloadLearnerForCoderto load the model, thenloadLearnerForCodercannot restore theScoreTransformproperty into the MATLAB Workspace. However,loadLearnerForCodercan load the model, including theScoreTransformproperty, within an entry-point function at compile time for code generation.For the usage notes and limitations of the model object, see Code Generation of the
CompactClassificationECOCobject.
XFor general code generation,
Xmust be a single-precision or double-precision matrix or a table containing numeric variables, categorical variables, or both.In the coder configurer workflow,
Xmust be a single-precision or double-precision matrix.The number of observations in
Xcan be a variable size, but the number of variables inXmust be fixed.If you want to specify
Xas a table, then your model must be trained using a table, and your entry-point function for prediction must do the following:Accept data as arrays.
Create a table from the data input arguments and specify the variable names in the table.
Pass the table to
predict.
For an example of this table workflow, see Generate Code to Classify Data in Table. For more information on using tables in code generation, see Code Generation for Tables (MATLAB Coder) and Table Limitations for Code Generation (MATLAB Coder).
PosteriorThis output argument is not supported. Name-value pair arguments Names in name-value arguments must be compile-time constants. BinaryLossThe value for the
'BinaryLoss'name-value pair argument must be a compile-time constant. For example, to use the'BinaryLoss','logit'name-value pair argument in the generated code, include{coder.Constant('BinaryLoss'),coder.Constant('logit')}in the-argsvalue ofcodegen(MATLAB Coder).To set the
'BinaryLoss'name-value pair argument to a custom binary loss function in the generated code, define a custom function on the MATLAB search path, and specify the name of the custom function instead of its function handle. The custom function name must be a compile-time constant. For example, if you define a custom function namedcustomFunction, then include{coder.Constant('BinaryLoss'),coder.Constant('customFunction')}in the-argsvalue ofcodegen(MATLAB Coder).
NumKLInitializationsThis name-value pair argument is not supported. ObservationsInThe value for the
ObservationsInname-value argument must be a compile-time constant. For example, to use the"ObservationsIn","columns"name-value argument in the generated code, include{coder.Constant("ObservationsIn"),coder.Constant("columns")}in the-argsvalue ofcodegen(MATLAB Coder).OptionsThis name-value pair argument is not supported. PosteriorMethodThis name-value pair argument is not supported. VerboseIf you plan to generate a MEX file without using a coder configurer, then you can specify Verbose. Otherwise,codegendoes not supportVerbose.
For more information, see Introduction to Code Generation.
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Usage notes and limitations:
The
predictfunction does not support models trained using:Decision tree learners with surrogate splits
SVM learners for one-class classification
KNN learners that use the Kd-tree nearest neighbor search method, function handle distance metrics, or tie inclusion
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2014b
See Also
CompactClassificationECOC | ClassificationECOC | fitcecoc | statset | resubPredict | quadprog (Optimization Toolbox) | loss
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)