fitcsvm
Train support vector machine (SVM) classifier for one-class and binary classification
Syntax
Description
fitcsvm trains or cross-validates a support vector
machine (SVM) model for one-class and two-class (binary) classification on a
low-dimensional or moderate-dimensional predictor data set. fitcsvm
supports mapping the predictor data using kernel functions, and supports sequential
minimal optimization (SMO), iterative single data algorithm (ISDA), or
L1 soft-margin minimization via quadratic programming for
objective-function minimization.
To train a linear SVM model for binary classification on a high-dimensional data set,
that is, a data set that includes many predictor variables, use fitclinear instead.
For multiclass learning with combined binary SVM models, use error-correcting output
codes (ECOC). For more details, see fitcecoc.
To train an SVM regression model, see fitrsvm for low-dimensional and moderate-dimensional predictor data
sets, or fitrlinear for high-dimensional data
sets.
Mdl = fitcsvm(Tbl,ResponseVarName)Mdl trained using the sample data contained in the table
Tbl. ResponseVarName is the name of
the variable in Tbl that contains the class labels for
one-class or two-class classification.
If the class label variable contains only one class (for example, a vector of
ones), fitcsvm trains a model for one-class classification.
Otherwise, the function trains a model for two-class classification.
Mdl = fitcsvm(___,Name,Value)
[
also returns Mdl,AggregateOptimizationResults] = fitcsvm(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments.
You must also specify the ConstraintType and
ConstraintBounds options of
HyperparameterOptimizationOptions. You can use this
syntax to optimize on compact model size instead of cross-validation loss, and
to perform a set of multiple optimization problems that have the same options
but different constraint bounds.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
fitcsvmtrains SVM classifiers for one-class or two-class learning applications. To train SVM classifiers using data with more than two classes, usefitcecoc.fitcsvmsupports low-dimensional and moderate-dimensional data sets. For high-dimensional data sets, usefitclinearinstead.
More About
Tips
Unless your data set is large, always try to standardize the predictors (see
Standardize). Standardization makes predictors insensitive to the scales on which they are measured.It is a good practice to cross-validate using the
KFoldname-value pair argument. The cross-validation results determine how well the SVM classifier generalizes.For one-class learning:
The default setting for the name-value pair argument
Alphacan lead to long training times. To speed up training, setAlphato a vector mostly composed of0s.Set the name-value pair argument
Nuto a value closer to0to yield fewer support vectors and, therefore, a smoother but crude decision boundary.
Sparsity in support vectors is a desirable property of an SVM classifier. To decrease the number of support vectors, set
BoxConstraintto a large value. This action increases the training time.For optimal training time, set
CacheSizeas high as the memory limit your computer allows.If you expect many fewer support vectors than observations in the training set, then you can significantly speed up convergence by shrinking the active set using the name-value pair argument
'ShrinkagePeriod'. It is a good practice to specify'ShrinkagePeriod',1000.Duplicate observations that are far from the decision boundary do not affect convergence. However, just a few duplicate observations that occur near the decision boundary can slow down convergence considerably. To speed up convergence, specify
'RemoveDuplicates',trueif:Your data set contains many duplicate observations.
You suspect that a few duplicate observations fall near the decision boundary.
To maintain the original data set during training,
fitcsvmmust temporarily store separate data sets: the original and one without the duplicate observations. Therefore, if you specifytruefor data sets containing few duplicates, thenfitcsvmconsumes close to double the memory of the original data.After training a model, you can generate C/C++ code that predicts labels for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
For the mathematical formulation of the SVM binary classification algorithm, see Support Vector Machines for Binary Classification and Understanding Support Vector Machines.
NaN,<undefined>, empty character vector (''), empty string (""), and<missing>values indicate missing values.fitcsvmremoves entire rows of data corresponding to a missing response. When computing total weights (see the next bullets),fitcsvmignores any weight corresponding to an observation with at least one missing predictor. This action can lead to unbalanced prior probabilities in balanced-class problems. Consequently, observation box constraints might not equalBoxConstraint.If you specify the
Cost,Prior, andWeightsname-value arguments, the output model object stores the specified values in theCost,Prior, andWproperties, respectively. TheCostproperty stores the user-specified cost matrix (C) without modification. ThePriorandWproperties store the prior probabilities and observation weights, respectively, after normalization. For model training, the software updates the prior probabilities and observation weights to incorporate the penalties described in the cost matrix. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.Note that the
CostandPriorname-value arguments are used for two-class learning. For one-class learning, theCostandPriorproperties store0and1, respectively.For two-class learning,
fitcsvmassigns a box constraint to each observation in the training data. The formula for the box constraint of observation j iswhere C0 is the initial box constraint (see the
BoxConstraintname-value argument), and wj* is the observation weight adjusted byCostandPriorfor observation j. For details about the observation weights, see Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix.If you specify
Standardizeastrueand set theCost,Prior, orWeightsname-value argument, thenfitcsvmstandardizes the predictors using their corresponding weighted means and weighted standard deviations. That is,fitcsvmstandardizes predictor j (xj) usingwhere xjk is observation k (row) of predictor j (column), and
Assume that
pis the proportion of outliers that you expect in the training data, and that you set'OutlierFraction',p.For one-class learning, the software trains the bias term such that 100
p% of the observations in the training data have negative scores.The software implements robust learning for two-class learning. In other words, the software attempts to remove 100
p% of the observations when the optimization algorithm converges. The removed observations correspond to gradients that are large in magnitude.
If your predictor data contains categorical variables, then the software generally uses full dummy encoding for these variables. The software creates one dummy variable for each level of each categorical variable.
The
PredictorNamesproperty stores one element for each of the original predictor variable names. For example, assume that there are three predictors, one of which is a categorical variable with three levels. ThenPredictorNamesis a 1-by-3 cell array of character vectors containing the original names of the predictor variables.The
ExpandedPredictorNamesproperty stores one element for each of the predictor variables, including the dummy variables. For example, assume that there are three predictors, one of which is a categorical variable with three levels. ThenExpandedPredictorNamesis a 1-by-5 cell array of character vectors containing the names of the predictor variables and the new dummy variables.Similarly, the
Betaproperty stores one beta coefficient for each predictor, including the dummy variables.The
SupportVectorsproperty stores the predictor values for the support vectors, including the dummy variables. For example, assume that there are m support vectors and three predictors, one of which is a categorical variable with three levels. ThenSupportVectorsis an n-by-5 matrix.The
Xproperty stores the training data as originally input and does not include the dummy variables. When the input is a table,Xcontains only the columns used as predictors.
For predictors specified in a table, if any of the variables contain ordered (ordinal) categories, the software uses ordinal encoding for these variables.
For a variable with k ordered levels, the software creates k – 1 dummy variables. The jth dummy variable is –1 for levels up to j, and +1 for levels j + 1 through k.
The names of the dummy variables stored in the
ExpandedPredictorNamesproperty indicate the first level with the value +1. The software stores k – 1 additional predictor names for the dummy variables, including the names of levels 2, 3, ..., k.
All solvers implement L1 soft-margin minimization.
For one-class learning, the software estimates the Lagrange multipliers, α1,...,αn, such that
Alternative Functionality
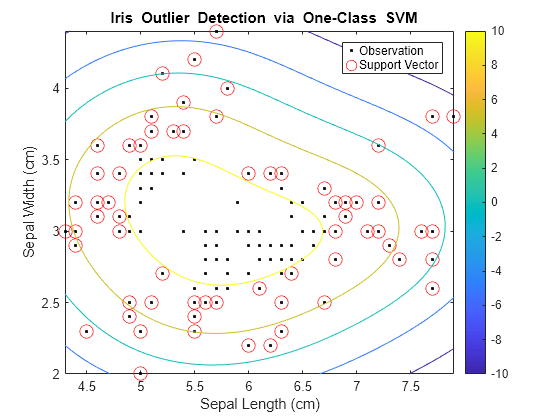
You can also use the ocsvm
function to train a one-class SVM model for anomaly detection.
The
ocsvmfunction provides a simpler and preferred workflow for anomaly detection than thefitcsvmfunction.The
ocsvmfunction returns aOneClassSVMobject, anomaly indicators, and anomaly scores. You can use the outputs to identify anomalies in training data. To find anomalies in new data, you can use theisanomalyobject function ofOneClassSVM. Theisanomalyfunction returns anomaly indicators and scores for the new data.The
fitcsvmfunction supports both one-class and binary classification. If the class label variable contains only one class (for example, a vector of ones),fitcsvmtrains a model for one-class classification and returns aClassificationSVMobject. To identify anomalies, you must first compute anomaly scores by using theresubPredictorpredictobject function ofClassificationSVM, and then identify anomalies by finding observations that have negative scores.Note that a large positive anomaly score indicates an anomaly in
ocsvm, whereas a negative score indicates an anomaly inpredictofClassificationSVM.
The
ocsvmfunction finds the decision boundary based on the primal form of SVM, whereas thefitcsvmfunction finds the decision boundary based on the dual form of SVM.The solver in
ocsvmis computationally less expensive than the solver infitcsvmfor a large data set (large n). Unlike solvers infitcsvm, which require computation of the n-by-n Gram matrix, the solver inocsvmonly needs to form a matrix of size n-by-m. Here, m is the number of dimensions of expanded space, which is typically much less than n for big data.
References
Extended Capabilities
Version History
Introduced in R2014aSee Also
ClassificationSVM | CompactClassificationSVM | ClassificationPartitionedModel | predict | fitSVMPosterior | rng | quadprog (Optimization Toolbox) | fitcecoc | fitclinear | ocsvm