Support Vector Machines for Binary Classification
Understanding Support Vector Machines
Separable Data
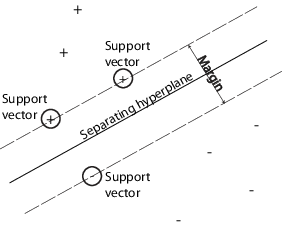
You can use a support vector machine (SVM) when your data has exactly two classes. An SVM classifies data by finding the best hyperplane that separates all data points of one class from those of the other class. The best hyperplane for an SVM means the one with the largest margin between the two classes. Margin means the maximal width of the slab parallel to the hyperplane that has no interior data points.
The support vectors are the data points that are closest to the separating hyperplane; these points are on the boundary of the slab. The following figure illustrates these definitions, with + indicating data points of type 1, and – indicating data points of type –1.
Mathematical Formulation: Primal. This discussion follows Hastie, Tibshirani, and Friedman [1] and Christianini and Shawe-Taylor [2].
The data for training is a set of points (vectors) xj along with their categories yj. For some dimension d, the xj ∊ Rd, and the yj = ±1. The equation of a hyperplane is
where β ∊ Rd and b is a real number.
The following problem defines the best separating hyperplane (i.e., the decision boundary). Find β and b that minimize ||β|| such that for all data points (xj,yj),
The support vectors are the xj on the boundary, those for which
For mathematical convenience, the problem is usually given as the equivalent problem of minimizing . This is a quadratic programming problem. The optimal solution enables classification of a vector z as follows:
is the classification score and represents the distance z is from the decision boundary.
Mathematical Formulation: Dual. It is computationally simpler to solve the dual quadratic programming problem. To obtain the dual, take positive Lagrange multipliers αj multiplied by each constraint, and subtract from the objective function:
where you look for a stationary point of LP over β and b. Setting the gradient of LP to 0, you get
| (1) |
Substituting into LP, you get the dual LD:
which you maximize over αj ≥ 0. In general, many αj are 0 at the maximum. The nonzero αj in the solution to the dual problem define the hyperplane, as seen in Equation 1, which gives β as the sum of αjyjxj. The data points xj corresponding to nonzero αj are the support vectors.
The derivative of LD with respect to a nonzero αj is 0 at an optimum. This gives
In particular, this gives the value of b at the solution, by taking any j with nonzero αj.
The dual is a standard quadratic programming problem. For example, the
Optimization Toolbox™
quadprog (Optimization Toolbox) solver solves this
type of problem.
Nonseparable Data
Your data might not allow for a separating hyperplane. In that case, SVM can use a soft margin, meaning a hyperplane that separates many, but not all data points.
There are two standard formulations of soft margins. Both involve adding slack variables ξj and a penalty parameter C.
The L1-norm problem is:
such that
The L1-norm refers to using ξj as slack variables instead of their squares. The three solver options
SMO,ISDA, andL1QPoffitcsvmminimize the L1-norm problem.The L2-norm problem is:
subject to the same constraints.
In these formulations, you can see that increasing C places more weight on the slack variables ξj, meaning the optimization attempts to make a stricter separation between classes. Equivalently, reducing C towards 0 makes misclassification less important.
Mathematical Formulation: Dual. For easier calculations, consider the L1 dual problem to this soft-margin formulation. Using Lagrange multipliers μj, the function to minimize for the L1-norm problem is:
where you look for a stationary point of LP over β, b, and positive ξj. Setting the gradient of LP to 0, you get
These equations lead directly to the dual formulation:
subject to the constraints
The final set of inequalities, 0 ≤ αj ≤ C, shows why C is sometimes called a box constraint. C keeps the allowable values of the Lagrange multipliers αj in a “box”, a bounded region.
The gradient equation for b gives the solution b in terms of the set of nonzero αj, which correspond to the support vectors.
You can write and solve the dual of the L2-norm problem in an analogous manner. For details, see Christianini and Shawe-Taylor [2], Chapter 6.
fitcsvm Implementation. Both dual soft-margin problems are quadratic programming problems.
Internally, fitcsvm has several different
algorithms for solving the problems.
For one-class or binary classification, if you do not set a fraction of expected outliers in the data (see
OutlierFraction), then the default solver is Sequential Minimal Optimization (SMO). SMO minimizes the one-norm problem by a series of two-point minimizations. During optimization, SMO respects the linear constraint and explicitly includes the bias term in the model. SMO is relatively fast. For more details on SMO, see [3].For binary classification, if you set a fraction of expected outliers in the data, then the default solver is the Iterative Single Data Algorithm. Like SMO, ISDA solves the one-norm problem. Unlike SMO, ISDA minimizes by a series on one-point minimizations, does not respect the linear constraint, and does not explicitly include the bias term in the model. For more details on ISDA, see [4].
For one-class or binary classification, and if you have an Optimization Toolbox license, you can choose to use
quadprog(Optimization Toolbox) to solve the one-norm problem.quadproguses a good deal of memory, but solves quadratic programs to a high degree of precision. For more details, see Quadratic Programming Definition (Optimization Toolbox).
Nonlinear Transformation with Kernels
Some binary classification problems do not have a simple hyperplane as a useful separating criterion. For those problems, there is a variant of the mathematical approach that retains nearly all the simplicity of an SVM separating hyperplane.
This approach uses these results from the theory of reproducing kernels:
There is a class of functions G(x1,x2) with the following property. There is a linear space S and a function φ mapping x to S such that
G(x1,x2) = <φ(x1),φ(x2)>. (2) The dot product takes place in the space S.
This class of functions includes:
Polynomials: For some positive integer p,
G(x1,x2) = (1 + x1′x2)p. (3) Radial basis function (Gaussian):
G(x1,x2) = exp(–∥x1–x2∥2). (4) Multilayer perceptron or sigmoid (neural network): For a positive number p1 and a negative number p2,
G(x1,x2) = tanh(p1x1′x2 + p2). (5) Note
Not every set of p1 and p2 yields a valid reproducing kernel.
fitcsvmdoes not support the sigmoid kernel. Instead, you can define the sigmoid kernel and specify it by using the'KernelFunction'name-value pair argument. For details, see Train SVM Classifier Using Custom Kernel.
The mathematical approach using kernels relies on the computational method of hyperplanes. All the calculations for hyperplane classification use nothing more than dot products. Therefore, nonlinear kernels can use identical calculations and solution algorithms, and obtain classifiers that are nonlinear. The resulting classifiers are hypersurfaces in some space S, but the space S does not have to be identified or examined.
Using Support Vector Machines
As with any supervised learning model, you first train a support vector machine, and then cross validate the classifier. Use the trained machine to classify (predict) new data. In addition, to obtain satisfactory predictive accuracy, you can use various SVM kernel functions, and you must tune the parameters of the kernel functions.
Training an SVM Classifier
Train, and optionally cross validate, an SVM classifier using fitcsvm. The most common syntax
is:
SVMModel = fitcsvm(X,Y,'KernelFunction','rbf',...
'Standardize',true,'ClassNames',{'negClass','posClass'});The inputs are:
X— Matrix of predictor data, where each row is one observation, and each column is one predictor.Y— Array of class labels with each row corresponding to the value of the corresponding row inX.Ycan be a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors.KernelFunction— The default value is'linear'for two-class learning, which separates the data by a hyperplane. The value'gaussian'(or'rbf') is the default for one-class learning, and specifies to use the Gaussian (or radial basis function) kernel. An important step to successfully train an SVM classifier is to choose an appropriate kernel function.Standardize— Flag indicating whether the software should standardize the predictors before training the classifier.ClassNames— Distinguishes between the negative and positive classes, or specifies which classes to include in the data. The negative class is the first element (or row of a character array), e.g.,'negClass', and the positive class is the second element (or row of a character array), e.g.,'posClass'.ClassNamesmust be the same data type asY. It is good practice to specify the class names, especially if you are comparing the performance of different classifiers.
The resulting, trained model (SVMModel) contains the
optimized parameters from the SVM algorithm, enabling you to classify new
data.
For more name-value pairs you can use to control the training, see the
fitcsvm reference page.
Classifying New Data with an SVM Classifier
Classify new data using predict. The syntax for classifying
new data using a trained SVM classifier (SVMModel) is:
[label,score] = predict(SVMModel,newX);
The resulting vector, label, represents the classification
of each row in X. score is an
n-by-2 matrix of soft scores. Each row corresponds to a
row in X, which is a new observation. The first column
contains the scores for the observations being classified in the negative class,
and the second column contains the scores observations being classified in the
positive class.
To estimate posterior probabilities rather than scores, first pass the
trained SVM classifier (SVMModel) to fitPosterior, which
fits a score-to-posterior-probability transformation function to the scores. The
syntax is:
ScoreSVMModel = fitPosterior(SVMModel,X,Y);
The property ScoreTransform of the classifier
ScoreSVMModel contains the optimal transformation
function. Pass ScoreSVMModel to predict.
Rather than returning the scores, the output argument score
contains the posterior probabilities of an observation being classified in the
negative (column 1 of score) or positive (column 2 of
score) class.
Tuning an SVM Classifier
Use the 'OptimizeHyperparameters' name-value pair argument of
fitcsvm to find parameter values that minimize the
cross-validation loss. The eligible parameters are 'BoxConstraint', 'KernelFunction', 'KernelScale',
'PolynomialOrder', and 'Standardize'. For an
example, see Optimize Classifier Fit Using Bayesian Optimization. Alternatively,
you can use the bayesopt function, as shown in
Optimize Cross-Validated Classifier Using bayesopt. The bayesopt
function allows more flexibility to customize optimization. You can use the
bayesopt function to optimize any parameters, including
parameters that are not eligible to optimize when you use the
fitcsvm function.
You can also try tuning parameters of your classifier manually according to this scheme:
Pass the data to
fitcsvm, and set the name-value pair argument'KernelScale','auto'. Suppose that the trained SVM model is calledSVMModel. The software uses a heuristic procedure to select the kernel scale. The heuristic procedure uses subsampling. Therefore, to reproduce results, set a random number seed usingrngbefore training the classifier.Cross validate the classifier by passing it to
crossval. By default, the software conducts 10-fold cross validation.Pass the cross-validated SVM model to
kfoldLossto estimate and retain the classification error.Retrain the SVM classifier, but adjust the
'KernelScale'and'BoxConstraint'name-value pair arguments.BoxConstraint— One strategy is to try a geometric sequence of the box constraint parameter. For example, take 11 values, from1e-5to1e5by a factor of 10. IncreasingBoxConstraintmight decrease the number of support vectors, but also might increase training time.KernelScale— One strategy is to try a geometric sequence of the RBF sigma parameter scaled at the original kernel scale. Do this by:Retrieving the original kernel scale, e.g.,
ks, using dot notation:ks = SVMModel.KernelParameters.Scale.Use as new kernel scales factors of the original. For example, multiply
ksby the 11 values1e-5to1e5, increasing by a factor of 10.
Choose the model that yields the lowest classification error. You might want to further refine your parameters to obtain better accuracy. Start with your initial parameters and perform another cross-validation step, this time using a factor of 1.2.
Train SVM Classifiers Using Gaussian Kernel
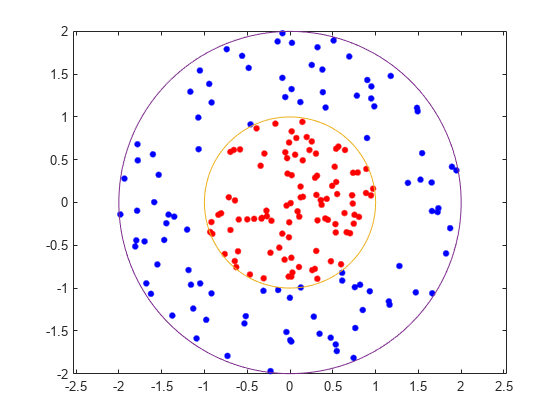
This example shows how to generate a nonlinear classifier with Gaussian kernel function. First, generate one class of points inside the unit disk in two dimensions, and another class of points in the annulus from radius 1 to radius 2. Then, generate a classifier based on the data with the Gaussian radial basis function kernel. The default linear classifier is unsuitable for this problem because the model is circularly symmetric. Set the box constraint parameter to Inf to make a strict classification, meaning no misclassified training points. Other kernel functions might not work with this strict box constraint, since they might be unable to provide a strict classification. Even though the rbf classifier can separate the classes, the result can be overtrained.
Generate 100 points uniformly distributed in the unit disk. To do so, generate a radius r as the square root of a uniform random variable, generate an angle t uniformly in (0, ), and put the point at (r cos(t), r sin(t)).
rng(1); % For reproducibility r = sqrt(rand(100,1)); % Radius t = 2*pi*rand(100,1); % Angle data1 = [r.*cos(t), r.*sin(t)]; % Points
Generate 100 points uniformly distributed in the annulus. The radius is again proportional to a square root, this time a square root of the uniform distribution from 1 through 4.
r2 = sqrt(3*rand(100,1)+1); % Radius t2 = 2*pi*rand(100,1); % Angle data2 = [r2.*cos(t2), r2.*sin(t2)]; % Points
Plot the points, and plot circles of radii 1 and 2 for comparison.
figure plot(data1(:,1),data1(:,2),"r.","MarkerSize",15) hold on plot(data2(:,1),data2(:,2),"b.","MarkerSize",15) fplot(@(t)sin(t),@(t)cos(t)) fplot(@(t)2*sin(t),@(t)2*cos(t)) axis equal hold off
Put the data in one matrix, and make a vector of classifications.
data3 = [data1;data2]; theclass = ones(200,1); theclass(1:100) = -1;
Train an SVM classifier with KernelFunction set to "rbf" and BoxConstraint set to Inf. Plot the decision boundary and flag the support vectors.
% Train the SVM classifier cl = fitcsvm(data3,theclass,"KernelFunction","rbf", ... "BoxConstraint",Inf,"ClassNames",[-1 1]); % Predict scores over the grid d = 0.02; [x1Grid,x2Grid] = meshgrid(min(data3(:,1)):d:max(data3(:,1)), ... min(data3(:,2)):d:max(data3(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(cl,xGrid); % Plot the data and the decision boundary figure h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,"rb","."); hold on fplot(@(t)sin(t),@(t)cos(t)) h(3) = plot(data3(cl.IsSupportVector,1),data3(cl.IsSupportVector,2),"ko"); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],"k") legend(h,["-1","+1","Support Vectors"]) axis equal hold off
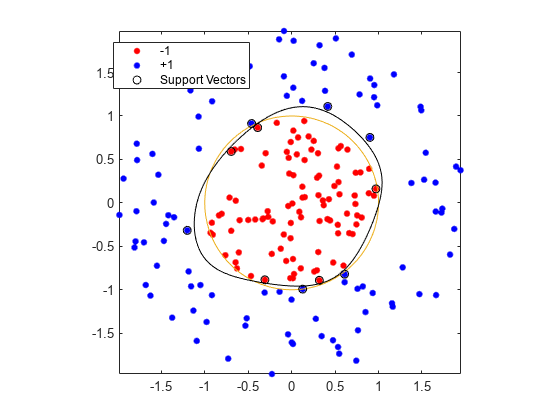
fitcsvm generates a classifier that is close to a circle of radius 1. The difference is due to the random training data.
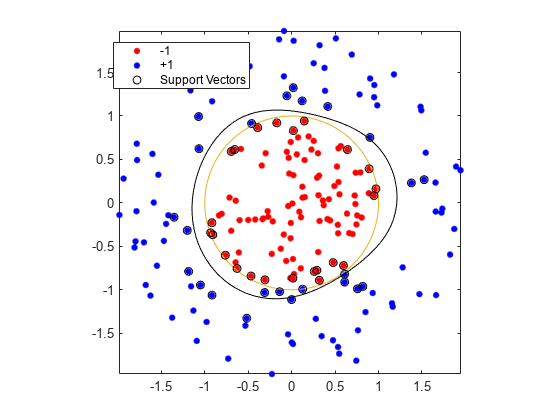
Training with the default parameters makes a more nearly circular classification boundary, but one that misclassifies some training data. Also, the default value of BoxConstraint is 1, and, therefore, there are more support vectors.
cl2 = fitcsvm(data3,theclass,"KernelFunction","rbf"); [~,scores2] = predict(cl2,xGrid); figure h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,"rb","."); hold on fplot(@(t)sin(t),@(t)cos(t)) h(3) = plot(data3(cl2.IsSupportVector,1),data3(cl2.IsSupportVector,2),"ko"); contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],"k") legend(h,["-1","+1","Support Vectors"]) axis equal hold off
Train SVM Classifier Using Custom Kernel
This example shows how to use a custom kernel function, such as the sigmoid kernel, to train SVM classifiers, and adjust custom kernel function parameters.
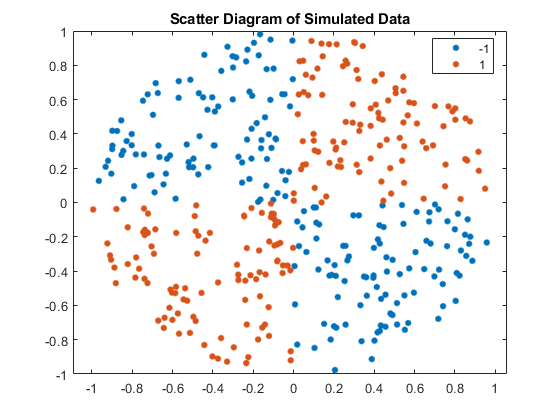
Generate a random set of points within the unit circle. Label points in the first and third quadrants as belonging to the positive class, and those in the second and fourth quadrants in the negative class.
rng(1); % For reproducibility n = 100; % Number of points per quadrant r1 = sqrt(rand(2*n,1)); % Random radii t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3 X1 = [r1.*cos(t1) r1.*sin(t1)]; % Polar-to-Cartesian conversion r2 = sqrt(rand(2*n,1)); t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4 X2 = [r2.*cos(t2) r2.*sin(t2)]; X = [X1; X2]; % Predictors Y = ones(4*n,1); Y(2*n + 1:end) = -1; % Labels
Plot the data.
figure;
gscatter(X(:,1),X(:,2),Y);
title('Scatter Diagram of Simulated Data')
Write a function that accepts two matrices in the feature space as inputs, and transforms them into a Gram matrix using the sigmoid kernel.
function G = mysigmoid(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 1; c = -1; G = tanh(gamma*U*V' + c); end
Save this code as a file named mysigmoid on your MATLAB® path.
Train an SVM classifier using the sigmoid kernel function. It is good practice to standardize the data.
Mdl1 = fitcsvm(X,Y,'KernelFunction','mysigmoid','Standardize',true);
Mdl1 is a ClassificationSVM classifier containing the estimated parameters.
Plot the data, and identify the support vectors and the decision boundary.
% Compute the scores over a grid d = 0.02; % Step size of the grid [x1Grid,x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)),... min(X(:,2)):d:max(X(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; % The grid [~,scores1] = predict(Mdl1,xGrid); % The scores figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl1.IsSupportVector,1),... X(Mdl1.IsSupportVector,2),'ko','MarkerSize',10); % Support vectors contour(x1Grid,x2Grid,reshape(scores1(:,2),size(x1Grid)),[0 0],'k'); % Decision boundary title('Scatter Diagram with the Decision Boundary') legend({'-1','1','Support Vectors'},'Location','Best'); hold off

You can adjust the kernel parameters in an attempt to improve the shape of the decision boundary. This might also decrease the within-sample misclassification rate, but, you should first determine the out-of-sample misclassification rate.
Determine the out-of-sample misclassification rate by using 10-fold cross validation.
CVMdl1 = crossval(Mdl1); misclass1 = kfoldLoss(CVMdl1); misclass1
misclass1 =
0.1350
The out-of-sample misclassification rate is 13.5%.
Write another sigmoid function, but Set gamma = 0.5;.
function G = mysigmoid2(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 0.5; c = -1; G = tanh(gamma*U*V' + c); end
Save this code as a file named mysigmoid2 on your MATLAB® path.
Train another SVM classifier using the adjusted sigmoid kernel. Plot the data and the decision region, and determine the out-of-sample misclassification rate.
Mdl2 = fitcsvm(X,Y,'KernelFunction','mysigmoid2','Standardize',true); [~,scores2] = predict(Mdl2,xGrid); figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl2.IsSupportVector,1),... X(Mdl2.IsSupportVector,2),'ko','MarkerSize',10); title('Scatter Diagram with the Decision Boundary') contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend({'-1','1','Support Vectors'},'Location','Best'); hold off CVMdl2 = crossval(Mdl2); misclass2 = kfoldLoss(CVMdl2); misclass2
misclass2 =
0.0450

After the sigmoid slope adjustment, the new decision boundary seems to provide a better within-sample fit, and the cross-validation rate contracts by more than 66%.
Optimize Classifier Fit Using Bayesian Optimization
This example shows how to optimize an SVM classification using the fitcsvm function and the OptimizeHyperparameters name-value argument.
Generate Data
The classification works on locations of points from a Gaussian mixture model. In The Elements of Statistical Learning, Hastie, Tibshirani, and Friedman (2009), page 17 describes the model. The model begins with generating 10 base points for a "green" class, distributed as 2-D independent normals with mean (1,0) and unit variance. It also generates 10 base points for a "red" class, distributed as 2-D independent normals with mean (0,1) and unit variance. For each class (green and red), generate 100 random points as follows:
Choose a base point m of the appropriate color uniformly at random.
Generate an independent random point with 2-D normal distribution with mean m and variance I/5, where I is the 2-by-2 identity matrix. In this example, use a variance I/50 to show the advantage of optimization more clearly.
Generate the 10 base points for each class.
rng('default') % For reproducibility grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10);
View the base points.
plot(grnpop(:,1),grnpop(:,2),'go') hold on plot(redpop(:,1),redpop(:,2),'ro') hold off
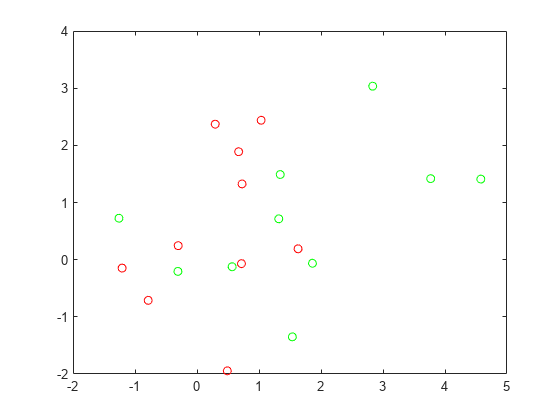
Since some red base points are close to green base points, it can be difficult to classify the data points based on location alone.
Generate the 100 data points of each class.
redpts = zeros(100,2); grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end
View the data points.
figure plot(grnpts(:,1),grnpts(:,2),'go') hold on plot(redpts(:,1),redpts(:,2),'ro') hold off

Prepare Data for Classification
Put the data into one matrix, and make a vector grp that labels the class of each point. 1 indicates the green class, and –1 indicates the red class.
cdata = [grnpts;redpts]; grp = ones(200,1); grp(101:200) = -1;
Prepare Cross-Validation
Set up a partition for cross-validation.
c = cvpartition(200,'KFold',10);This step is optional. If you specify a partition for the optimization, then you can compute an actual cross-validation loss for the returned model.
Optimize Fit
To find a good fit, meaning one with optimal hyperparameters that minimize the cross-validation loss, use Bayesian optimization. Specify a list of hyperparameters to optimize by using the OptimizeHyperparameters name-value argument, and specify optimization options by using the HyperparameterOptimizationOptions name-value argument.
Specify 'OptimizeHyperparameters' as 'auto'. The 'auto' option includes a typical set of hyperparameters to optimize. fitcsvm finds optimal values of BoxConstraint, KernelScale, and Standardize. Set the hyperparameter optimization options to use the cross-validation partition c and to choose the 'expected-improvement-plus' acquisition function for reproducibility. The default acquisition function depends on run time and, therefore, can give varying results.
opts = struct('CVPartition',c,'AcquisitionFunctionName', ... 'expected-improvement-plus'); Mdl = fitcsvm(cdata,grp,'KernelFunction','rbf', ... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',opts)
|====================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Standardize |
| | result | | runtime | (observed) | (estim.) | | | |
|====================================================================================================================|
| 1 | Best | 0.195 | 0.17125 | 0.195 | 0.195 | 193.54 | 0.069073 | false |
| 2 | Accept | 0.345 | 0.068158 | 0.195 | 0.20398 | 43.991 | 277.86 | false |
| 3 | Accept | 0.365 | 0.075044 | 0.195 | 0.20784 | 0.0056595 | 0.042141 | false |
| 4 | Accept | 0.61 | 0.080316 | 0.195 | 0.31714 | 49.333 | 0.0010514 | true |
| 5 | Best | 0.1 | 0.084598 | 0.1 | 0.10005 | 996.27 | 1.3081 | false |
| 6 | Accept | 0.13 | 0.073056 | 0.1 | 0.10003 | 25.398 | 1.7076 | false |
| 7 | Best | 0.085 | 0.078674 | 0.085 | 0.08521 | 930.3 | 0.66262 | false |
| 8 | Accept | 0.35 | 0.068592 | 0.085 | 0.085172 | 0.012972 | 983.4 | true |
| 9 | Best | 0.075 | 0.074766 | 0.075 | 0.077959 | 871.26 | 0.40617 | false |
| 10 | Accept | 0.08 | 0.076745 | 0.075 | 0.077975 | 974.28 | 0.45314 | false |
| 11 | Accept | 0.235 | 0.11206 | 0.075 | 0.077907 | 920.57 | 6.482 | true |
| 12 | Accept | 0.305 | 0.0656 | 0.075 | 0.077922 | 0.0010077 | 1.0212 | true |
| 13 | Best | 0.07 | 0.083098 | 0.07 | 0.073603 | 991.16 | 0.37801 | false |
| 14 | Accept | 0.075 | 0.068284 | 0.07 | 0.073191 | 989.88 | 0.24951 | false |
| 15 | Accept | 0.245 | 0.09127 | 0.07 | 0.073276 | 988.76 | 9.1309 | false |
| 16 | Accept | 0.07 | 0.084731 | 0.07 | 0.071416 | 957.65 | 0.31271 | false |
| 17 | Accept | 0.35 | 0.056762 | 0.07 | 0.071421 | 0.0010579 | 33.692 | true |
| 18 | Accept | 0.085 | 0.069899 | 0.07 | 0.071274 | 48.536 | 0.32107 | false |
| 19 | Accept | 0.07 | 0.079488 | 0.07 | 0.070587 | 742.56 | 0.30798 | false |
| 20 | Accept | 0.61 | 0.073678 | 0.07 | 0.070796 | 865.48 | 0.0010165 | false |
|====================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | Standardize |
| | result | | runtime | (observed) | (estim.) | | | |
|====================================================================================================================|
| 21 | Accept | 0.1 | 0.0701 | 0.07 | 0.070715 | 970.87 | 0.14635 | true |
| 22 | Accept | 0.095 | 0.065318 | 0.07 | 0.07087 | 914.88 | 0.46353 | true |
| 23 | Accept | 0.07 | 0.072814 | 0.07 | 0.070473 | 982.01 | 0.2792 | false |
| 24 | Accept | 0.51 | 0.080293 | 0.07 | 0.070515 | 0.0010005 | 0.014749 | true |
| 25 | Accept | 0.345 | 0.079667 | 0.07 | 0.070533 | 0.0010063 | 972.18 | false |
| 26 | Accept | 0.315 | 0.058903 | 0.07 | 0.07057 | 947.71 | 152.95 | true |
| 27 | Accept | 0.35 | 0.058704 | 0.07 | 0.070605 | 0.0010028 | 43.62 | false |
| 28 | Accept | 0.61 | 0.078135 | 0.07 | 0.070598 | 0.0010405 | 0.0010258 | false |
| 29 | Accept | 0.555 | 0.082626 | 0.07 | 0.070173 | 993.56 | 0.010502 | true |
| 30 | Accept | 0.07 | 0.082082 | 0.07 | 0.070158 | 965.73 | 0.25363 | true |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 12.1728 seconds
Total objective function evaluation time: 2.3647
Best observed feasible point:
BoxConstraint KernelScale Standardize
_____________ ___________ ___________
991.16 0.37801 false
Observed objective function value = 0.07
Estimated objective function value = 0.072292
Function evaluation time = 0.083098
Best estimated feasible point (according to models):
BoxConstraint KernelScale Standardize
_____________ ___________ ___________
957.65 0.31271 false
Estimated objective function value = 0.070158
Estimated function evaluation time = 0.077007

Mdl =
ClassificationSVM
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [-1 1]
ScoreTransform: 'none'
NumObservations: 200
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
Alpha: [66×1 double]
Bias: -0.0910
KernelParameters: [1×1 struct]
BoxConstraints: [200×1 double]
ConvergenceInfo: [1×1 struct]
IsSupportVector: [200×1 logical]
Solver: 'SMO'
Properties, Methods
fitcsvm returns a ClassificationSVM model object that uses the best estimated feasible point. The best estimated feasible point is the set of hyperparameters that minimizes the upper confidence bound of the cross-validation loss based on the underlying Gaussian process model of the Bayesian optimization process.
The Bayesian optimization process internally maintains a Gaussian process model of the objective function. The objective function is the cross-validated misclassification rate for classification. For each iteration, the optimization process updates the Gaussian process model and uses the model to find a new set of hyperparameters. Each line of the iterative display shows the new set of hyperparameters and these column values:
Objective— Objective function value computed at the new set of hyperparameters.Objective runtime— Objective function evaluation time.Eval result— Result report, specified asAccept,Best, orError.Acceptindicates that the objective function returns a finite value, andErrorindicates that the objective function returns a value that is not a finite real scalar.Bestindicates that the objective function returns a finite value that is lower than previously computed objective function values.BestSoFar(observed)— The minimum objective function value computed so far. This value is either the objective function value of the current iteration (if theEval resultvalue for the current iteration isBest) or the value of the previousBestiteration.BestSoFar(estim.)— At each iteration, the software estimates the upper confidence bounds of the objective function values, using the updated Gaussian process model, at all the sets of hyperparameters tried so far. Then the software chooses the point with the minimum upper confidence bound. TheBestSoFar(estim.)value is the objective function value returned by thepredictObjectivefunction at the minimum point.
The plot below the iterative display shows the BestSoFar(observed) and BestSoFar(estim.) values in blue and green, respectively.
The returned object Mdl uses the best estimated feasible point, that is, the set of hyperparameters that produces the BestSoFar(estim.) value in the final iteration based on the final Gaussian process model.
You can obtain the best point from the HyperparameterOptimizationResults property or by using the bestPoint function.
Mdl.HyperparameterOptimizationResults.XAtMinEstimatedObjective
ans=1×3 table
BoxConstraint KernelScale Standardize
_____________ ___________ ___________
957.65 0.31271 false
[x,CriterionValue,iteration] = bestPoint(Mdl.HyperparameterOptimizationResults)
x=1×3 table
BoxConstraint KernelScale Standardize
_____________ ___________ ___________
957.65 0.31271 false
CriterionValue = 0.0724
iteration = 16
By default, the bestPoint function uses the 'min-visited-upper-confidence-interval' criterion. This criterion chooses the hyperparameters obtained from the 16th iteration as the best point. CriterionValue is the upper bound of the cross-validated loss computed by the final Gaussian process model. Compute the actual cross-validated loss by using the partition c.
L_MinEstimated = kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c, ... 'KernelFunction','rbf','BoxConstraint',x.BoxConstraint, ... 'KernelScale',x.KernelScale,'Standardize',x.Standardize=='true'))
L_MinEstimated = 0.0700
The actual cross-validated loss is close to the estimated value. The Estimated objective function value is displayed below the plot of the optimization results.
You can also extract the best observed feasible point (that is, the last Best point in the iterative display) from the HyperparameterOptimizationResults property or by specifying Criterion as 'min-observed'.
Mdl.HyperparameterOptimizationResults.XAtMinObjective
ans=1×3 table
BoxConstraint KernelScale Standardize
_____________ ___________ ___________
991.16 0.37801 false
[x_observed,CriterionValue_observed,iteration_observed] = ... bestPoint(Mdl.HyperparameterOptimizationResults,'Criterion','min-observed')
x_observed=1×3 table
BoxConstraint KernelScale Standardize
_____________ ___________ ___________
991.16 0.37801 false
CriterionValue_observed = 0.0700
iteration_observed = 13
The 'min-observed' criterion chooses the hyperparameters obtained from the 13th iteration as the best point. CriterionValue_observed is the actual cross-validated loss computed using the selected hyperparameters. For more information, see the Criterion name-value argument of bestPoint.
Visualize the optimized classifier.
d = 0.02; [x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)), ... min(cdata(:,2)):d:max(cdata(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(Mdl,xGrid); figure h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*'); hold on h(3) = plot(cdata(Mdl.IsSupportVector,1), ... cdata(Mdl.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'},'Location','Southeast');

Evaluate Accuracy on New Data
Generate and classify new test data points.
grnobj = gmdistribution(grnpop,.2*eye(2)); redobj = gmdistribution(redpop,.2*eye(2)); newData = random(grnobj,10); newData = [newData;random(redobj,10)]; grpData = ones(20,1); % green = 1 grpData(11:20) = -1; % red = -1 v = predict(Mdl,newData);
Compute the misclassification rates on the test data set.
L_Test = loss(Mdl,newData,grpData)
L_Test = 0.2000
Determine which new data points are classified correctly. Format the correctly classified points in red squares and the incorrectly classified points in black squares.
h(4:5) = gscatter(newData(:,1),newData(:,2),v,'mc','**'); mydiff = (v == grpData); % Classified correctly for ii = mydiff % Plot red squares around correct pts h(6) = plot(newData(ii,1),newData(ii,2),'rs','MarkerSize',12); end for ii = not(mydiff) % Plot black squares around incorrect pts h(7) = plot(newData(ii,1),newData(ii,2),'ks','MarkerSize',12); end legend(h,{'-1 (training)','+1 (training)','Support Vectors', ... '-1 (classified)','+1 (classified)', ... 'Correctly Classified','Misclassified'}, ... 'Location','Southeast'); hold off

Plot Posterior Probability Regions for SVM Classification Models
This example shows how to predict posterior probabilities of SVM models over a grid of observations, and then plot the posterior probabilities over the grid. Plotting posterior probabilities exposes decision boundaries.
Load Fisher's iris data set. Train the classifier using the petal lengths and widths, and remove the virginica species from the data.
load fisheriris classKeep = ~strcmp(species,'virginica'); X = meas(classKeep,3:4); y = species(classKeep);
Train an SVM classifier using the data. It is good practice to specify the order of the classes.
SVMModel = fitcsvm(X,y,'ClassNames',{'setosa','versicolor'});
Estimate the optimal score transformation function.
rng(1); % For reproducibility
[SVMModel,ScoreParameters] = fitPosterior(SVMModel); Warning: Classes are perfectly separated. The optimal score-to-posterior transformation is a step function.
ScoreParameters
ScoreParameters = struct with fields:
Type: 'step'
LowerBound: -0.8431
UpperBound: 0.6897
PositiveClassProbability: 0.5000
The optimal score transformation function is the step function because the classes are separable. The fields LowerBound and UpperBound of ScoreParameters indicate the lower and upper end points of the interval of scores corresponding to observations within the class-separating hyperplanes (the margin). No training observation falls within the margin. If a new score is in the interval, then the software assigns the corresponding observation a positive class posterior probability, i.e., the value in the PositiveClassProbability field of ScoreParameters.
Define a grid of values in the observed predictor space. Predict the posterior probabilities for each instance in the grid.
xMax = max(X); xMin = min(X); d = 0.01; [x1Grid,x2Grid] = meshgrid(xMin(1):d:xMax(1),xMin(2):d:xMax(2)); [~,PosteriorRegion] = predict(SVMModel,[x1Grid(:),x2Grid(:)]);
Plot the positive class posterior probability region and the training data.
figure; contourf(x1Grid,x2Grid,... reshape(PosteriorRegion(:,2),size(x1Grid,1),size(x1Grid,2))); h = colorbar; h.Label.String = 'P({\it{versicolor}})'; h.YLabel.FontSize = 16; colormap jet; hold on gscatter(X(:,1),X(:,2),y,'mc','.x',[15,10]); sv = X(SVMModel.IsSupportVector,:); plot(sv(:,1),sv(:,2),'yo','MarkerSize',15,'LineWidth',2); axis tight hold off
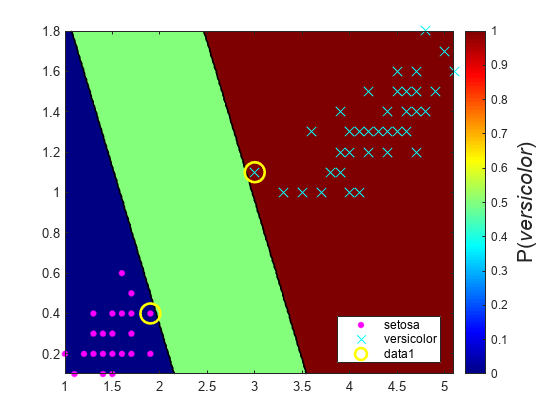
In two-class learning, if the classes are separable, then there are three regions: one where observations have positive class posterior probability 0, one where it is 1, and the other where it is the positive class prior probability.
Analyze Images Using Linear Support Vector Machines
This example shows how to determine which quadrant of an image a shape occupies by training an error-correcting output codes (ECOC) model comprised of linear SVM binary learners. This example also illustrates the disk-space consumption of ECOC models that store support vectors, their labels, and the estimated coefficients.
Create the Data Set
Randomly place a circle with radius five in a 50-by-50 image. Make 5000 images. Create a label for each image indicating the quadrant that the circle occupies. Quadrant 1 is in the upper right, quadrant 2 is in the upper left, quadrant 3 is in the lower left, and quadrant 4 is in the lower right. The predictors are the intensities of each pixel.
d = 50; % Height and width of the images in pixels n = 5e4; % Sample size X = zeros(n,d^2); % Predictor matrix preallocation Y = zeros(n,1); % Label preallocation theta = 0:(1/d):(2*pi); r = 5; % Circle radius rng(1); % For reproducibility for j = 1:n figmat = zeros(d); % Empty image c = datasample((r + 1):(d - r - 1),2); % Random circle center x = r*cos(theta) + c(1); % Make the circle y = r*sin(theta) + c(2); idx = sub2ind([d d],round(y),round(x)); % Convert to linear indexing figmat(idx) = 1; % Draw the circle X(j,:) = figmat(:); % Store the data Y(j) = (c(2) >= floor(d/2)) + 2*(c(2) < floor(d/2)) + ... (c(1) < floor(d/2)) + ... 2*((c(1) >= floor(d/2)) & (c(2) < floor(d/2))); % Determine the quadrant end
Plot an observation.
figure imagesc(figmat) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant %d',Y(end)))

Train the ECOC Model
Use a 25% holdout sample and specify the training and holdout sample indices.
p = 0.25; CVP = cvpartition(Y,'Holdout',p); % Cross-validation data partition isIdx = training(CVP); % Training sample indices oosIdx = test(CVP); % Test sample indices
Create an SVM template that specifies storing the support vectors of the binary learners. Pass it and the training data to fitcecoc to train the model. Determine the training sample classification error.
t = templateSVM('SaveSupportVectors',true); MdlSV = fitcecoc(X(isIdx,:),Y(isIdx),'Learners',t); isLoss = resubLoss(MdlSV)
isLoss = 0
MdlSV is a trained ClassificationECOC multiclass model. It stores the training data and the support vectors of each binary learner. For large data sets, such as those in image analysis, the model can consume a lot of memory.
Determine the amount of disk space that the ECOC model consumes.
infoMdlSV = whos('MdlSV');
mbMdlSV = infoMdlSV.bytes/1.049e6mbMdlSV = 763.6127
The model consumes 763.6 MB.
Improve Model Efficiency
You can assess out-of-sample performance. You can also assess whether the model has been overfit with a compacted model that does not contain the support vectors, their related parameters, and the training data.
Discard the support vectors and related parameters from the trained ECOC model. Then, discard the training data from the resulting model by using compact.
Mdl = discardSupportVectors(MdlSV); CMdl = compact(Mdl); info = whos('Mdl','CMdl'); [bytesCMdl,bytesMdl] = info.bytes; memReduction = 1 - [bytesMdl bytesCMdl]/infoMdlSV.bytes
memReduction = 1×2
0.0626 0.9996
In this case, discarding the support vectors reduces the memory consumption by about 6%. Compacting and discarding support vectors reduces the size by about 99.96%.
An alternative way to manage support vectors is to reduce their numbers during training by specifying a larger box constraint, such as 100. Though SVM models that use fewer support vectors are more desirable and consume less memory, increasing the value of the box constraint tends to increase the training time.
Remove MdlSV and Mdl from the workspace.
clear Mdl MdlSV
Assess Holdout Sample Performance
Calculate the classification error of the holdout sample. Plot a sample of the holdout sample predictions.
oosLoss = loss(CMdl,X(oosIdx,:),Y(oosIdx))
oosLoss = 0
yHat = predict(CMdl,X(oosIdx,:)); nVec = 1:size(X,1); oosIdx = nVec(oosIdx); figure; for j = 1:9 subplot(3,3,j) imagesc(reshape(X(oosIdx(j),:),[d d])) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant: %d',yHat(j))) end text(-1.33*d,4.5*d + 1,'Predictions','FontSize',17)

The model does not misclassify any holdout sample observations.
See Also
fitcsvm | bayesopt | kfoldLoss
Topics
References
[1] Hastie, T., R. Tibshirani, and J. Friedman. The Elements of Statistical Learning, second edition. New York: Springer, 2008.
[2] Christianini, N., and J. Shawe-Taylor. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge, UK: Cambridge University Press, 2000.
[3] Fan, R.-E., P.-H. Chen, and C.-J. Lin. “Working set selection using second order information for training support vector machines.” Journal of Machine Learning Research, Vol 6, 2005, pp. 1889–1918.
[4] Kecman V., T. -M. Huang, and M. Vogt. “Iterative Single Data Algorithm for Training Kernel Machines from Huge Data Sets: Theory and Performance.” In Support Vector Machines: Theory and Applications. Edited by Lipo Wang, 255–274. Berlin: Springer-Verlag, 2005.