Optimize Cross-Validated Classifier Using bayesopt
This example shows how to optimize an SVM classification using the bayesopt function.
Alternatively, you can optimize a classifier by using the OptimizeHyperparameters name-value argument. For an example, see Optimize Classifier Fit Using Bayesian Optimization.
Generate Data
The classification works on locations of points from a Gaussian mixture model. In The Elements of Statistical Learning, Hastie, Tibshirani, and Friedman (2009), page 17 describes the model. The model begins with generating 10 base points for a "green" class, distributed as 2-D independent normals with mean (1,0) and unit variance. It also generates 10 base points for a "red" class, distributed as 2-D independent normals with mean (0,1) and unit variance. For each class (green and red), generate 100 random points as follows:
Choose a base point m of the appropriate color uniformly at random.
Generate an independent random point with 2-D normal distribution with mean m and variance I/5, where I is the 2-by-2 identity matrix. In this example, use a variance I/50 to show the advantage of optimization more clearly.
Generate the 10 base points for each class.
rng('default') % For reproducibility grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10);
View the base points.
plot(grnpop(:,1),grnpop(:,2),'go') hold on plot(redpop(:,1),redpop(:,2),'ro') hold off
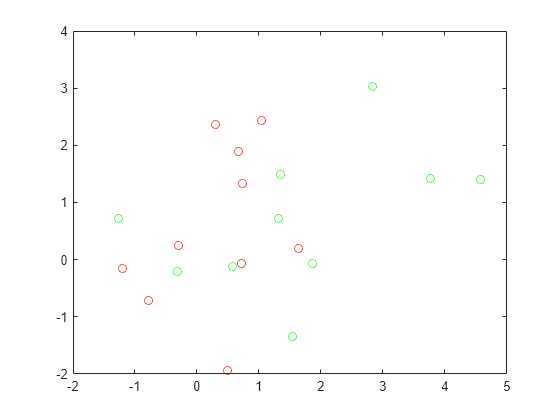
Since some red base points are close to green base points, it can be difficult to classify the data points based on location alone.
Generate the 100 data points of each class.
redpts = zeros(100,2);grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end
View the data points.
figure plot(grnpts(:,1),grnpts(:,2),'go') hold on plot(redpts(:,1),redpts(:,2),'ro') hold off
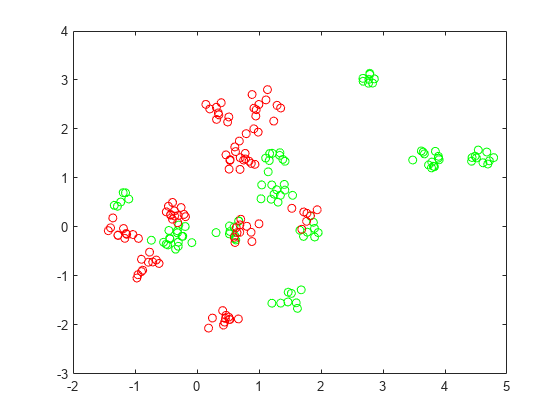
Prepare Data for Classification
Put the data into one matrix, and make a vector grp that labels the class of each point. 1 indicates the green class, and -1 indicates the red class.
cdata = [grnpts;redpts]; grp = ones(200,1); grp(101:200) = -1;
Prepare Cross-Validation
Set up a partition for cross-validation. This step fixes the train and test sets that the optimization uses at each step.
c = cvpartition(200,'KFold',10);Prepare Variables for Bayesian Optimization
Set up a function that takes an input z = [rbf_sigma,boxconstraint] and returns the cross-validation loss value of z. Take the components of z as positive, log-transformed variables between 1e-5 and 1e5. Choose a wide range, because you don't know which values are likely to be good.
sigma = optimizableVariable('sigma',[1e-5,1e5],'Transform','log'); box = optimizableVariable('box',[1e-5,1e5],'Transform','log');
Objective Function
This function handle computes the cross-validation loss at parameters [sigma,box]. For details, see kfoldLoss.
bayesopt passes the variable z to the objective function as a one-row table.
minfn = @(z)kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,... 'KernelFunction','rbf','BoxConstraint',z.box,... 'KernelScale',z.sigma));
Optimize Classifier
Search for the best parameters [sigma,box] using bayesopt. For reproducibility, choose the 'expected-improvement-plus' acquisition function. The default acquisition function depends on run time, and so can give varying results.
results = bayesopt(minfn,[sigma,box],'IsObjectiveDeterministic',true,... 'AcquisitionFunctionName','expected-improvement-plus')
|=====================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | sigma | box |
| | result | | runtime | (observed) | (estim.) | | |
|=====================================================================================================|
| 1 | Best | 0.61 | 0.44749 | 0.61 | 0.61 | 0.00013375 | 13929 |
| 2 | Best | 0.345 | 0.42546 | 0.345 | 0.345 | 24526 | 1.936 |
| 3 | Accept | 0.61 | 0.30024 | 0.345 | 0.345 | 0.0026459 | 0.00084929 |
| 4 | Accept | 0.345 | 0.33654 | 0.345 | 0.345 | 3506.3 | 6.7427e-05 |
| 5 | Accept | 0.345 | 0.15382 | 0.345 | 0.345 | 9135.2 | 571.87 |
| 6 | Accept | 0.345 | 0.11334 | 0.345 | 0.345 | 99701 | 10223 |
| 7 | Best | 0.295 | 0.1098 | 0.295 | 0.295 | 455.88 | 9957.4 |
| 8 | Best | 0.24 | 1.4009 | 0.24 | 0.24 | 31.56 | 99389 |
| 9 | Accept | 0.24 | 1.7838 | 0.24 | 0.24 | 10.451 | 64429 |
| 10 | Accept | 0.35 | 0.10767 | 0.24 | 0.24 | 17.331 | 1.0264e-05 |
| 11 | Best | 0.23 | 1.0555 | 0.23 | 0.23 | 16.005 | 90155 |
| 12 | Best | 0.1 | 0.1715 | 0.1 | 0.1 | 0.36562 | 80878 |
| 13 | Accept | 0.115 | 0.11514 | 0.1 | 0.1 | 0.1793 | 68459 |
| 14 | Accept | 0.105 | 0.14588 | 0.1 | 0.1 | 0.2267 | 95421 |
| 15 | Best | 0.095 | 0.1027 | 0.095 | 0.095 | 0.28999 | 0.0058227 |
| 16 | Best | 0.075 | 0.11732 | 0.075 | 0.075 | 0.30554 | 8.9017 |
| 17 | Accept | 0.085 | 0.10669 | 0.075 | 0.075 | 0.41122 | 4.4476 |
| 18 | Accept | 0.085 | 0.098685 | 0.075 | 0.075 | 0.25565 | 7.8038 |
| 19 | Accept | 0.075 | 0.12188 | 0.075 | 0.075 | 0.32869 | 18.076 |
| 20 | Accept | 0.085 | 0.11217 | 0.075 | 0.075 | 0.32442 | 5.2118 |
|=====================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | sigma | box |
| | result | | runtime | (observed) | (estim.) | | |
|=====================================================================================================|
| 21 | Accept | 0.3 | 0.13662 | 0.075 | 0.075 | 1.3592 | 0.0098067 |
| 22 | Accept | 0.12 | 0.10405 | 0.075 | 0.075 | 0.17515 | 0.00070913 |
| 23 | Accept | 0.175 | 0.12327 | 0.075 | 0.075 | 0.1252 | 0.010749 |
| 24 | Accept | 0.105 | 0.10465 | 0.075 | 0.075 | 1.1664 | 31.13 |
| 25 | Accept | 0.1 | 0.12135 | 0.075 | 0.075 | 0.57465 | 2013.8 |
| 26 | Accept | 0.12 | 0.12251 | 0.075 | 0.075 | 0.42922 | 1.1602e-05 |
| 27 | Accept | 0.12 | 0.11118 | 0.075 | 0.075 | 0.42956 | 0.00027218 |
| 28 | Accept | 0.095 | 0.098285 | 0.075 | 0.075 | 0.4806 | 13.452 |
| 29 | Accept | 0.105 | 0.12514 | 0.075 | 0.075 | 0.19755 | 943.87 |
| 30 | Accept | 0.205 | 0.1268 | 0.075 | 0.075 | 3.5051 | 93.492 |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 47.7286 seconds
Total objective function evaluation time: 8.5004
Best observed feasible point:
sigma box
_______ ______
0.30554 8.9017
Observed objective function value = 0.075
Estimated objective function value = 0.075
Function evaluation time = 0.11732
Best estimated feasible point (according to models):
sigma box
_______ ______
0.32869 18.076
Estimated objective function value = 0.075
Estimated function evaluation time = 0.10997


results =
BayesianOptimization with properties:
ObjectiveFcn: @(z)kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,'KernelFunction','rbf','BoxConstraint',z.box,'KernelScale',z.sigma))
VariableDescriptions: [1×2 optimizableVariable]
Options: [1×1 struct]
MinObjective: 0.0750
XAtMinObjective: [1×2 table]
MinEstimatedObjective: 0.0750
XAtMinEstimatedObjective: [1×2 table]
NumObjectiveEvaluations: 30
TotalElapsedTime: 47.7286
NextPoint: [1×2 table]
XTrace: [30×2 table]
ObjectiveTrace: [30×1 double]
ConstraintsTrace: []
UserDataTrace: {30×1 cell}
ObjectiveEvaluationTimeTrace: [30×1 double]
IterationTimeTrace: [30×1 double]
ErrorTrace: [30×1 double]
FeasibilityTrace: [30×1 logical]
FeasibilityProbabilityTrace: [30×1 double]
IndexOfMinimumTrace: [30×1 double]
ObjectiveMinimumTrace: [30×1 double]
EstimatedObjectiveMinimumTrace: [30×1 double]
Obtain the best estimated feasible point from the XAtMinEstimatedObjective property or by using the bestPoint function. By default, the bestPoint function uses the 'min-visited-upper-confidence-interval' criterion. For details, see the Criterion name-value argument of bestPoint.
results.XAtMinEstimatedObjective
ans=1×2 table
sigma box
_______ ______
0.32869 18.076
z = bestPoint(results)
z=1×2 table
sigma box
_______ ______
0.32869 18.076
Use the best point to train a new, optimized SVM classifier.
SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf', ... 'KernelScale',z.sigma,'BoxConstraint',z.box);
To visualize the support vector classifier, predict scores over a grid.
d = 0.02;
[x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)), ...
min(cdata(:,2)):d:max(cdata(:,2)));
xGrid = [x1Grid(:),x2Grid(:)];
[~,scores] = predict(SVMModel,xGrid);Plot the classification boundaries.
figure h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*'); hold on h(3) = plot(cdata(SVMModel.IsSupportVector,1) ,... cdata(SVMModel.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'},'Location','Southeast');

Evaluate Accuracy on New Data
Generate and classify new test data points.
grnobj = gmdistribution(grnpop,.2*eye(2)); redobj = gmdistribution(redpop,.2*eye(2)); newData = random(grnobj,10); newData = [newData;random(redobj,10)]; grpData = ones(20,1); % green = 1 grpData(11:20) = -1; % red = -1 v = predict(SVMModel,newData);
Compute the misclassification rates on the test data set.
L = loss(SVMModel,newData,grpData)
L = 0.3500
See which new data points are correctly classified. Circle the correctly classified points in red, and the incorrectly classified points in black.
h(4:5) = gscatter(newData(:,1),newData(:,2),v,'mc','**'); mydiff = (v == grpData); % Classified correctly for ii = mydiff % Plot red squares around correct pts h(6) = plot(newData(ii,1),newData(ii,2),'rs','MarkerSize',12); end for ii = not(mydiff) % Plot black squares around incorrect pts h(7) = plot(newData(ii,1),newData(ii,2),'ks','MarkerSize',12); end legend(h,{'-1 (training)','+1 (training)','Support Vectors', ... '-1 (classified)','+1 (classified)', ... 'Correctly Classified','Misclassified'}, ... 'Location','Southeast'); hold off

See Also
bayesopt | optimizableVariable