Spectrum Analyzer
Display frequency spectrum
Libraries:
DSP System Toolbox /
Sinks
Audio Toolbox /
Sinks
DSP System Toolbox HDL Support /
Sinks
Description
The Spectrum Analyzer block, referred to here as the scope, displays frequency-domain signals and the frequency spectrum of time-domain signals. The scope shows the spectrum view and the spectrogram view. The block algorithm performs spectral estimation using the filter bank method and Welch's method of averaged modified periodograms. You can customize the spectrum analyzer display to show the data and the measurement information that you need. For more details, see Algorithms.
You can use the Spectrum Analyzer block in models running in
Normal or Accelerator
simulation modes. You can also use the Spectrum Analyzer block in models
running in Rapid Accelerator or
External simulation modes with some limitations.
You can use the Spectrum Analyzer block inside all subsystems and conditional subsystems. Conditional subsystems include enabled subsystems, triggered subsystems, enabled and triggered subsystems, and function-call subsystems. See Conditionally Executed Subsystems Overview (Simulink) for more information.
Measurements
Cursor Measurements — Measure signal values using vertical and horizontal cursors.
Peak Finder Measurements — Find maxima and show the x-axis values at which they occur.
Channel Measurements — Measure the occupied bandwidth or adjacent channel power ratio (ACPR).
Distortion Measurements — Measure harmonic distortion and intermodulation distortion.
Spectral Mask — Visualize spectrum limits and compare spectrum values to specification values.
Programmatic Control
Configure and display the spectrum analyzer settings from the command line with
the SpectrumAnalyzerBlockConfiguration
object.
Examples
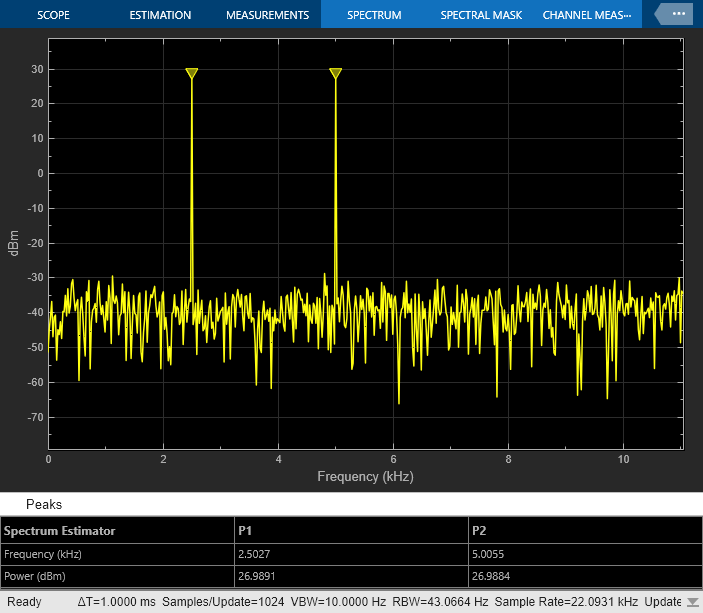
This example shows how to visualize frequency input signals with the Spectrum Analyzer block.

To visualize frequency-domain input signals using a Spectrum Analyzer block, in the Estimation tab of the Spectrum Analyzer toolstrip, set Input Domain to Frequency. In the Spectrum tab, clear the Two-Sided Spectrum parameter.
Run the model. You can see two peaks. To measure the peaks, enable Peak Finder in the Measurements tab.
Decimate a sinusoidal signal by varying the decimation factor using the Variable FIR Decimation block. You can vary the decimation factor in the block dialog box or through an input port while the simulation is running.
Open and Inspect Model
Open the DisplayVariableSizeSignalonSpectrumAnalyzer model.
The input signal in the model is a sum of two sine waves with the frequencies of 1 kHz and 10 kHz, sample time of 1/44100 s, and contains 256 samples per frame. The Random Source block adds zero-mean white Gaussian noise with a variance of 0.05 to the sum of sine waves.
Pass this signal through the Variable FIR Decimation block. The Maximum decimation factor parameter in the block is set to 24. You can specify the decimation factor through the input port and vary it using the Manual Switch block. The output of the Variable FIR Decimation block is a variable-size signal whose frame size varies according to the decimation factor that you specify.
Run Model
Visualize the spectrum of the decimated signal in the spectrum analyzer. The sample rate of the spectrum analyzer updates based on the frame size of the signal and the sample rate of the signal.
When you set the decimation factor to 2, the output frame size is half the input frame size, and the spectrum analyzer uses a sample rate of 44100/2 or 22.05 kHz.

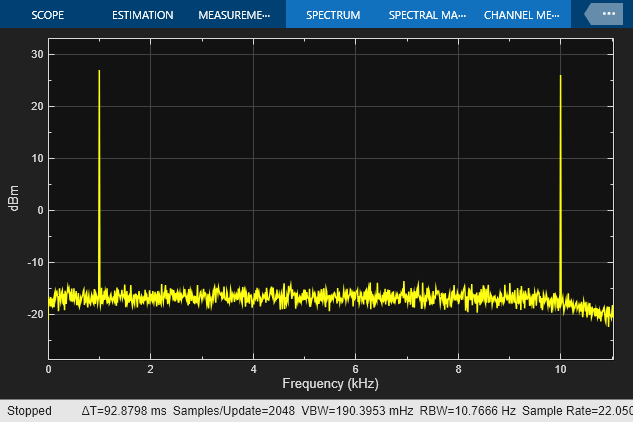
While the simulation is running, change the decimation factor to 4. You can see that the sample rate of the spectrum analyzer adjusts to 44100/4 or 11.025 kHz. The tone at 1 kHz remains the same while the tone at 10 kHz is no longer visible in the spectrum analyzer since the span of the spectrum is now [0 Fs/2] = [0 5.5125 kHz].


Compute and display the power spectrum of a noisy sinusoidal input signal using the Spectrum Analyzer block. Measure the cursor placements, adjacent channel power ratio, distortion, and peak values in the spectrum by enabling these block configuration properties:
CursorMeasurementsChannelMeasurementsDistortionMeasurementsPeakFinder
Open and Inspect the Model
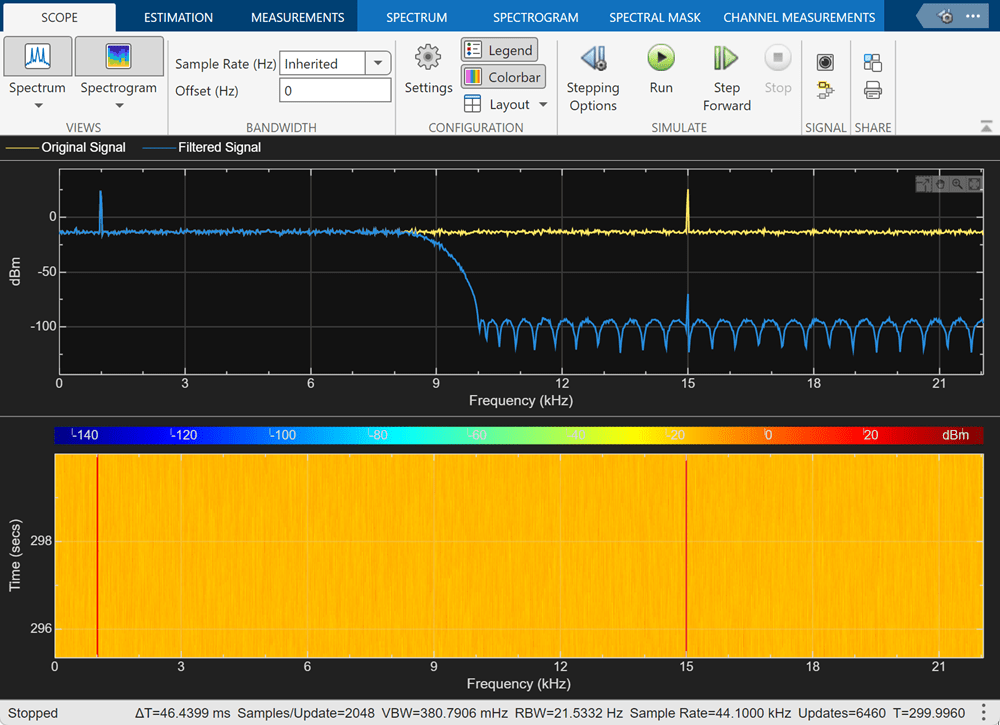
Filter a streaming noisy sinusoidal input signal using a Lowpass Filter block. The input signal consists of two sinusoidal tones: 1 kHz and 15 kHz. The noise is white Gaussian noise with a mean of 0 and a variance of 0.05. The sampling frequency is 44.1 kHz. Open the model and inspect the parameter values in the blocks.
model = 'spectrumanalyzer_measurements.slx';
open_system(model)
Access the configuration properties of the Spectrum Analyzer block using the get_param function.
sablock = 'spectrumanalyzer_measurements/Spectrum Analyzer'; cfg = get_param(sablock,'ScopeConfiguration');
Enable Measurements Data
To obtain the measurements, set the Enabled property to true. Label the peak measurements.
cfg.CursorMeasurements.Enabled = true; cfg.ChannelMeasurements.Enabled = true; cfg.DistortionMeasurements.Enabled = true; cfg.PeakFinder.Enabled = true; cfg.PeakFinder.LabelPeaks = true;
Simulate the Model
Run the model. The Spectrum Analyzer block compares the original spectrum with the filtered spectrum.
sim(model)
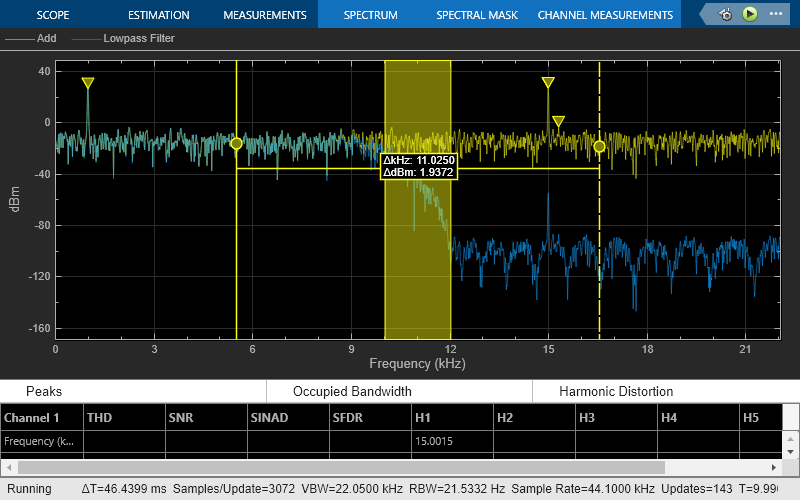
The panels at the bottom of the spectrum analyzer window display the measurements that you have enabled.
Use getMeasurementsData function
Use the getMeasurementsData function to obtain the measurements programmatically.
data = getMeasurementsData(cfg)
data =
1×5 table
SimulationTime PeakFinder CursorMeasurements ChannelMeasurements DistortionMeasurements
______________ __________ __________________ ___________________ ______________________
{[99.9967]} 1×1 struct 1×1 struct 1×1 struct 1×1 struct
The values shown in the measurement panels match the values shown in data. You can access the individual fields of data to obtain the various measurements programmatically.
Compare Peak Values
As an example, compare the peak values. Verify that the peak values obtained by data.PeakFinder match with the values in the spectrum analyzer window.
peakvalues = data.PeakFinder.Value frequencieskHz = data.PeakFinder.Frequency/1000
peakvalues =
26.8789
26.3475
-3.2674
frequencieskHz =
15.0015
1.0049
21.2174
Extended Examples
Spectrum Analyzer Measurements
Use the Spectrum Analyzer block for harmonic distortion measurements (such as THD, SNR, SINAD, and SFDR), third-order intermodulation (TOI) distortion measurements, and adjacent channel power ratio (ACPR) measurements. The example also shows you how to view time-varying spectra by using a spectrogram and automatic peak detection. The example includes five amplifier models, with each model representing a typical setup to perform one of the measurements.
High Resolution Spectral Analysis in Simulink
Perform spectral estimation in Simulink® using the filter bank method, and compare the performance with the Welch's averaged modified periodogram method.
Ports
Input
Connect the signals you want to visualize. You can have up to 96 input ports. Input signals must have these characteristics:
Signal Domain — Frequency or time signals.
Type — Discrete signals.
Data type — Any data type that Simulink supports. See Data Types Supported by Simulink (Simulink).
Dimension — One dimensional (vector), two dimensional (matrix), or multidimensional (array) signals. Input signal must have a fixed number of channels. See Signal Dimensions (Simulink) and Determine Signal Dimensions (Simulink).
The Spectrum Analyzer block supports variable-size input signals, that is, the frame size of the signals can change during simulation. When the signal frame size changes, the sample rate the scope uses changes accordingly, which in turn updates the frequency span of the spectrum display. For an example that shows this behavior, see Display Variable-Size Input Signals on Spectrum Analyzer.
The Spectrum Analyzer block accepts fixed-point input, but
converts it to double for display.
This port is unnamed until you enable one of these inputs ports:
F
RBW
VBW
(since R2024a)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Complex Number Support: Yes
Specify the frequencies in Hz. The frequency vector must be a finite, monotonically increasing, column vector with two or more elements. The number of frequency vector points must be equal to the input frame size. You can also specify the frequencies using the Frequency (Hz) parameter on the Estimation tab.
Dependency
To enable this port, set the:
Input Domain parameter on the Estimation tab to
Frequency.Frequency (Hz) parameter on the Estimation tab to
Input port.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point
Specify the resolution bandwidth in Hz through this port. RBW defines the smallest positive frequency that can be resolved by the scope. You can also specify the RBW value using the RBW (Hz) parameter on the Estimation tab.
Dependency
To enable this port, set the RBW (Hz) parameter
on the Estimation tab to Input
port.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point
Specify the video bandwidth in Hz through this port. Video bandwidth is the bandwidth of the lowpass filter that the scope uses to average or smooth the noise in the signal before displaying it. You can also specify the VBW value using the VBW (Hz) parameter on the Estimation tab.
Dependency
To enable this port, set the:
Input Domain parameter on the Estimation tab to
Time.Averaging Method parameter on the Estimation tab to
VBW.VBW (Hz) parameter on the Estimation tab to
Input port.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point
Parameters
Scope Tab
Views
Set the type of spectrum to display as one of these values:
Power— Spectrum Analyzer shows the power spectrum.Power Density— Spectrum Analyzer shows the power spectral density. The power spectral density is the squared magnitude of the spectrum normalized to a bandwidth of 1 Hz.RMS— Spectrum Analyzer shows the root mean squared spectrum. Use this option to view the frequency of voltage or current signals.
Tunable: Yes
Dependency
To enable this parameter, set the Input
Domain parameter on the
Estimation tab to
Time.
Programmatic Use
Block Parameter:
SpectrumType |
| Type: character vector or string scalar |
Set the type of spectrogram to display as one of these values:
Power— Spectrum Analyzer shows the power spectrogram.Power Density— Spectrum Analyzer shows the power density of the spectrogram. The power spectrogram density is the squared magnitude of the spectrogram normalized to a bandwidth of 1 Hz.RMS— Spectrum Analyzer shows the root mean square of the spectrogram. The root-mean-square shows the square root of the mean square. Use this option to view the frequency of voltage or current signals.
Tunable: Yes
Dependency
To enable this parameter, set the Input
Domain parameter on the
Estimation tab to
Time.
Programmatic Use
Block Parameter:
SpectrumType |
| Type: character vector or string scalar |
Bandwidth
Specify the sample rate the scope uses in Hz as one of the following:
Inherited— Use this option to specify the same sample rate as the input signal.Positive scalar — The sample rate you specify must be at least twice the sample rate of the input signal. Otherwise, you might see unexpected behavior when visualizing your signal in the scope due to aliasing.
When the signal frame size changes, the sample rate the scope uses changes accordingly, which in turn updates the frequency span of the spectrum display. For an example that shows this behavior, see Display Variable-Size Input Signals on Spectrum Analyzer.
To display the sample rate on the status bar, click the
icon in the status bar and select Sample Rate.
Programmatic Use
Block Parameter:
SampleRate, SampleRateSource |
Type:
double |
Tunable: Yes
Specify the offset to apply to the frequency axis (x-axis) in units of Hz as one of the following:
Scalar — Apply the same frequency offset to all channels.
Vector — Apply a specific frequency offset for each channel. The vector length must be equal to the number of input channels.
The overall span must fall within the Nyquist Frequency Interval. You can control the overall span in different ways based on how you set the Span (Hz) parameter.
Tunable: Yes
Programmatic Use
Block
Parameter:
FrequencyOffset |
Type:
double |
Configuration > Spectrum Analyzer Settings ( )
)
The number of input ports to the block, specified as an integer between 1 and 96. To change the number of input ports, drag a new input signal line to the block and the block automatically creates new ports.
Programmatic Use
Block Parameter:
NumInputPorts |
| Type: character vector or string scalar |
| Values: scalar between 1 and 96 |
Select this parameter to automatically open the Spectrum Analyzer window when you run the simulation.
Programmatic Use
Block Parameter:
OpenAtSimulationStart |
| Type: logical |
Since R2024b
Specify the precision of numeric values in the scope display as a positive integer in the range [1, 15].
Tunable: Yes
Specify the y-axis label in the Spectrum display as
a character vector or a string scalar. To display signal units, add
(%<SignalUnits>) to the label. When
simulation starts, Simulink replaces (%SignalUnits) with the units
associated with the signals.
For example, for a velocity signal with units of m/s enter
Velocity (%<SignalUnits>)
Tunable: Yes
Dependency
To enable this parameter, select Spectrum in the Scope tab.
Programmatic Use
Block Parameter:
YLabel |
| Type: character vector or string scalar |
Specify the y-axis limits in the Spectrum Analyzer
display as a two-element numeric vector of the form [ymin
ymax]. The units of the y-axis limits
depend on the Spectrum Unit in the
Spectrum tab.
Tunable: Yes
Dependency
To enable this parameter, select Spectrum in the Scope tab.
Programmatic Use
Block Parameter:
YLimits |
Type:
double |
Specify the display title. Enter %<SignalLabel>
to use the signal labels in the Simulink model as the axes titles.
Tunable: Yes
Programmatic Use
Block
Parameter:
Title |
| Type: character vector or string |
Select this check box to show the grid in the Spectrum Analyzer display.
Tunable: Yes
Programmatic Use
Block
Parameter:
ShowGrid |
Type:
logical |
Select a valid colormap name for the spectrogram, or enter a
three-column matrix with values in the range [0,1] defining RGB
triplets. For more information about colormaps, see colormap.
Tunable: Yes
Dependency
To enable this parameter, select Spectrogram in the Scope tab.
Programmatic Use
Block Parameter:
Colormap |
| Type: character vector or string scalar |
Specify the color limits of the spectrogram as a two-element numeric
vector of the form [colorMin colorMax]. The units of
the color limits directly depend upon the Spectrum
Unit in the Spectrogram tab.
Tunable: Yes
Dependencies
To enable this parameter, select Spectrogram in the Scope tab.
Programmatic Use
Block Parameter:
ColorLimits |
Type:
double |
Specify whether to display a Line or
Stem plot in the Spectrum display.
You can individually control the type of plot for each channel. To control the type of plot for each channel, select the channel and set the Plot Type parameter accordingly. (since R2025a)
Tunable: Yes
Dependency
To enable this parameter:
Select Spectrum in the Scope tab.
Select the Normal Trace check box in the Spectrum tab.
Programmatic Use
Block Parameter:
PlotType |
| Type: character vector or string scalar |
Specify the font size of the ticks, labels, title, and measurements of the scope as a positive scalar.
Tunable: Yes
Programmatic Use
Block Parameter: - |
| Type: double |
Specify the background color in the scope figure.
Tunable: Yes
Specify the background color of the axes.
Tunable: Yes
Specify the color of the labels, grid, and the channel names in the legend.
Tunable: Yes
Specify the channel for which you want to modify the visibility, line color, style, width, and marker properties.
Tunable: Yes
Select this check box to display the channel you have selected. If you clear this check box, the selected channel is no longer visible. You can also click the signal name in the legend to control its visibility. For more details, see Legend.
Tunable: Yes
Specify the line style for the selected channel.
Tunable: Yes
Specify the line width for the selected channel.
Tunable: Yes
Specify a data point marker for the selected channel. This parameter is similar to the Marker property for plots. You can choose any of the marker symbols from the drop-down list.
Tunable: Yes
Specify the line color for the selected channel.
Tunable: Yes
Configuration
Click the Legend button to enable the spectrum analyzer to display the signal legend. The legend displays the signal names from the model. For signals with multiple channels, the scope appends a channel index after the signal name. Continuous signals have straight lines before their names and discrete signals have step-shaped lines.
You can control which signals are visible using the legend. To hide a
signal, in the scope legend, click the signal name. To display the
signal, click the signal name again. Alternatively, you can control
which signal is visible using the Visible parameter
in the Spectrum Analyzer Settings (![]() ).
).
To display only one signal and hide all other signals, right-click the name of the signal you want the scope to display. To show all signals, press Esc.
Note
The legend displays only the first 20 signals. You cannot view or control any additional signals from the legend.
Tunable: Yes
Dependency
To enable the Legend, select Spectrum in the Scope tab.
Programmatic Use
Block Parameter:
ShowLegend |
Type:
logical |
When you select the Colorbar button, the spectrum analyzer shows the color bar.
Tunable: Yes
Dependencies
To enable the Colorbar button, select Spectrogram in the Scope tab.
Programmatic Use
Block Parameter:
ShowColorbar |
Type:
logical |
Stack axes vertically or horizontally by selecting the appropriate configuration in the layout grid.
Tunable: Yes
Dependencies
To enable the Layout, select Spectrum and Spectrogram in the Scope tab.
Programmatic Use
Block Parameter:
AxesLayout |
| Type: character vector or string scalar |
Share
Click this button to copy the scope display to the clipboard. You can preserve the color in the display by selecting Preserve Colors in the Copy to Clipboard drop down.
When you copy the display to the clipboard using the Copy to Clipboard and the Print options in the Scope tab > Share section, select this parameter for the scope to preserve the colors.
To access Preserve Colors, click the drop-down arrow for Copy to Clipboard.
Tunable: Yes
Click this button to save the scope display as an image or a PDF or to print the display.
Estimation Tab
Domain
The domain of the input signal you want to visualize. If you visualize time-domain signals, the scope transforms the signal to the frequency spectrum based on the algorithm you specify in the Estimation Method parameter.
Programmatic Use
Block Parameter:
InputDomain |
| Type: character vector or string scalar |
Set the frequency vector which determines the x-axis of the display to one of these values:
Auto— The scope calculates the frequency vector from the length of the input. For more details, see Frequency Vector.Input port— You specify the frequency vector at the Frequency input port on the block.Custom vector — You specify a custom vector as the frequency vector. The length of the custom vector must be equal to the frame size of the input signal.
Tunable: Yes
Dependency
To enable this parameter, set Input Domain to
Frequency.
Programmatic Use
Block Parameter:
FrequencyVectorSource,
FrequencyVector |
Type: character vector,
string scalar,
double |
Select the units of the frequency-domain input. This parameter enables the spectrum analyzer to scale frequency data when you select a different display unit in the Spectrum Unit parameter in the Estimation tab.
Tunable: Yes
Dependency
To enable this parameter, set Input Domain to
Frequency.
Programmatic Use
Block Parameter:
InputUnits |
| Type: character vector or string scalar |
Frequency Resolution
Select the spectrum estimation method as one of the following:
Filter Bank— Use an analysis filter bank to estimate the power spectrum. Compared to Welch's method, this method has a lower noise floor, better frequency resolution, lower spectral leakage, and requires fewer samples per update.Welch— Use Welch's method of averaged modified periodograms.
For more details on these methods, see Algorithms.
Tunable: Yes
Dependency
To use this parameter, set Input Domain to
Time.
Programmatic Use
Block Parameter:
Method |
| Type: character vector or string scalar |
Since R2024a
Specify the frequency resolution method of the spectrum analyzer as one of these options:
RBW— The RBW (Hz) parameter controls the frequency resolution (in Hz) of the analyzer.Number of frequency bands— Applies only when you set Estimation Method toFilter bank. The FFT Length parameter controls the frequency resolution.Window length— Applies only when you set Estimation Method toWelch. The Window Length parameter controls the frequency resolution.
Tunable: Yes
Dependency
To enable this parameter, set Input Domain to
Time.
Programmatic Use
Block Parameter:
FrequencyResolutionMethod |
| Type: character vector or string scalar |
Specify the sharpness of the prototype lowpass filter as a real nonnegative scalar in the range [0,1].
Increasing the filter sharpness decreases the spectral leakage and gives a more accurate power reading.
Tunable: Yes
Dependencies
To enable this parameter, set Estimation
Method to Filter
bank.
Programmatic Use
Block Parameter:
FilterSharpness |
Type:
double |
Specify the resolution bandwidth in Hz. This parameter defines the smallest positive frequency
that can be resolved by the scope. By default, this parameter is set to
Auto. In this case, the spectrum analyzer determines the
appropriate value to ensure that there are 1024 RBW intervals over the specified
frequency span.
If you set this parameter to Input port, you can specify
the RBW value through an input port on the block.
If you set this parameter to a numeric value, the value must allow at least two RBW intervals over the specified frequency span. In other words, the ratio of the overall frequency span to RBW must be greater than two:
To display this property on the status bar, click the
icon in the status bar and select RBW.
Programmatic Use
Block Parameter: RBWSource, RBW |
Type: character vector, string scalar, double |
Tunable: Yes
Since R2024a
Specify the window length in samples as an integer greater than 2. The block uses the window length to compute the spectral estimates. This parameter controls the frequency resolution.
Tunable: Yes
Dependencies
To enable this parameter, set:
Estimation Method to
Welch.Resolution Method to
Window Length.
Programmatic Use
Block Parameter:
WindowLength |
Type:double |
Since R2024a
You can set the FFT length to one of these options:
Auto— The value of FFT length depends on the setting of the frequency resolution method. When you set:Resolution Method to
RBW, the FFT length equals the number of samples per update, Nsamples. For more details on Nsamples, see the Algorithms section.Resolution Method to
Window length, the FFT length equals the value you specify in the Window length parameter or 1024, whichever is larger.Resolution Method to
Number of frequency bands, the FFT length equals the input frame size (number of rows).
Positive integer — The number of FFT points equals the value you specify in the
FFTLengthproperty.
Tunable: Yes
Dependencies
To enable this parameter, set:
Estimation Method to
Welch.Estimation Method to
Filter bankand Resolution Method toNumber of frequency bands.
Programmatic Use
Block Parameter:
|
Type:character vector
or string scalar, double |
Averaging
Specify the smoothing method as one of these:
VBW— Video bandwidth method. The block uses a lowpass filter to smooth the trace and decrease the noise. Use the VBW (Hz) parameter to specify the video bandwidth (VBW) value.Exponential— Weighted average of samples. The block computes the average over samples weighted by an exponentially decaying forgetting factor. Use the Forgetting Factor parameter to specify the weighted forgetting factor.Running— Running average of the last Q samples. Use the Spectral Averages parameter to specify Q. (since R2025a)
For more information on the averaging methods, see Averaging Method.
Tunable: Yes
Dependency
To enable this parameter, set Input Domain to
Time.
Programmatic Use
Block Parameter:
AveragingMethod |
| Type: character vector or string scalar |
Specify the video bandwidth as one of the following: S
Auto— The spectrum analyzer adjusts the VBW such that the equivalent forgetting factor is 0.9.Input portYou specify the frequency vector at the VBW input port on the block.Positive scalar — You specify a positive scalar. The spectrum analyzer adjusts the VBW using this value. The value you specify must be less than or equal to Sample Rate (Hz)/2.
For more details on the video bandwidth method, see Averaging Method.
The spectrum analyzer shows the VBW value in the status bar at the
bottom of the display. To display the VBW value, click the
icon in the status bar and select VBW.
Dependency
To enable this parameter, set:
Input Domain to
Time.Averaging MethodtoVBW.
Programmatic Use
Block Parameter:
VBWSource,
VBW |
Type:
double |
Tunable: Yes
Specify the forgetting factor of the exponential weighted averaging method as a scalar in the range [0,1].
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Averaging Method to
Exponential.
Programmatic Use
Block Parameter:
ForgettingFactor |
Type:
double |
Since R2025a
Specify the number of spectral averages Q as a positive integer.
The spectrum analyzer computes the current power spectrum estimate by computing a running average of the last Q power spectrum estimates.
Dependency
To enable this parameter, set:
Input Domain to
Time.Averaging Method to
Running.
Programmatic Use
Block Parameter:
SpectralAverages |
Type:
double |
Data Types: double
Frequency Options
Specify the frequency span mode as one of the following:
Full— The spectrum analyzer computes and plots the spectrum over the entire Nyquist Frequency Interval.Span and Center Frequency— The spectrum analyzer computes and plots the spectrum over the interval specified by the Span (Hz) and Center Frequency (Hz) parameters.Start and Stop Frequencies— The spectrum analyzer computes and plots the spectrum over the interval specified by the Start Frequency (Hz) and Stop Frequency (Hz) parameters.
Tunable: Yes
Dependency
To enable this parameter, set Input Domain to
Time.
Programmatic Use
Block Parameter:
FrequencySpan |
| Type: character vector or string scalar |
Specify the frequency span in Hz over which the spectrum analyzer computes and plots the spectrum. The overall span, defined by this parameter and the Center Frequency (Hz) parameter, must fall within the Nyquist Frequency Interval. This parameter defines the range of the values shown on the Frequency axis in the spectrum analyzer window.
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Frequency Span to
Span and Center Frequency.
Programmatic Use
Block Parameter:
Span |
Type:
double |
Specify the center of the frequency span in Hz over which the spectrum analyzer computes and plots the spectrum. Use this parameter with the Span (Hz) parameter to define the frequency span around a center frequency. This parameter defines the midpoint of the Frequency axis in the spectrum analyzer window.
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Frequency Span to
Span and Center Frequency.
Programmatic Use
Block Parameter:
CenterFrequency |
Type:
double |
Specify the starting frequency in Hz of the frequency interval over which the spectrum analyzer computes and plots the spectrum. The overall span, which is defined by this parameter and the Stop Frequency (Hz) parameter, must fall within the Nyquist Frequency Interval. This parameter defines the leftmost value on the Frequency axis in the spectrum analyzer window.
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Frequency Span to
Start and Stop Frequencies.
Programmatic Use
Block Parameter:
StartFrequency |
Type:
double |
Specify the stop frequency in Hz of the frequency interval over which the spectrum analyzer computes and plots the spectrum. The overall span, which is defined by this parameter and the Start Frequency (Hz) parameter, must fall within the Nyquist Frequency Interval. This parameter defines the rightmost value on the Frequency axis in the spectrum analyzer window.
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Frequency Span to
Start and Stop Frequencies.
Programmatic Use
Block Parameter:
StopFrequency |
Type:
double |
Window Options
Specify the windowing method to apply to the spectrum. Windowing is used to control the effect of sidelobes in spectral estimation. The window you specify affects the window length required to achieve a resolution bandwidth and the required number of samples per update. For more information about windowing, see Windows.
You can use your own spectral estimation window by directly specifying a custom window function name in the Window parameter.
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Estimation Method to
Welch.
Programmatic Use
Block Parameter:
Window,
CustomWindow |
| Type: character vector or string scalar |
Specify the sidelobe attenuation in dB as a scalar greater than or
equal to 45.
Tunable: Yes
Dependency
To enable this parameter, set Window to
Chebyshev or
Kaiser.
Programmatic Use
Block Parameter:
SidelobeAttenuation |
Type:
double |
Specify the percentage of overlap between the previous and the current buffered data segments as a scalar in the range [0 100). The overlap creates a window segment that the scope uses to compute a spectral estimate. The value must be greater than or equal to zero and less than 100.
Tunable: Yes
Dependency
To enable this parameter, set:
Input Domain to
Time.Estimation Method to
Welch.
Programmatic Use
Block Parameter:
OverlapPercent |
Type:
double |
Measurements Tab
Note
To access the phase noise measurement settings, you must have a valid Mixed-Signal Blockset™ license.
Channel
The channel for which you need to obtain measurements, specified as a positive integer in the range [1 N], where N is the number of input channels.
Tunable: Yes
Dependency
To enable this parameter, pass some data through the scope.
Programmatic Use
See MeasurementChannel.
Cursors
Click the Data Cursors button to enable data cursor measurements. Each cursor tracks a vertical line along the signal. The scope displays the difference between x- and y-values of the signal at the two cursors in the box between the cursors.
Tunable: Yes
Programmatic Use
See Enabled.
Select this parameter to position the cursors on the signal data points.
Tunable: Yes
Programmatic Use
See SnapToData.
Select this parameter to lock the frequency difference between the two cursors.
Tunable: Yes
Programmatic Use
See LockSpacing.
Peaks
Click the Peak Finder button to enable peak finder measurements. An arrow appears on the plot at each maxima and a Peaks panel appears at the bottom of the scope window.
Tunable: Yes
Programmatic Use
See Enabled.
Specify the maximum number of peaks to show as a positive integer less than 100.
Tunable: Yes
Programmatic Use
See NumPeaks.
Specify the level above which the scope detects peaks as a real scalar.
Tunable: Yes
Programmatic Use
See MinHeight.
Specify the minimum number of samples between adjacent peaks as a positive integer.
Tunable: Yes
Programmatic Use
See MinDistance.
Specify the minimum difference between the height of the peak and its neighboring samples as a nonnegative scalar.
Tunable: Yes
Programmatic Use
See Threshold.
Click the Label Peaks button to label the peaks. The scope displays the labels (P1, P2, …) above the arrows in the plot.
Tunable: Yes
Programmatic Use
See LabelPeaks.
Distortion
Click the Distortion button to enable distortion measurements. A Distortion panel appears at the bottom of the scope window when you click this button.
Tunable: Yes
Programmatic Use
See Enabled.
Specify the type of measurement data to display as Harmonic or Intermodulation. For more details, see Distortion Measurements.
Tunable: Yes
Programmatic Use
See Type.
Specify the number of harmonics to measure as a positive integer less than or equal to 99.
Tunable: Yes
Dependency
To enable this parameter, set Distortion Type to Harmonic.
Programmatic Use
See NumHarmonics.
When you select this parameter, the spectrum analyzer adds numerical labels to harmonics in the spectrum display.
Tunable: Yes
Programmatic Use
See LabelValues.
When you select this parameter, the spectrum analyzer adds numerical labels to the first-order intermodulation product and third-order frequencies in the spectrum analyzer display.
Tunable: Yes
Programmatic Use
See LabelValues.
Phase Noise
Click the Phase Noise button to enable phase noise measurements. A Phase Noise axis and Phase Noise panel appear in the scope window when you click this button.
Note
To access the phase noise measurement settings, you must have a valid Mixed-Signal Blockset license.
Tunable: Yes
Programmatic Use
See Enabled.
Specify the frequency offsets in Hz at which the scope measures the phase noise as a numeric vector with monotonically increasing values.
Tunable: Yes
Programmatic Use
See FrequencyOffset.
Select this parameter to plot the target phase noise profile. You can specify this profile in the Target Phase Noise (dBc/Hz) parameter.
Tunable: Yes
Programmatic Use
See PlotTargetPhaseNoise.
Specify the target phase noise profile in dBc/Hz as a numeric vector of the same length as the Frequency Offsets (Hz) vector.
Tunable: Yes
Dependencies
To enable this parameter, select the Plot Target Phase Noise parameter.
Programmatic Use
See TargetPhaseNoise.
Select this parameter to label the measured phase noise on the plot.
When you select this parameter, the spectrum analyzer labels the
measured phase noise values on the plot as SN1,
SN2, and so on.
Tunable: Yes
Programmatic Use
See LabelPhaseNoise.
Spectrum Tab
Note
This tab appears when you select Spectrum in the Scope tab.
Trace Options
Select this check box to enable a two-sided spectrum view. In this view, the spectrum analyzer shows both negative and positive frequencies. When the input signal is complex-valued, you must select this parameter. If you clear this check box, the spectrum analyzer shows a one-sided spectrum with positive frequencies only. In this case, the input signal data must be real valued.
When you clear this check box, the spectrum analyzer uses power folding.
The y-axis values are twice the amplitude that they
would be if you were to select this parameter, except at
0 and the Nyquist frequency. A one-sided
power spectral density (PSD) contains the total power of the signal in
the frequency interval from DC to half the Nyquist rate. For more
information, see pwelch.
Tunable: Yes
Programmatic Use
Block
Parameter:
PlotAsTwoSidedSpectrum |
Type:
logical |
When you select this check box, the spectrum analyzer calculates and plots the power spectral estimates. The spectrum analyzer performs a smoothing operation by averaging several spectral estimates and continues its spectral computations even when you clear this parameter.
Tunable: Yes
Dependencies
To clear this check box, first select either the Max-Hold Trace or the Min-Hold Trace parameters.
To enable this parameter, select Spectrum in the Scope tab.
Programmatic Use
Block Parameter:
PlotNormalTrace |
Type:
logical |
Select this check box to enable the spectrum analyzer to plot the maximum spectral values of all the estimates. The spectrum analyzer computes the maximum-hold spectrum at each frequency bin by keeping the maximum value of all the power spectrum estimates. When you clear this check box, the spectrum analyzer resets its maximum-hold computations.
Tunable: Yes
Dependency
To enable this parameter, select Spectrum in the Scope tab.
Programmatic Use
Block Parameter:
PlotMaxHoldTrace |
Type:
logical |
Select this check box to enable the spectrum analyzer to plot the minimum spectral values of all the estimates. The spectrum analyzer computes the minimum-hold spectrum at each frequency bin by keeping the minimum value of all the power spectrum estimates. When you clear this check box, the spectrum analyzer resets its minimum-hold computations.
Tunable: Yes
Dependency
To enable this parameter, select Spectrum in the Scope tab.
Programmatic Use
Block Parameter:
PlotMinHoldTrace |
Type:
logical |
Scale
Specify the scale to display frequencies as
Linear or Log.
When the frequency span contains negative frequency values, you cannot
choose the logarithmic option.
Tunable: Yes
Dependency
To set the Frequency Scale to
Log, clear the Two-Sided
Spectrum check box in the Trace
Options section in the Spectrum
or the Spectrogram tab (if enabled). If you
select the Two-Sided Spectrum check box, then
the Frequency Scale parameter is set to
Linear.
Programmatic Use
Block Parameter:
FrequencyScale |
| Type: character vector or string scalar |
Specify the reference load in ohms that the Spectrum Analyzer uses as a reference to compute the power values.
Tunable: Yes
Dependency
To enable this parameter, set:
Spectrum type to
PowerorPower Density.Spectrum Unit to any option other than
dBFSordBFS/Hz.
Programmatic Use
Block
Parameter:
ReferenceLoad |
Type:
double |
Specify the units in which the spectrum analyzer displays the power values as one of the following:
dBmdBFSdBuV(since R2023b)dBVdBWVrmsWattsdBm/HzdBW/HzdBFS/HzWatts/HzAuto
Tunable: Yes
Dependency
The units available depend on the value you choose for the Spectrum parameter in the Scope tab.
| Estimation tab > Input Domain parameter | Scope tab > Spectrum option | Available Units |
|---|---|---|
Time | Power | dBm,
dBW,
dBFS,
Watts |
Power
Density | dBm/Hz,
dBW/Hz,dBFS/Hz,
Watts/Hz | |
RMS | dBuV (since R2023b),
dBV,
Vrms | |
Frequency | ― | Auto,
dBm, dBuV (since R2023b),
dBV,
dBW,
Vrms,
Watts |
If you set the Input Domain parameter to
Frequency and the Spectrum
Unit parameter to Auto,
the spectrum analyzer assumes the spectrum units to be equal to
input units specified in the Estimation tab >
Input Unit parameter. If you set the
Input Domain parameter to
Time and the Spectrum
Unit parameter to any option other than
Auto, the spectrum analyzer converts
the units specified in the Input Unit parameter
to the units specified in the Spectrum Unit
parameter.
Programmatic Use
Block Parameter:
SpectrumUnits |
| Type: character vector or string scalar |
The full scale used for the decibel full scale (dBFS) units. By default, the spectrum analyzer uses the entire spectrum scale. Specify a positive real scalar for the dBFS full scale.
Tunable: Yes
Dependencies
To enable this parameter:
In the Scope tab, set the spectrum type to
PowerorPower Density.In the Estimation tab, set Input Domain to
Time.In the Spectrum tab, set Spectrum Unit to
dBFSordBFS/Hz(when spectrum type is set toPower Density).
Programmatic Use
Block Parameter:
FullScale |
Type:
double |
Spectrogram Tab
Note
This tab appears when you select Spectrogram in the Scope tab.
Channel
Select the signal channel for which the spectrogram settings apply.
Tunable: Yes
Dependency
To enable this parameter, select Spectrogram in the Scope tab.
Programmatic Use
Block Parameter:
SpectrogramChannel |
Type: character vector,
string scalar, double |
Time Options
Time resolution is the amount of data, in seconds, used to compute a spectrogram line. The minimum attainable resolution is the amount of time it takes to compute a single spectral estimate. The tooltip displays the minimum attainable resolution given the current spectrum analyzer settings.
When you set RBW (Hz) and Time
Resolution (s) to Auto, then
the spectrum analyzer adjusts the RBW value such that there are 1024 RBW
intervals in one frequency span and sets the time resolution is set to
1/RBW.
When you set RBW (Hz) to
Auto and Time Resolution
(s) to a positive scalar, then time resolution becomes
the main control and RBW is set to 1/Time Resolution
(s) Hz.
When you set RBW (Hz) to a positive scalar and
Time Resolution (s) to
Auto, then RBW becomes the main control
and the time resolution is set 1/RBW (Hz) s.
When you set RBW (Hz) and Time Resolution (s) to a positive value, then time resolution must be equal to or larger than the minimum attainable time resolution defined by 1/RBW (Hz). Several spectral estimates are combined into one spectrogram line to obtain the desired time resolution. Interpolation is used to obtain time resolution values that are not integer multiples of 1/RBW (Hz).
Tunable: Yes
Dependency
To enable this parameter, select Spectrogram
in the Scope tab and set Input
Domain to Time in the
Estimation tab.
Programmatic Use
Block Parameter:
TimeResolutionSource,
TimeResolution |
Type: character vector,
string scalar, double |
The time span over which the spectrum analyzer displays the
spectrogram specified as a positive scalar in seconds. The time span is
the product of the desired number of spectral lines and the time
resolution. When you set this parameter to
Auto, the spectrogram displays 100
spectrogram lines at any given time. Otherwise, the spectrogram uses the
time duration you specify in this parameter. The time span that you
specify must be at least two times larger than the duration of the
number of samples required for a spectral update.
Tunable: Yes
Dependency
To enable this parameter, select Spectrogram
in the Scope tab and set Input
Domain to Time in the
Estimation tab.
Programmatic Use
Block Parameter:
TimeSpanSource,
TimeSpan |
Type: character vector,
string scalar, double |
For more information on Two-Sided Spectrum, see Spectrum Tab > Trace Options.
Spectral Mask Tab
Note
This tab appears when you select Spectrum in the
Scope tab and set the Spectrum
type to be Power or Power
Density.
Views
Select Upper Mask to display the upper mask in the spectrum plot. The Spectral Mask panel appears at the bottom of the spectrum analyzer window and displays mask details, such as number of times a mask succeeded, number of times a mask failed, channels causing the mask failure, and so on.
Use the Upper Limits parameter to specify the upper mask. If the entire spectrum plot is below the upper mask, the upper mask looks green. In all other cases, the upper mask looks red.
Tunable: Yes
Programmatic Use
See EnabledMasks.
Select Lower Mask to display the lower mask in the spectrum plot. The Spectral Mask panel appears at the bottom of the spectrum analyzer window and displays mask details, such as number of times a mask succeeded, number of times a mask failed, channels causing the mask failure, and so on.
Use the Lower Limits parameter to specify the lower mask. If the entire spectrum plot is above the lower mask, the lower mask looks green. In all other cases, the lower mask looks red.
Tunable: Yes
Programmatic Use
See EnabledMasks.
Configuration
Specify the limit for the upper spectral mask as a scalar or a two-column matrix.
If UpperMask is a scalar, the upper limit mask
uses the same power value for all frequencies specified in the spectrum
analyzer.
If you specify a matrix, the first column contains the frequency values (Hz), which correspond to the x-axis values. The second column contains the power values, which correspond to the associated y-axis values.
To apply offsets to the power and frequency values, use the Reference Level (dBr) and the Frequency Offset (Hz) parameters.
Tunable: Yes
Programmatic Use
See UpperMask.
Specify the limit for the lower spectral mask as a scalar or a two-column matrix.
If LowerMask is a scalar, the lower limit mask
uses the same power value for all frequencies specified in the spectrum
analyzer.
If you specify a matrix, the first column contains the frequency values (Hz), which correspond to the x-axis values. The second column contains the power values, which correspond to the associated y-axis values.
To apply offsets to the power and frequency values, use the Reference Level (dBr) and the Frequency Offset (Hz) parameters.
Tunable: Yes
Programmatic Use
See LowerMask.
Specify the reference level for mask power values as a numeric scalar
or set it to Spectrum peak.
When you set Reference Level (dBr) to a scalar value, the spectrum analyzer uses this value as the reference to the power values (in dBr) for the upper mask and the lower mask of the spectrum analyzer. The reference level should have the same units as the Spectrum Unit parameter in the Spectrum tab.
When you set Reference Level (dBr) to
Spectrum peak, the spectrum analyzer uses
the peak value of the current spectrum of the
Channel in the Spectral
Mask tab as the reference power value.
Tunable: Yes
Programmatic Use
See ReferenceLevel and CustomReferenceLevel.
Select the input channel which the spectrum analyzer uses to determine
the mask reference level. The peak value of the spectrum in this channel
becomes the mask reference level when you set the Reference
Level (dBr) parameter to Spectrum
peak.
Tunable: Yes
Dependency
To enable this parameter, set Reference Level
(dBr) to Spectrum peak and
display some data on the scope.
Programmatic Use
See SelectedChannel.
Specify the frequency offset in Hz as a finite numeric scalar. Using this value, the spectrum analyzer offsets the frequency values in the Upper Mask and the Lower Mask parameters.
Tunable: Yes
Programmatic Use
See MaskFrequencyOffset.
Channel Measurements Tab
Note
This tab appears when you select Spectrum in the Scope tab.
Channel
Specify the channel over which the spectrum analyzer computes and displays the occupied bandwidth and adjacent channel power ratio as a positive integer in the range [1 N], where N is the number of input channels.
Tunable: Yes
Dependency
To enable this parameter, pass data through the scope.
Programmatic Use
See MeasurementChannel.
Channel Measurements
Click Channel Measurements to enable channel measurements.
Tunable: Yes
Programmatic Use
See Enabled.
Specify the type of measurement data to display as
Occupied BW or
ACPR.
Tunable: Yes
Programmatic Use
See Type.
Specify the percentage of power over which the spectrum analyzer computes the occupied bandwidth as a positive scalar.
Tunable: Yes
Dependency
To enable this parameter, set Type to
Occupied BW.
Programmatic Use
See PercentOccupiedBW.
Frequency Options
Specify the frequency span mode as one of the following:
Span and Center Frequency— Measure over a frequency range specified in Span (Hz) and around the frequency value specified in Center Frequency (Hz).Start and Stop Frequencies— Measure over the frequency range [Start Frequency (Hz), Stop Frequency (Hz)].
Tunable: Yes
Programmatic Use
See FrequencySpan.
Specify the frequency span over which the spectrum analyzer computes the channel measurements as a positive scalar in Hz.
Tunable: Yes
Dependency
To enable this parameter, set Frequency Span
to Span and Center Frequency.
Programmatic Use
See Span.
Center frequency of the span over which the object computes the channel measurements, specified as a real scalar in Hz.
Tunable: Yes
Dependency
To enable this parameter, set Frequency Span
to Span and Center Frequency.
Programmatic Use
See CenterFrequency.
Specify the start frequency in Hz over which the spectrum analyzer computes the channel measurements.
Tunable: Yes
Dependency
To enable this parameter, set Frequency Span
to Start and Stop Frequencies.
Programmatic Use
See StartFrequency.
Specify the stop frequency in Hz over which the spectrum analyzer computes the channel measurements.
Tunable: Yes
Dependency
To enable this parameter, set Frequency Span
to Start and Stop Frequencies.
Programmatic Use
See StopFrequency.
Adjacent Channels
Specify the number of adjacent channel pairs as a positive integer in
the range [1, 12].
Tunable: Yes
Dependency
To enable this parameter, set Type to
ACPR.
Programmatic Use
See NumOffsets.
Specify the frequency of the adjacent channel relative to the center frequency of the main channel as a real vector of length equal to the number of offset pairs specified in Num Pairs.
Tunable: Yes
Dependency
To enable this parameter, set Type to
ACPR.
Programmatic Use
See ACPROffsets.
Specify the adjacent channel bandwidth in Hz as a positive scalar.
Tunable: Yes
Dependency
To enable this parameter, set Type to
ACPR.
Programmatic Use
See AdjacentBW.
Specify the filter shape for the main and adjacent channels as
None, RRC, or
Gaussian.
Tunable: Yes
Dependency
To enable this parameter, set Type to
ACPR.
Programmatic Use
See FilterShape.
Specify the roll-off factor as a real scalar in the range
[0, 1].
Tunable: Yes
Dependency
To enable this parameter, set Type to
ACPR and Filter
Shape to RRC.
Programmatic Use
See FilterCoeff.
Specify the BT product as a real scalar in the range
[0, 1].
Tunable: Yes
Dependency
To enable this parameter, set Type to
ACPR and Filter
Shape to Gaussian.
Programmatic Use
See FilterCoeff.
Property Inspector Only
Input channel names, specified as a character vector, string, or array. The names appear in
the legend, Settings, and Measurements
panels. If you do not specify the names, the scope labels the channels as
Channel 1, Channel 2, etc.
Example: ["A","B"]
Dependency
To see channel names, select Legend in the Scope tab.
Programmatic Use
Block Parameter: ChannelNames |
| Type: cell array of character vectors or string array |
Auto— If you have not specified Title and Y-Label, the scope maximizes all plots.On— The scope maximizes all plots and hides all values in Title and Y-label.Off— The scope does not maximize plots.
Hover over the Spectrum Analyzer to see the maximize axes button
![]() .
.
Tunable: Yes
Programmatic Use
Block Parameter:
MaximizeAxes |
| Type: character vector or string scalar |
OnceAtStop— Scale y-axis after simulation completes.Manual— Manually scale y-axis range with the Scale Y-axis Limits toolbar button.Auto— Scale y-axis range during and after simulation.Updates— Scale y-axis after the number of time steps specified in the Number of Updates text box (100by default). Scaling occurs only once during each run.
Tunable: Yes
Programmatic Use
Block Parameter: AxesScaling |
| Type: character vector or string scalar |
Set this property to delay auto scaling the y-axis.
Tunable: Yes
Dependency
To enable this property, set Axes Scaling to Updates.
Programmatic Use
Block Parameter: AxesScalingNumUpdates |
| Type: character vector or string scalar |
| Values: scalar |
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Measure signal values using vertical waveform cursors that track along the signal.
When you click the Data Cursors button in the Measurements tab of the Spectrum Analyzer, the spectrum display shows vertical cursors on each signal. Each cursor tracks a vertical line along the signal. The scope displays the difference between x- and y-values of the signal at the two cursors in the box between the cursors.
To enable cursor measurements, click the Data Cursors button in the Measurements tab. The cursors appear only when the Spectrum Analyzer has at least one signal in its display.
You can use the mouse to move the vertical cursors left and right.
In the Measurements tab, click the Data Cursors drop-down arrow to select one of these options:
Snap to Data — To position the cursors on the signal data points.
Lock Cursor Spacing — To lock the frequency difference between the two cursors.
For modifying the cursor measurements programmatically, see the CursorMeasurementsConfiguration
object.
Compute and display peak values in the scope display.
When you click the Peak Finder button in the Measurements tab of the Spectrum Analyzer, an arrow appears on the plot at each maxima and a Peaks panel appears at the bottom of the scope window. The Spectrum Analyzer computes peaks from the portion of the input signal that is currently on display in the scope, and the Peaks panel shows the peak values and the frequencies at which they occur.
The Peaks section in the Measurements tab allows you to specify the number of peaks you want the scope to display, the minimum height above which you want the scope to detect peaks, the minimum distance between peaks, and label the peaks.
The Spectrum Analyzer algorithm defines a peak as a local maximum with lower values present on either side of the peak. It does not consider end points as peaks. For more information on the algorithm, see the findpeaks function.
The peaks are valid for any units of the input signal. The letter after the value associated with each measurement indicates the abbreviation for the appropriate International System of Units (SI) prefix, such as m for milli-. For example, if the input signal is measured in volts, an m next to a measurement value indicates that this value is in units of millivolts.
For modifying the peak finder measurements programmatically, see the PeakFinderConfiguration object. For more information on these settings in the
UI, see Peaks.
Measure harmonic distortion and intermodulation distortion.
When you click the Distortion button in the Distortion section of the Measurements tab, a distortion panel opens at the bottom of the Spectrum Analyzer window. This panel shows the harmonic and distortion measurement values for the input signal currently on display in the scope. The Distortion section in the Measurements tab allows you to specify the distortion type, number of harmonics, and even label the harmonics.
Note
For an accurate measurement, ensure that the fundamental signal (for harmonics) or
primary tones (for intermodulation) is larger than any spurious or harmonic content. To
do so, you may need to adjust the resolution bandwidth (RBW) of the
Spectrum Analyzer. Make sure that the bandwidth is low enough to isolate the signal and
harmonics from spurious noise content. In general, you should set the RBW value such
that there is at least a 10 dB separation between the peaks of the sinusoids and the
noise floor. You also might need to select a different spectral window to obtain a valid
measurement.
You can set the Distortion Type parameter to one of these values:
Harmonic–– SelectHarmonicif your input is a single sinusoid.Intermodulation–– SelectIntermodulationif your input is two equal-amplitude sinusoids. Intermodulation can help you determine distortion when the scope uses only a small portion of the available bandwidth.
See Distortion Measurements for information on how distortion measurements are calculated.
When you set the Distortion Type to Harmonic,
these fields appear in the Harmonic Distortion panel at the bottom
of the Spectrum Analyzer window.
H1 — Fundamental frequency in Hz and its power in decibels of the measured power referenced to 1 milliwatt (dBm).
H2, H3, ... — Harmonics frequencies in Hz and their power in decibels relative to the carrier (dBc). If the harmonics are at the same level or exceed the fundamental frequency, reduce the input power.
THD — Total harmonic distortion. This value represents the ratio of the power in the harmonics D to the power in the fundamental frequency S. If the noise power is too high in relation to the harmonics, the THD value is not accurate. In this case, lower the resolution bandwidth or select a different spectral window.
SNR — Signal-to-noise ratio (SNR). This value represents the ratio of the power in the fundamental frequency S to the power of all nonharmonic content N, including spurious signals, in decibels relative to the carrier (dBc).
If you see
––as the reported SNR, the total nonharmonic content of your signal is less than 30% of the total signal.SINAD — Signal-to-noise-and-distortion ratio. This value represents the ratio of the power in the fundamental frequency S to all other content (including noise N and harmonic distortion D) in decibels relative to the carrier (dBc).
SFDR — Spurious-free dynamic range (SFDR). This value represents the ratio of the power in the fundamental frequency S to power of the largest spurious signal R regardless of where it falls in the frequency spectrum. The worst spurious signal might or might not be a harmonic of the original signal. SFDR represents the smallest value of a signal that can be distinguished from a large interfering signal. SFDR includes harmonics.
The harmonic distortion measurement automatically locates the largest sinusoidal component (fundamental signal frequency). It then computes the harmonic frequencies and power in each harmonic in your signal and ignores any DC component. The measurement does not include any harmonics that are outside the Spectrum Analyzer frequency span. Adjust your frequency span so that it includes all the desired harmonics.
Note
To view the best harmonics, make sure that your fundamental frequency is set high enough to resolve the harmonics. However, this frequency should not be so high that aliasing occurs. For the best display of harmonic distortion, your plot should not show skirts, which indicate frequency leakage. The noise floor should be visible.
For a better display, try a Kaiser window with a large sidelobe attenuation (e.g. between 100–300 db).


When you set the Distortion Type to
Intermodulation, the following fields appear in the
Intermodulation Distortion panel at the bottom of the Spectrum
Analyzer window.
F1 — Lower fundamental first-order frequency.
F2 — Upper fundamental first-order frequency.
2F1 - F2 — Lower intermodulation product from third-order harmonics.
2F2 - F1 — Upper intermodulation product from third-order harmonics.
TOI — Third-order intercept point. If the noise power is too high in relation to the harmonics, the TOI value will not be accurate. In this case, you should lower the resolution bandwidth or select a different spectral window. If the TOI has the same amplitude as the input two-tone signal, reduce the power of that input signal.
The intermodulation distortion measurement automatically locates the fundamental and the first-order frequencies (F1 and F2). It then computes the frequencies of the third-order intermodulation products (2F1−F2 and 2F2−F1).
For modifying the distortion measurements programmatically, see the DistortionMeasurementsConfiguration object. For more information on these
settings in the UI, see Distortion.
Measure the occupied bandwidth or adjacent channel power ratio (ACPR).
When you click the Channel Measurements button in the Channel Measurements tab, a channel measurements panel opens at the bottom of the Spectrum Analyzer window. This panel displays the occupied bandwidth or the adjacent channel power ratio measurements. In the Channel Measurements tab, you can specify the occupied bandwidth or the ACPR settings, frequency span, center frequency, and start and stop frequencies.
You can select the channel measurements Type to:
Occupied BW–– Occupied bandwidthACPR–– Ratio of the power of the main channel to the power of the adjacent channel
For more details on how the Spectrum Analyzer calculates the occupied bandwidth, see Occupied BW.
Occupied Bandwidth
When you set the Type of channel measurement to compute and display to
Occupied BW, these fields appear in the measurements panel at
the bottom of the scope window.
Channel Power — Total power in the channel
Occupied BW — Bandwidth containing the specified Occupied BW (%) of the total power of the spectrum.
Frequency Error — Difference between the center of the occupied band and the center frequency (Center Frequency (Hz)) of the channel
ACPR
When you set the Type of channel measurement to compute and display to
ACPR, these fields appear in the measurements panel at the
bottom of the scope window.
Lower (Rel Power (dBc)) — Ratio of the power of the lower sideband to the power of the main channel
Upper (Rel Power (dBc)) — Ratio of the power of the upper sideband to the power of the main channel
To modify the channel measurements programmatically, see the ChannelMeasurementsConfiguration object. For more information on these
settings in the UI, see Channel Measurements.
Visualize spectrum limits and compare spectrum values to specification values.
Add upper and lower masks to the Spectrum Analyzer to visualize spectrum limits and compare spectrum values to specification values. To enable the Spectral Mask tab, select Spectrum in the Scope tab. When you click the Upper Mask and Lower Mask buttons in the Spectral Mask tab, a Spectral Mask panel opens at the bottom of the Spectrum Analyzer window. This panel provides information on pass-fail statistics of masks, names of masks currently failing or passing, and names of channels causing the failure.
You can modify the mask settings in the Spectral Mask tab. For more
information on these settings in the UI, see Spectral Mask. For
modifying the channel measurements programmatically, see the SpectralMaskConfiguration object.
You can check the status of the spectral mask using the getSpectralMaskStatus function. This function gives details on the number
of times a mask succeeded or failed, names of channels causing mask failure, and so
on.
You can even use the MaskTestFailed event to perform an action every time
the mask fails. To trigger a function when the mask fails, create a listener to the
MaskTestFailed event and define a callback function to trigger
it. For more details about using events, see Events.
Set configuration and style settings in the Spectrum Analyzer.
To control the settings of the display and labels, color and styling, click on
Settings (![]() ) in the Scope tab of the Spectrum
Analyzer toolstrip.
) in the Scope tab of the Spectrum
Analyzer toolstrip.
In the dialog box that opens, you can customize the font size, plot type, y-axis properties of the spectrum plot, and color map properties of the spectrogram plot. You can change the color of the spectrum plot, background, axes, and labels and also change the line properties.
When you view the spectrum or the spectrogram, you see only the relevant options. For more details about these options, see Configuration > Spectrum Settings.
Zoom and pan axes using display controls.
To scale the plot axes, use the mouse to pan around the axes and the scroll button on your mouse to zoom in and out of the plot. Additionally, you can use the buttons that appear when you hover over the plot window.
 — Maximize the axes, hide all labels and inset
the axes values.
— Maximize the axes, hide all labels and inset
the axes values. — Zoom in on the plot.
— Zoom in on the plot. — Pan the plot.
— Pan the plot. — Autoscale the axes to fit the shown data.
— Autoscale the axes to fit the shown data.
Tips
If you set the Averaging Method to VBW
or Exponential, and you introduce NaN or
Inf values into the data, the spectrum appears blank. To ignore
the NaN or Inf values:
In the Home tab > Environment section of the MATLAB® toolstrip, click Settings (
 ).
).In the Workspace section of the Settings dialog box, select the Ignore NaNs when calculating statistics check box.
Algorithms
When you choose the Filter Bank method, the spectrum
analyzer uses an analysis filter bank to estimate the power spectrum.
The filter bank splits the broadband input signal x(n), of sample rate fs, into multiple narrow band signals y0(m), y1(m), … , yM-1(m), of sample rate fs/M.
The variable M represents the number of frequency bands in the
filter bank. In the spectrum analyzer, M is equal to the number of
data points needed to achieve the specified RBW value or 1024, whichever is larger. For
more information on the analysis filter bank and its implementation, see the More About and the Algorithm sections in the
dsp.Channelizer object.
After the spectrum analyzer splits the broadband input signal into multiple narrow bands, it computes the power in each narrow frequency band using the following equation. Each Zi value is the power estimate over that narrow frequency band.
L is length of the narrowband signal yi(m) and i = 1, 2, …, M−1.
The power values in all the narrow frequency bands (denoted by Zi) form the Z vector.
The spectrum analyzer averages the current Z vector with the previous Z vectors using one of the moving average methods: video bandwidth, exponential weighting, or running. The output of the averaging operation forms the spectral estimate vector. For details on the two averaging methods, see Averaging Method.

The spectrum analyzer uses the value you specify in the RBW (Hz) parameter or the Number of frequency bands parameter to determine the input frame length.
When you specify the Resolution Method to
RBW, and you set RBW (Hz) to:
Auto–– The spectrum analyzer determines the appropriate resolution bandwidth to ensure that there are 1024 RBW intervals over the specified frequency span. When you set RBW (Hz) toAuto, the spectrum analyzer calculates RBW using this equation.scalar value –– The spectrum analyzer calculates the number of samples Nsamples using this equation.
Fs is the sample rate of the input signal as specified in the Sample Rate (Hz) property.
The RBW value you specify must be such that there are at least two RBW intervals over the specified frequency span. The ratio of the overall span to RBW must be greater than two.
span is the frequency span over which the spectrum analyzer computes and plots the spectrum. To view the Span (Hz) in the scope, click the Estimation tab on the spectrum analyzer toolstrip and navigate to the Frequency Options section. To enable this property, set Frequency Span to
Span and Center Frequency.
When you specify the Resolution Method to Number of
frequency bands, the resulting RBW is given by:
When the number of input samples is not sufficient to achieve the specified resolution bandwidth, the spectrum analyzer adjusts its RBW value according to the number of input samples provided and displays a message similar to this one. The spectrum analyzer removes this message once you provide enough input samples.

When you select the Welch method, the power spectrum estimate is
the averaged modified periodograms.
The algorithm in the spectrum analyzer consists of these steps:
The block buffers the input into N-point data segments. Each data segment is split into P overlapping data segments, each of length M, overlapping by D points. The data segments can be represented as:
If D = M/2, the overlap is 50%.
If D = 0, the overlap is 0%.
Apply a window to each of the P overlapping data segments in the time domain.
If you set the Resolution Method to
Window length, you can specify the data window length Nwindow using the Window Length parameter in the Estimation tab.If you set the Resolution Method to
RBW, the algorithm determines the data window length using this equation, .Then, it partitions the input signal into a number of windowed data segments.
Most window functions afford more influence to the data at the center of the set than to the data at the edges, which represents a loss of information. To mitigate that loss, the individual data sets are commonly overlapped in time. For each windowed segment, compute the periodogram by computing the discrete Fourier transform. Then compute the squared magnitude of the result and divide the result by M.
where U is the normalization factor for the power in the window function and is given by
You can specify the window using the Window parameter in the Estimation tab of the spectrum analyzer toolstrip.
The spectrum analyzer calculates and plots the power spectrum, power spectrum density, and RMS using the modified Periodogram estimator. For more information about the Periodogram method, see
periodogram.To determine the power spectrum estimate for Welch's method, the spectrum analyzer averages the result of the periodograms for the last P data segments. The averaging reduces the variance, compared to the original N-point data segment. For more details on the averaging, see Averaging Method.
The spectrum analyzer computes the power spectral density using:
The power spectrum is the product of the power spectral density and the resolution bandwidth, as given by this equation.
The spectrum analyzer plots the power as a spectrogram in the Spectrogram mode. Each line of the spectrogram is one periodogram. The time resolution of each line is 1/RBW, which is the minimum attainable resolution. Achieving the resolution you want might require combining several periodograms. You then use interpolation to calculate noninteger values of 1/RBW. In the spectrogram display, time scrolls from top to bottom, so the most recent data appears at the top of the display. The offset shows the time value at which the center of the most current spectrogram line occurred.
The spectrum analyzer uses a certain number of samples to compute a spectral estimate. This value is directly related to the resolution bandwidth (RBW) using this equation,
or to the window length (Nwindow) using this equation,
where Op is the overlap percentage, NENBW is the normalized effective noise bandwidth, Fs is the input sample rate, and RBW is the resolution bandwidth.
The spectrum analyzer shows the number of samples per update in the spectrum analyzer status bar.
When you specify the Resolution
Method to RBW, the window length is given
by,
When you specify the Resolution
Method to Window length, the algorithm uses
the window length value you specify in the Window Length parameter
in the Estimation tab on the spectrum analyzer toolstrip.
The overlap percentage Op is the value you specify in the Overlap % property. To view the Overlap % in the scope, click the Estimation tab on the spectrum analyzer toolstrip and navigate to the Window Options section.
When you increase the overlap percentage, the spectrum analyzer needs fewer new input samples to compute a new spectral update.
| Op | Nsamples |
|---|---|
| 0% | 100 |
| 50% | 50 |
| 80% | 20 |
The normalized effective noise bandwidth NENBW is a window parameter that measures the noise performance of the window. NENBW is determined using the window length and the window coefficients, and is given by the following equation:
w(n) denotes the vector of window coefficients. Nwindow is the window length. For more information on how the algorithm determines the window length, see the Spectrum Estimation –– Welch's Method section in Algorithms.
The rectangular window has the smallest NENBW, with a value of 1. All other windows have a larger NENBW value. For example, the Hann window has an NENBW value of approximately 1.5.
The spectrum analyzer shows the value of NENBW in the spectrum analyzer status bar.
You can enable NENBW only when you set
Input Domain to Time and
Estimation Method to Welch in the
Estimation tab on the spectrum analyzer toolstrip.
Fs is the sample rate of the input signal.
To view the Sample Rate (Hz) in the scope, click the
Scope tab on the spectrum analyzer toolstrip and navigate to
the Bandwidth section. You can enable this property in the status
bar at the bottom of the spectrum analyzer window. Click the ![]() icon in the status bar and select
icon in the status bar and select Sample
Rate.
Resolution bandwidth controls the spectral resolution of the displayed signal. The RBW value determines the spacing between frequencies that the scope can resolve. A smaller value gives a higher spectral resolution and lowers the noise floor, that is, the spectrum analyzer can resolve frequencies that are closer to each other. However, this comes at the cost of a longer sweep time.
You can specify the resolution bandwidth using the RBW (Hz) parameter.
If you specify the window length, the scope determines the RBW value from the window length using this equation, .
When you specify the Resolution
Method to RBW, and you set RBW
(Hz) to:
Auto–– The spectrum analyzer determines the appropriate resolution bandwidth to ensure that there are 1024 RBW intervals over the specified frequency span. When you set RBW (Hz) toAuto, the spectrum analyzer calculates using this equation.scalar value –– Specify a value such that there are at least two RBW intervals over the specified frequency span. The ratio of the overall span to RBW must be greater than two:
span is the frequency span over which the spectrum analyzer
computes and plots the spectrum. Spectrum analyzer shows the span through the
Span (Hz) property. To view the Span (Hz)
in the scope, click the Estimation tab on the spectrum analyzer
toolstrip, navigate to the Frequency Options section, and set
Frequency Span to Span and Center
Frequency.
When you specify the Resolution
Method to Number of frequency bands, the
resulting RBW is given by:
When the number of input samples is not sufficient to achieve the specified resolution bandwidth, the spectrum analyzer adjusts its RBW value according to the number of input samples provided and displays a message similar to this one. The spectrum analyzer removes this message once you provide enough input samples.

You can enable this property in the status bar at the bottom of the spectrum analyzer
window. Click the ![]() icon in the status bar and select
icon in the status bar and select
RBW.
When you plot the two-sided spectrum by selecting Two-Sided Spectrum in the Spectrum or Spectrogram tab, the Nyquist frequency interval is Hz.
When you clear the Two-Sided Spectrum, the Nyquist frequency interval is Hz.
When you set Frequency (Hz) to Auto, the software calculates the frequency vector for the frequency-domain input.
When you plot the two-sided spectrum by selecting Two-Sided Spectrum in the Spectrum or Spectrogram tab, the frequency vector is:
When you clear the Two-Sided Spectrum, the frequency vector is:
The spectrum analyzer calculates Occupied BW using these steps.
Calculate the total power in the measured frequency range.
Determine the lower frequency value. Starting at the lowest frequency in the range and moving upward, sum the power distributed in each frequency until the result is
of the total power.
Determine the upper frequency value. Starting at the highest frequency in the range and moving downward, sum the power distributed in each frequency until the result reaches
of the total power.
The bandwidth between the lower and upper power frequency values is the occupied bandwidth.
The frequency halfway between the lower and upper frequency values is the center frequency.
The spectrum analyzer calculates Distortion Measurements using these steps.
Estimate spectral content by finding peaks in the spectrum. When the algorithm detects a peak, it records the width of the peak and clears all monotonically decreasing values by treating all these values as if they belong to the peak. Using this method, the algorithm removes all spectral content centered at DC (0 Hz) from the spectrum and records the amount of bandwidth cleared (W0).
Determine the fundamental power (P1) from the remaining maximum value of the displayed spectrum. Create a local estimate (Fe1) of the fundamental frequency by computing the central moment of the power near the peak. Record the bandwidth of the fundamental power content (W1). Then remove the power from the fundamental as in step 1.
Determine the power and width of the higher-order harmonics (P2, W2, P3, W3, etc.) in succession by examining the frequencies closest to the appropriate multiple of the local estimate (Fe1). Remove any spectral content that decreases monotonically about the harmonic frequency from the spectrum before proceeding to the next harmonic.
After removing the DC, fundamental, and harmonic content from the spectrum, examine the power of the remaining spectrum for its sum (Premaining), peak value (Pmaxspur), and median value (Pestnoise).
Compute the sum of all the removed bandwidth as Wsum = W0 + W1 + W2 +...+ Wn.
Compute the sum of powers of the second and higher-order harmonics as Pharmonic = P2 + P3 + P4 +...+ Pn.
Estimate the sum of the noise power as:
Where dF is the absolute difference between frequency bins, and RBW is the resolution bandwidth of the window.
Then compute the metrics for THD, THD%, SINAD, SNR, and SFDR from the estimates.
The harmonic distortion measurements use the spectrum trace shown in the display as the input to the measurements. The default
Hannwindow setting of the spectrum analyzer might exhibit leakage that can completely mask the noise floor of the measured signal.The harmonic measurements attempt to correct for leakage by ignoring all frequency content that decreases monotonically away from the maximum of harmonic peaks. If the window leakage covers more than 70% of the frequency bandwidth in your spectrum, you may see a blank reading (–) reported for SNR and SINAD. If your application can tolerate the increased equivalent noise bandwidth (ENBW), consider using a Kaiser window with a high attenuation (up to 330 dB) to minimize spectral leakage.
Ignore the DC component.
After windowing, the width of each harmonic component masks the noise power in the neighborhood of the fundamental frequency and harmonics. To estimate the noise power in each region, the spectrum analyzer computes the median noise level in the nonharmonic areas of the spectrum. It then extrapolates that value into each region.
Nth order intermodulation products occur at A*F1 + B*F2,
where F1 and F2 are the sinusoid input frequencies and |A| + |B| = N. A and B are integer values.
For intermodulation measurements, compute the third-order intercept (TOI) point as follows.
TOIlower = PF1 + (PF2 - P(2F1-F2))/2
TOIupper = PF2 + (PF1 - P(2F2-F1))/2
TOI = + (TOIlower + TOIupper)/2
Where P is power in decibels of the measured power referenced to 1 milliwatt (dBm).
The spectrum analyzer calculates the moving average using one of these methods:
Video bandwidth — The spectrum analyzer uses a time-domain lowpass filter to smooth the noise in the signal. The video bandwidth (VBW) filter smoothes the trace and decreases noise, and the spectrum analyzer applies the filter to the data before displaying it.
Video bandwidth is the bandwidth of the lowpass filter that spectrum analyzer uses to average or smooth the noise in the signal before displaying it in the scope. The spectrum analyzer computes the video bandwidth using this equation:
where,
Video bandwidth does not affect the level of the noise (noise floor), but only increases the signal-to-noise ratio and smoothes the trace of the noise. When you decrease the value of VBW, the signal-to-noise ratio improves.
The cutoff frequency of the video bandwidth filter is given by:
where Fs is the input sample rate and NFFT is the number of FFT points.
The spectrum analyzer shows the values of sample rate, VBW, and NFFT in the status bar at the bottom of the display. To enable, right-click the status bar and select
Sample Rate,VBW, andNFFT.Exponential — The moving average algorithm uses the exponential weighting method to update the weights and compute the moving average recursively for each Z vector that comes in by using the following recursive equations:
λ — Forgetting factor
— Weighting factor applied to the current Z vector
— Current Z vector
— Moving average until the previous Z vector
— Effect of the previous Z vectors on the average
— Moving average including the current Z vector
Running –– For each frame of the input, average the last Q scaled Z vectors, which are computed by the algorithm. The variable Q is the value you specify for the number of spectral averages. If the algorithm does not have enough Z vectors, the algorithm uses zeros to fill the empty elements.
Extended Capabilities
This block can be used for simulation visibility in systems that generate code, but is not included in the generated code.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic. See also Generate HDL Code with Annotations or Comments (HDL Coder) and Integrate Custom HDL Code by Using DocBlock (HDL Coder).
| Architecture | Description |
|---|---|
No HDL | Do not generate HDL code for this block. |
| PreserveUpstreamLogic | Control the removal of unconnected logic. The default
is |
This block can be used for simulation visibility in systems that generate PLC code, but is not included in the generated code.
Version History
Introduced in R2014bYou can now individually control the type of plot for each line. To control the type of plot for a line, select the line and set the Plot Type parameter accordingly.
You can now measure and plot the phase noise of a signal using the Spectrum Analyzer block.
To enable the phase noise measurements in the Spectrum Analyzer window, click the Measurements tab on the scope toolstrip and then click the Phase Noise button.
Note
To access the phase noise measurement settings, you must have a valid Mixed-Signal Blockset license.
The Spectrum Analyzer block now supports the running averaging
method to compute the power spectrum estimate. To enable this mode, set the
Averaging Method parameter in the
Estimation tab to Running and
the Spectral Averages parameter to a positive integer.
For more information, see the Algorithms section.
Previously, the Spectrum Analyzer block required a minimum number of samples to update the display for a given RBW value. Starting in R2024b, this limitation is removed. The scope now updates its display for any number of input samples and adjusts the RBW value accordingly.
The Spectrum Analyzer block can now automatically adjust the resolution bandwidth (RBW) so as to maintain the number of samples per spectral update at 1024 (Nsamples = 1024) irrespective of the window you select.
To enable this mode in the Spectrum Analyzer block, set:
Estimation Method to
Welch.Resolution Method to
RBW.RBW (Hz) to
Auto.
You can now increase the display precision to 15 digits using the Display Precision property in the scope settings under Display and Labels. This precision affects all the measurements and data that the scope displays on its status bar.
The Preserve colors for copy to clipboard property has been renamed to Preserve Colors and is now available in the scope toolstrip under Copy Display.
The Analyzer tab in spectrum analyzer has been renamed as Scope tab.
You can now specify the window length and FFT length in the spectrum analyzer under certain conditions. These parameters are available starting R2024a:
Resolution Method
Window Length
FFT Length
You can set Spectrum Unit to dBuV
when you set:
Input Domain to
Timeand Spectrum toRMS.Input Domain to
Frequency.
You can set Input Unit to dBuV
when you set Input Domain to
Frequency.
In R2023a, the Spectrum Analyzer block is more responsive and its
toolstrip interface is improved to provide you easy access to spectral analysis,
estimation, and measurements. You can configure and display Spectrum Analyzer
settings from the command line with the SpectrumAnalyzerBlockConfiguration object.
See Also
Objects
Functions
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)

