Variable FIR Decimation
Libraries:
DSP System Toolbox /
Filtering /
Multirate Filters
Description
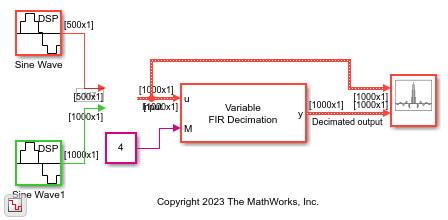
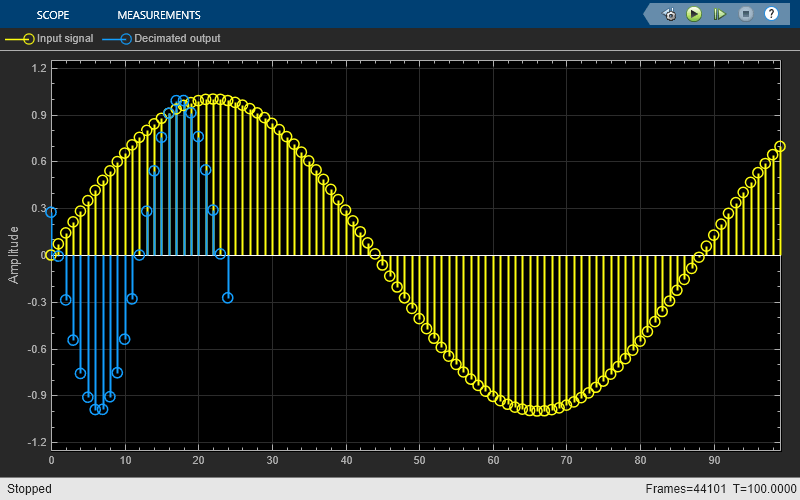
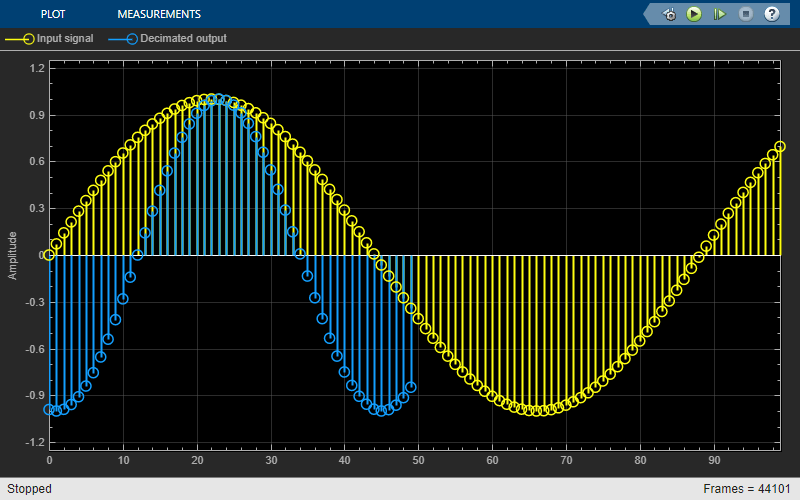
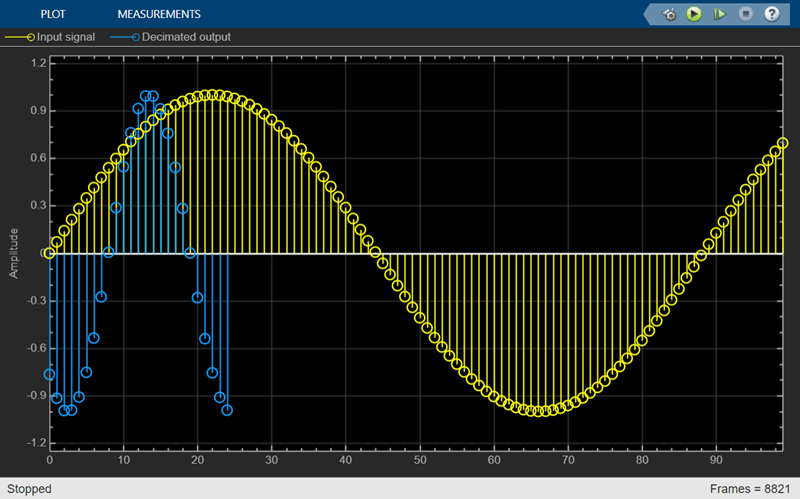
The Variable FIR Decimation block performs an efficient polyphase FIR decimation with a tunable decimation factor. You can update the decimation factor and the filter coefficients in the block dialog box or through an input port while the simulation is running. To control the decimation, you can specify the decimation factor or the output frame length.
When you specify the decimation factor, if the input frame length changes (variable-size signal) during simulation, the output frame length also changes in order to keep the decimation factor constant. When you specify the output frame length instead of the decimation factor, and if the input frame length changes (variable-size signal) during simulation, the decimation factor also changes in order to keep the output frame length constant.
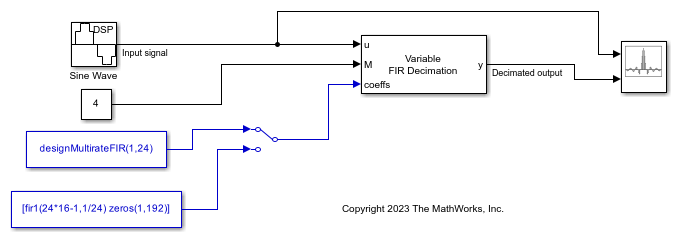
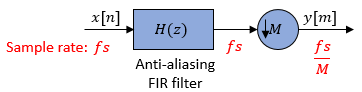
Conceptually, the FIR decimator (as shown in the schematic) consists of an anti-aliasing
FIR filter followed by a downsampler. To design an FIR anti-aliasing filter, use the designMultirateFIR function.
The FIR filter filters the data in each channel of the input using a direct-form FIR filter. The downsampler that follows downsamples each channel of filtered data by taking every M-th sample and discarding the M – 1 samples that follow. M is the value of the decimation factor. The resulting discrete-time signal has a sample rate that is 1/M times the original sample rate.
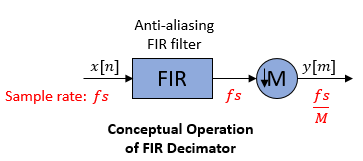
Note that the actual block algorithm implements a direct-form FIR polyphase structure, an efficient equivalent of the combined system depicted in the diagram. For more details, see Algorithms.
The block supports C and C++ code generation.
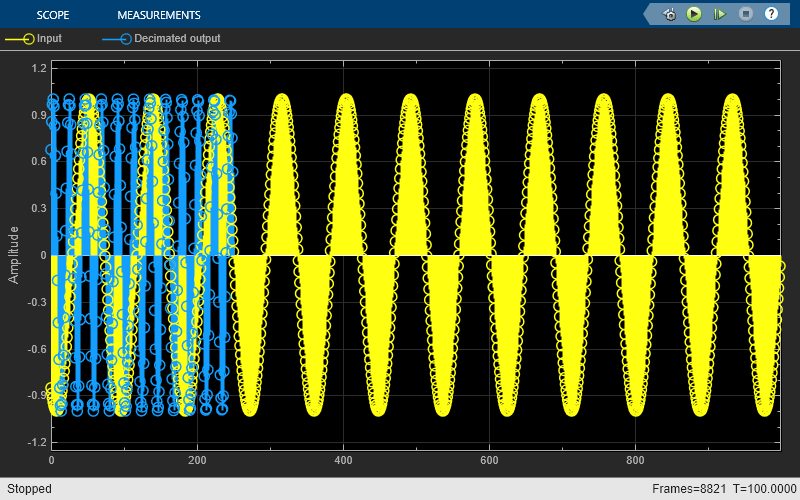
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Algorithms
The FIR decimation filter is implemented efficiently using a polyphase structure. For more information on polyphase filters, see Polyphase Subfilters.
To derive the polyphase structure, start with the transfer function of the FIR filter
where N+1 is the length of the FIR filter.
You can rearrange this equation as
where Mmax is the number of polyphase components, and its value equals the maximum decimation factor.
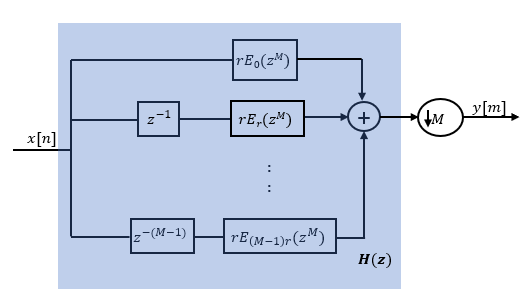
You can write H(z) as
where E0(zMmax), E1(zMmax), ..., EMmax-1(zMmax) are the polyphase components of the FIR filter H(z).
During simulation, the algorithm reconstructs the filter H(z) based on the current decimation factor M.
Rewriting H(z) in terms of the decimation factor M yields
where r = Mmax/M.
Conceptually, the FIR decimation filter contains a lowpass FIR filter followed by a downsampler.
Replace H(z) with its polyphase representation.
This is the multirate noble identity for decimation.
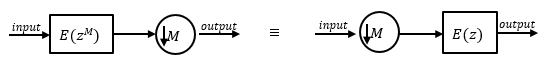
Applying the noble identity for decimation moves the downsampling operation to before the filtering operation. This move enables you to filter the signal at a lower rate.
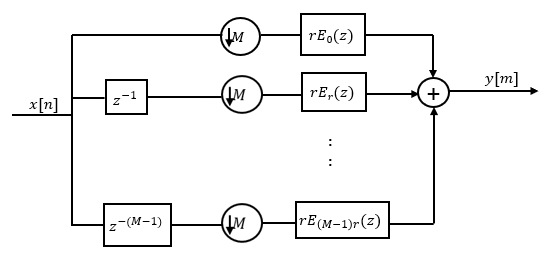
You can replace the delays and the decimation factor at the input with a commutator switch. The switch starts on the first branch 0 and moves in the counterclockwise direction as shown in this diagram. The accumulator at the output receives the processed input samples from each branch of the polyphase structure and accumulates these processed samples until the switch goes to branch 0. When the switch goes to branch 0, the accumulator outputs the accumulated value.
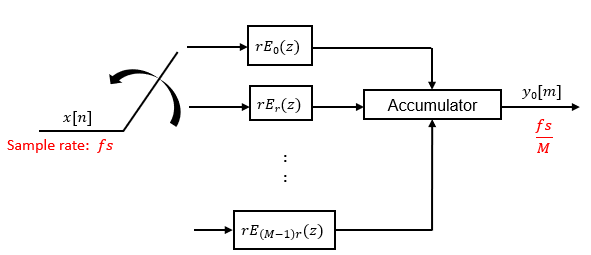
When the first input sample is delivered, the switch feeds this input to the branch 0 and the decimator computes the first output value. As more input samples come in, the switch moves in the counter clockwise direction through branches (M−1)r, (M−2)r, and all the way up to branch 0, delivering one sample at a time to each branch. When the switch comes to branch 0, the decimator outputs the next set of output values. This process continues as data keeps coming in. Every time the switch comes to the branch 0, the decimator outputs y[m]. The decimator effectively outputs one sample for every M samples it receives. Hence the sample rate at the output of the FIR decimation filter is fs/M.
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1996.