dsp.Channelizer
Polyphase FFT analysis filter bank
Description
The dsp.Channelizer
System object™ separates a broadband input signal into multiple narrow subbands using a fast
Fourier transform (FFT)-based analysis filter bank. The filter bank uses a prototype lowpass
filter and is implemented using a polyphase structure. You can specify the filter coefficients
directly or through design parameters.
To separate a broadband signal into multiple narrow subbands:
Create the
dsp.Channelizerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
channelizer = dsp.Channelizerdsp.ChannelSynthesizer
System object.
channelizer = dsp.Channelizer(M)NumFrequencyBands property set to M.
Example: channelizer = dsp.Channelizer(16)
channelizer = dsp.Channelizer(M,D)DecimationFactor property set to D.
Example: channelizer = dsp.Channelizer(16,8)
channelizer = dsp.Channelizer(Name=Value)DecimationFactor to 4.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Main Properties
Number of frequency bands M into which the object separates the input broadband signal, specified as a positive integer greater than 1. This property corresponds to the number of polyphase branches and the FFT length used in the filter bank.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Decimation factor D, specified as one of these:
"Number of frequency bands"–– When you change the value of theNumFrequencyBandsproperty, the decimation factor changes automatically. (since R2024a)Positive integer less than or equal to the number of frequency bands M.
If the decimation factor D equals the number of frequency bands M, then the M/D ratio equals 1, and the channelizer is known as the maximally decimated channelizer.
If the M/D ratio is greater than
1, the output sample rate is different from the channel spacing,
and the channelizer is known as the non-maximally decimated channelizer. If the ratio
is an integer, the channelizer is known as the integer-oversampled channelizer. If the
ratio is not an integer, say 4/3, the channelizer is known as the rationally
oversampled channelizer. For more details, see Algorithm.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Filter design parameters or filter coefficients, specified as one of these options:
"Number of taps per band and stopband attenuation"— Specify the filter design parameters through theNumTapsPerBandandStopbandAttenuationproperties."Coefficients"— Specify the filter coefficients directly using theLowpassCoefficientsproperty.
Number of filter coefficients each polyphase branch uses, specified as a positive
integer. The number of polyphase branches matches the number of frequency bands. The
total number of filter coefficients for the prototype lowpass filter is given by
NumFrequencyBands × NumTapsPerBand.
For a given stopband attenuation, increasing the number of taps per band narrows the
transition width of the filter. As a result, there is more usable bandwidth for each
frequency band at the expense of increased computation.
Dependencies
To enable this property, set Specification to
"Number of taps per band and stopband attenuation".
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Stopband attenuation of the lowpass filter, specified as a positive real scalar in dB. This value controls the maximum amount of aliasing from one frequency band to the next. When the stopband attenuation increases, the passband ripple decreases. For a given stopband attenuation, increasing the number of taps per band narrows the transition width of the filter. As a result, there is more usable bandwidth for each frequency band at the expense of increased computation.
Dependencies
To enable this property, set Specification to
"Number of taps per band and stopband attenuation".
Data Types: single | double
Coefficients of the prototype lowpass filter, specified as a row vector. The
default vector of coefficients is obtained using
rcosdesign(0.25,6,8,"sqrt"). There must be at least one
coefficient per frequency band. If the length of the lowpass filter is less than the
number of frequency bands, the object zero-pads the coefficients.
If you specify complex coefficients, the object designs a prototype filter that is centered at a nonzero frequency, also known as a bandpass filter. The modulated versions of the prototype bandpass filter appear with respect to the prototype filter and are wrapped around the frequency range [−Fs Fs]. For an example, see Channelizer with Complex Coefficients.
Tunable: Yes
Dependencies
To enable this property, set Specification to
"Coefficients".
Data Types: single | double
Complex Number Support: Yes
Code Generation Properties
Allow arbitrary frame length for fixed-size input signals in the generated code,
specified as true or false.
When you specify:
true–– The input frame length does not have to be a multiple of the decimation factor. The output of the object in the generated code is a variable-size array.false–– The input frame length must be a multiple of the decimation factor.
When you specify variable-size signals, the input frame length can be arbitrary and the object ignores this property in the generated code. When you run this object in MATLAB®, the object supports arbitrary input frame lengths for fixed-size and variable-size signals and this property does not affect the object behavior.
Data Types: logical
Usage
Description
Input Arguments
Data input, specified as an L-by-1 vector or an L-by-N matrix, with N > 1.
Under most conditions, the number of inputs rows L can be arbitrary and does not have to be a multiple of the number of frequency bands. See this table for details.
| Input Signal | When you Run Object in MATLAB | When you Generate Code Using MATLAB Coder™ |
|---|---|---|
| Fixed-size | Object supports arbitrary input frame length | Object supports arbitrary input frame length when you set
AllowArbitraryInputLength to true
while generating code |
| Variable-size | Object supports arbitrary input frame length | Object supports arbitrary input frame length |
Variable-size signals change in frame length once you lock the object while the fixed-size signals remain constant. When the object does not support arbitrary frame length, the input frame length must be a multiple of the number of frequency bands.
Data Types: single | double
Complex Number Support: Yes
Output Arguments
Channelizer output, returned as a matrix or a 3-D array.
If the input is an L-by-1 vector, then the output signal has an
upper bound size of
ceil(L/M)-by-M, where
M is the number of frequency bands. Each narrowband signal forms
a column in the output.
If the input has more than one channel, that is, it is of the form
L-by-N with N > 1, then the
output signal has an upper bound size of
ceil(L/M)-by-M-by-N.
Data Types: single | double
Complex Number Support: Yes
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
coeffs | Coefficients of prototype lowpass filter |
tf | Return transfer function of overall prototype lowpass filter |
polyphase | Return polyphase matrix |
freqz | Frequency response of filters in channelizer |
bandedgeFrequencies | Compute the band edge frequencies |
centerFrequencies | Compute center frequencies |
getFilters | Return matrix of channelizer FIR filters |
Examples
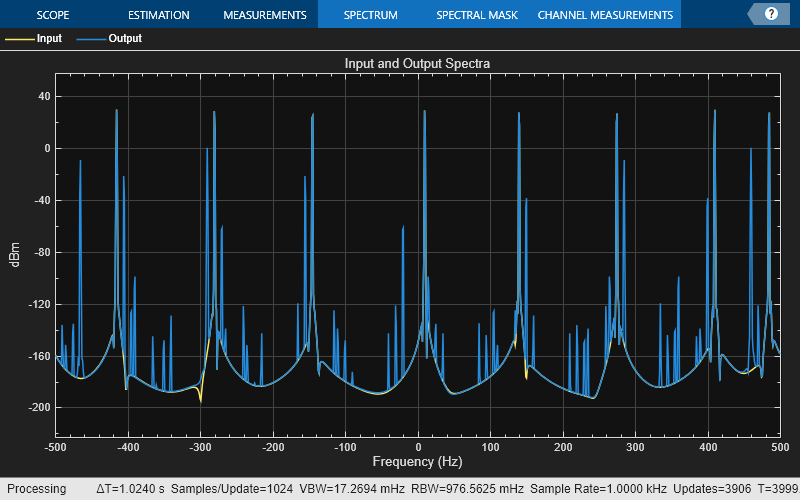
Channelize and synthesize a sine wave signal with multiple frequencies using an M -channel filter bank.
The M -channel filter bank contains an analysis filter bank section and a synthesis filter bank section. The dsp.Channelizer object implements the analysis filter bank section. The dsp.ChannelSynthesizer object implements the synthesis filter bank section. These objects use an efficient polyphase structure to implement the filter bank. For more details, see Polyphase Implementation under Algorithms on the object reference pages.
Initialization
Initialize the dsp.Channelizer and dsp.ChannelSynthesizer System objects. Each object is set up with 8 frequency bands, 8 polyphase branches in each filter, 12 coefficients per polyphase branch, and a stopband attenuation of 140 dB. Use a sine wave with multiple frequencies as the input signal. View the input spectrum and the output spectrum using a spectrum analyzer.
offsets = [-40,-30,-20,10,15,25,35,-15]; sinewave = dsp.SineWave(ComplexOutput=true,Frequency=offsets+(-375:125:500),... SamplesPerFrame=800); channelizer = dsp.Channelizer(StopbandAttenuation=140); synthesizer = dsp.ChannelSynthesizer(StopbandAttenuation=140); scope = spectrumAnalyzer(ShowLegend=true,... SampleRate=sinewave.SampleRate,... ChannelNames=["Input","Output"],... Title="Input and Output Spectra");
Streaming
Use the channelizer to split the broadband input signal into multiple narrow bands. Then pass the multiple narrowband signals into the synthesizer, which merges these signals to form the broadband signal. Compare the spectra of the input and output signals. The input and output spectra match very closely.
for i = 1:5000 x = sum(sinewave(),2); y = channelizer(x); v = synthesizer(y); scope(x,v) end
Create a dsp.Channelizer object and set the LowpassCoefficients property to a vector of complex coefficients.
Complex Coefficients
Using firpm, determine the coefficients of a Park-McClellan's optimal equiripple FIR filter of order 30, and frequency and amplitude characteristics described by F = [0 0.2 0.4 1.0] and A = [1 1 0 0] vectors, respectively.
Create a complex version of these coefficients by multiplying with a complex exponential. The resultant frequency response is that of a bandpass filter at the specified frequency, in this case 0.4.
blowpass = firpm(30,[0 .2 .4 1],[1 1 0 0]); N = length(blowpass)-1; Fc = 0.4; j = complex(0,1); bbandpass = blowpass.*exp(j*Fc*pi*(0:N));
Channelizer
Create a dsp.Channelizer object with 4 frequency bands and set the Specification property to 'Coefficients'.
chann = dsp.Channelizer(4,Specification="Coefficients");Pass the complex coefficients to the channelizer. The prototype filter is a bandpass filter with a center frequency of 0.4. The modulated versions of this filter appear with respect to the prototype filter and are wrapped around the frequency range [Fs Fs].
chann.LowpassCoefficients = bbandpass
chann =
dsp.Channelizer with properties:
Main
NumFrequencyBands: 4
DecimationFactor: 'Number of frequency bands'
Specification: 'Coefficients'
LowpassCoefficients: [0.0019 + 0.0000i 0.0005 + 0.0016i 0.0011 - 0.0008i 0.0051 + 0.0037i -0.0024 + 0.0073i -3.4175e-04 + 8.3704e-20i 0.0042 + 0.0128i -0.0174 + 0.0126i -0.0077 - 0.0056i -0.0070 + 0.0214i -0.0514 + 0.0000i … ] (1×31 double)
Show all properties
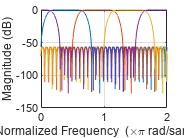
Visualize the frequency response of the channelizer.
freqz(chann)
More About
The generic analysis filter bank consists of a series of parallel bandpass filters that split an input broadband signal, x[n], into a series of narrow subbands. Each bandpass filter retains a different portion of the input signal. After the bandwidth is reduced by one of the bandpass filters, the signal is downsampled to a lower sampling rate commensurate with the new bandwidth.

To implement the analysis filter bank efficiently, the channelizer uses a prototype lowpass filter.
The prototype lowpass filter has an impulse response of h[n], a normalized two-sided bandwidth of 2π/M, and a cutoff frequency of π/M. M is the number of frequency bands, that is, the branches of the analysis filter bank. This value corresponds to the FFT length that the filter bank uses. M can be high on the order of 2048 or more. The stopband attenuation determines the minimum level of interference (aliasing) from one frequency band to another. The passband ripple must be small so that the input signal is not distorted in the passband.
The prototype lowpass filter corresponds to H0(z) in the filter bank. The first branch of the filter bank contains H0(z) followed by the decimator. The other M – 1 branches contain filters that are modulated versions of the prototype filter. The modulation factor is given by the following equation:
The transfer function of the modulated kth bandpass filter is given by:
This figure shows the frequency response of M filters.

To obtain the frequency response characteristics of the filter Hk(z), where k = 1, … , M−1, uniformly shift the frequency response of the prototype filter, H0(z), by multiples of 2π/M. Each subband filter, Hk(z), {k = 1, … , M – 1}, is derived from the prototype filter.
Following is an equivalent representation of the frequency response diagram with ω ranging from [−π π].

The frequency components in the input signal, x[n], are translated in frequency to baseband by multiplying x[n] with the complex exponentials, , where , and . The resulting product signals are passed through the lowpass filters, H0(z). The output of the lowpass filter is relatively narrow in bandwidth. Downsample the signal commensurate with the new bandwidth. Choose a decimation factor, D ≤ M, where M is the number of branches of the analysis filter bank. When D < M, the channelizer is known as oversampled or non-maximally decimated channelizer.
The figure shows an analysis filter bank that uses the prototype lowpass filter.

y1[m], y2[m], … , yM−1[m] are narrow subband signals translated into baseband.
Algorithms
The analysis filter bank can be implemented efficiently using the polyphase structure. For more details on the analysis filter bank, see Analysis Filter Bank.
To derive the polyphase structure, start with the transfer function of the prototype lowpass filter:
N + 1 is the length of the prototype filter.
You can rearrange this equation as follows:
M is the number of polyphase components.
You can write this equation as:
E0(zM), E1(zM), … , EM−1(zM) are polyphase components of the prototype lowpass filter H0(z).
The other filters in the filter bank, Hk(z), where k = 1, … , M−1, are modulated versions of this prototype filter.
You can write the transfer function of the kth modulated bandpass filter as .
Replacing z with ze-jwk and ,
In polyphase form, the equation is as follows:
For all M channels in the filter bank, the transfer function H(z) is given by:
When D = M, the channelizer is known as the maximally decimated channelizer or critically sampled channelizer.
Here is the multirate noble identity for decimation, assuming that D = M.
![]()
For example, consider the first branch of the filter bank that contains the lowpass filter.
![]()
Replace H0(z) with its polyphase representation.

After applying the noble identity for decimation, you can replace the delays and the decimation factor with a commutator switch. The switch starts on the first branch 0 and moves in the counterclockwise direction as shown in the following diagram. The accumulator at the output receives the processed input samples from each branch of the polyphase structure and accumulates these processed samples until the switch goes to branch 0. When the switch goes to branch 0, the accumulator outputs the accumulated value.

For all M channels in the filter bank, the transfer function H(z) is given by:
The matrix on the left is an inverse discrete Fourier transform (IDFT) matrix. With the IDFT matrix, the efficient implementation of the lowpass prototype-based filter bank looks like the following.
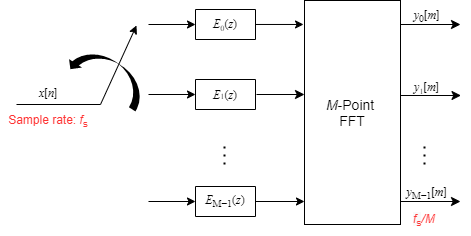
When the channelizer receives the first input sample, the switch feeds this input to the branch 0 and the channelizer computes the first set of output values. As more input samples come in, the switch moves in the counterclockwise direction through branches M−1, M−2, all the way up to branch 0, delivering one sample at a time to each branch. When the switch comes to branch 0, the channelizer outputs the next set of output values. This process continues as the data keeps coming in. Every time the switch comes to the first branch 0, the channelizer outputs y0[m], y1[m], … , yM-1[m]. Each branch in the channelizer effectively outputs one sample for every M samples it receives. Hence, the sample rate at the output of the channelizer is fs/M.
If you use the M-point FFT, the implementation looks like the following.
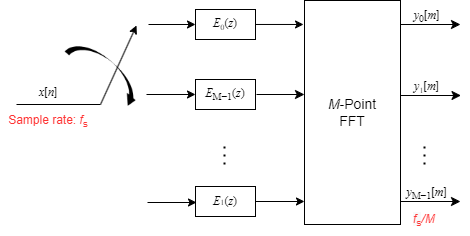
When the switch delivers the first sample to branch 0, the channelizer computes the first set of output values. As more data comes in, the switch moves in the clockwise direction to branches M−1, M−2, all the way up to branch 1, delivering one sample at a time to each branch. When the switch comes to branch 0, the channelizer outputs the next set of output values. This process continues as more data keeps coming in.
When D < M, the channelizer is known as the non-maximally decimated channelizer or oversampled channelizer. In this configuration, the output sample rate is different from the channel spacing. The non-maximally decimated channelizers offer increased design freedom, but at the expense of increasing computational cost.
If the ratio M/D equals an integer that is greater than 1 and is less than or equal to M−1, the channelizer is known as integer-oversampled channelizer. If the ratio M/D is not an integer, then the channelizer is known as rationally-oversampled channelizer.
In this configuration, when the first input sample is delivered, the switch feeds this input to branch 0 and the channelizer computes the first set of output values. As more input samples come in, the switch moves in the counterclockwise direction through branches D−1, D−2, all the way up to branch 0, delivering one sample at a time to each branch. When the switch comes to branch 0, the channelizer outputs the next set of output values. This process continues as the data keeps coming in. Every time the switch comes to the first branch 0, the channelizer outputs y0[m], y1[m], … , yM-1[m].
As more data keeps coming in and the switch feeds these samples to the first D addresses, the formal contents of these addresses are shifted to the next set of D addresses, and this process of data shift continues every time there is a new set of D input samples.
For every D input samples that are fed to the polyphase structure, the channelizer outputs M samples, y0[m], y1[m], … , yM-1[m]. This process increases the output sample rate from fs/M in the case of a maximally decimated channelizer, to fs/D in the case of a non-maximally decimated channelizer.
For more details, see [2].
After each D-point data sequence is delivered to the partitioned M-stage polyphase filter, the outputs of the M stages are computed and conditioned for delivery to the M-point FFT. The data shifting through the filter introduces frequency-dependent phase shift. To correct for this phase shift and alias all bands to DC, a circular shift buffer is inserted after the polyphase filters and before the M-point FFT.
With the commutator switch followed by M-stage polyphase filter, circular shift buffer, and a DFT matrix, the efficient implementation of the lowpass prototype-based filter bank looks like this.

References
[1] Harris, Fredric J, Multirate Signal Processing for Communication Systems, Prentice Hall PTR, 2004.
[2] Harris, F.J., Chris Dick, and Michael Rice. "Digital Receivers and Transmitters Using Polyphase Filter Banks for Wireless Communications." IEEE® Transactions on Microwave Theory and Techniques. 51, no. 4 (2003).
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2016bYou can now set the DecimationFactor property to
NumFrequencyBands. When you change the value of the
NumFrequencyBands property, the decimation factor changes
automatically.
Existing MATLAB scripts using the dsp.Channelizer object continue to run in
R2024a.
Starting in R2022b, this object supports an input signal with an arbitrary frame length, so the input frame length does not have to be a multiple of the number of frequency bands.
When you generate code, to support arbitrary frame length for fixed-size signals, you
must set the AllowArbitraryInputLength property to
true while generating code.
See Also
Functions
coeffs|tf|polyphase|freqz|bandedgeFrequencies|centerFrequencies|getFilters
Objects
dsp.ChannelSynthesizer|dsp.FIRHalfbandDecimator|dsp.FIRHalfbandInterpolator|dsp.IIRHalfbandDecimator|dsp.DyadicAnalysisFilterBank
Blocks
- Channelizer | Channel Synthesizer | Dyadic Analysis Filter Bank | Two-Channel Analysis Subband Filter
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)