mle

Maximum likelihood estimates

Syntax

phat = mle(data)

phat = mle(data,Name,Value)

[phat,pci] = mle(___)

Description

phat = mle(data) returns maximum likelihood estimates (MLEs) for the parameters of a normal distribution, using the sample data data.

phat = mle(data,Name,Value) specifies options using one or more name-value arguments.

For example, you can specify the distribution type by using one of these name-value arguments: Distribution, pdf, logpdf, or nloglf.

• To compute MLEs for a built-in distribution, specify the distribution type by using Distribution. For example, 'Distribution','Beta' specifies to compute the MLEs for the beta distribution.

• To compute MLEs for a custom distribution, define the distribution by using pdf, logpdf, or nloglf, and specify the initial parameter values by using Start.

[phat,pci] = mle(___) also returns the confidence intervals for the parameters using any of the input argument combinations in the previous syntaxes.

Examples

Find MLEs for Built-in Distribution

Find MLEs for a built-in distribution that you specify using the Distribution name-value argument.

Load the sample data.

load carbig

The variable MPG contains the miles per gallon for different models of cars.

Draw a histogram of the MPG data.

 histogram(MPG)

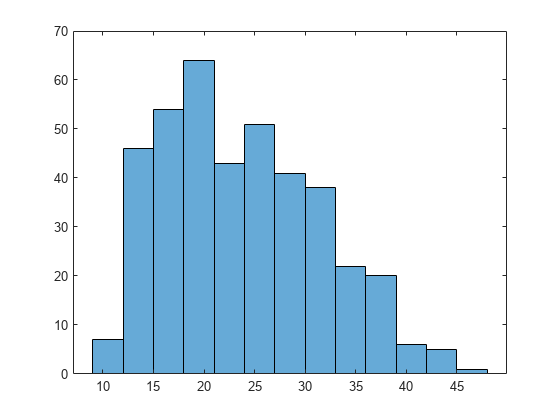
The distribution is somewhat right skewed. A symmetric distribution, such as a normal distribution, might not be a good fit.

Estimate the parameters of the Burr Type XII distribution for the MPG data.

phat = mle(MPG,'Distribution','burr')

phat = 1×3

   34.6447    3.7898    3.5722

The MLE for the scale parameter α is 34.6447. The estimates for the two shape parameters $$c$$ and $$k$$ of the Burr Type XII distribution are 3.7898 and 3.5722, respectively.

Compute MLE and Confidence Interval

Generate 100 random observations from a binomial distribution with the number of trials $$n$$ = 20 and the probability of success $$p$$ = 0.75.

rng('default') % For reproducibility
data = binornd(20,0.75,100,1);

Estimate the probability of success and 99% confidence limits using the simulated sample data. You must specify the number of trials (NTrials) for the binomial distribution.

[phat,pci] = mle(data,'Distribution','binomial','NTrials',20, ...
    'Alpha',.01)

phat = 0.7615

pci = 2×1

    0.7361
    0.7856

The estimate of the probability of success is 0.7615, and the lower and upper limits of the 99% confidence interval are 0.7361 and 0.7856, respectively. This interval covers the true value used to simulate the data.

Fit Custom Probability Density Function (pdf)

Generate sample data of size 1000 from a noncentral chi-square distribution with degrees of freedom 8 and noncentrality parameter 3.

rng default % for reproducibility
x = ncx2rnd(8,3,1000,1);

Estimate the parameters of the noncentral chi-square distribution from the sample data. The Distribution name-value argument does not support the noncentral chi-square distribution. Therefore, you need to define a custom noncentral chi-square pdf using the pdf name-value argument and the ncx2pdf function. You must also specify the initial parameter values (Start name-value argument) for the custom distribution.

[phat,pci] = mle(x,'pdf',@(x,v,d)ncx2pdf(x,v,d),'Start',[1,1])

phat = 1×2

    8.1052    2.6693

pci = 2×2

    7.1120    1.6025
    9.0983    3.7362

The estimate for the degrees of freedom is 8.1052 and the noncentrality parameter is 2.6693. The 95% confidence interval for the degrees of freedom is (7.1120,9.0983), and the interval for the noncentrality parameter is (1.6025,3.7362). The confidence intervals include the true parameter values of 8 and 3, respectively.

Fit Custom Log Probability Density Function (pdf)

Load the sample data.

load('readmissiontimes.mat');

The data includes ReadmissionTime, which has readmission times for 100 patients. This data is simulated.

Define a custom log pdf for a Weibull distribution with the scale parameter lambda and the shape parameter k.

custlogpdf = @(data,lambda,k) ...
    log(k) - k*log(lambda) + (k-1)*log(data) - (data/lambda).^k;

Estimate the parameters of the custom distribution and specify its initial parameter values (Start name-value argument).

phat = mle(ReadmissionTime,'logpdf',custlogpdf,'Start',[1,0.75])

phat = 1×2

    7.5727    1.4540

The scale and shape parameters of the custom distribution are 7.5727 and 1.4540, respectively.

Fit Custom Negative Loglikelihood Function

Load the sample data.

load('readmissiontimes.mat')

The data includes ReadmissionTime, which has readmission times for 100 patients. This data is simulated.

Define a custom negative loglikelihood function for a Poisson distribution with the parameter lambda, where 1/lambda is the mean of the distribution. You must define the function to accept a logical vector of censorship information and an integer vector of data frequencies, even if you do not use these values in the custom function.

custnloglf = @(lambda,data,cens,freq) ...
    - length(data)*log(lambda) + sum(lambda*data,'omitnan');

Estimate the parameter of the custom distribution and specify its initial parameter value (Start name-value argument).

phat = mle(ReadmissionTime,'nloglf',custnloglf,'Start',0.05)

phat = 0.1462

Fit Distribution with Known Parameter

Generate sample data of size 1000 from a noncentral chi-square distribution with degrees of freedom 10 and noncentrality parameter 5.

rng('default') % For reproducibility
x = ncx2rnd(10,5,1000,1);

Suppose the noncentrality parameter is fixed at the value 5. Estimate the degrees of freedom of the noncentral chi-square distribution from the sample data. To do this, define a custom noncentral chi-square pdf using the pdf name-value argument.

[phat,pci] = mle(x,'pdf',@(x,v)ncx2pdf(x,v,5),'Start',1)

phat = 9.9307

pci = 2×1

    9.5626
   10.2989

The estimate for the noncentrality parameter is 9.9307, and the lower and upper limits of the 95% confidence interval are 9.5626 and 10.2989. The confidence interval includes the true parameter value of 10.

Fit Distribution with Additional Parameter

Add a scale parameter to the chi-square distribution for adapting to the scale of data, and fit the distribution.

Generate sample data of size 1000 from a chi-square distribution with degrees of freedom 5, and scale the data by a factor of 100.

rng default % For reproducibility
x = 100*chi2rnd(5,1000,1);

Estimate the degrees of freedom and the scaling factor. To do this, define a custom chi-square probability density function using the pdf name-value argument. The density function requires a $$1/s$$ factor for data scaled by $$s$$.

[phat,pci] = mle(x,'pdf',@(x,v,s)chi2pdf(x/s,v)/s,'Start',[1,200])

phat = 1×2

    5.1079   99.1681

pci = 2×2

    4.6862   90.1215
    5.5297  108.2146

The estimate for the degrees of freedom is 5.1079 and the scale is 99.1681. The 95% confidence interval for the degrees of freedom is (4.6862,5.5279), and the interval for the scale parameter is (90.1215,108.2146). The confidence intervals include the true parameter values of 5 and 100, respectively.

Fit Custom Distribution to Right-Censored Data

Load the sample data.

load('readmissiontimes.mat');

The data includes ReadmissionTime, which has readmission times for 100 patients. The column vector Censored contains the censorship information for each patient, where 1 indicates a right-censored observation, and 0 indicates that the exact readmission time is observed. This data is simulated.

Define a custom probability density function (pdf) and a cumulative distribution function (cdf) for an exponential distribution with the parameter lambda, where 1/lambda is the mean of the distribution. To fit the distribution to a censored data set, you must pass both the pdf and cdf to the mle function.

custpdf = @(data,lambda) lambda*exp(-lambda*data);
custcdf = @(data,lambda) 1-exp(-lambda*data);

Estimate the parameter lambda of the custom distribution for the censored sample data. Specify the initial parameter value (Start name-value argument) for the custom distribution.

phat = mle(ReadmissionTime,'pdf',custpdf,'cdf',custcdf, ...
    'Start',0.05,'Censoring',Censored)

phat = 0.1096

Find MLEs for Double-Censored Data

Generate double-censored survival data and find the MLEs for a built-in distribution of the data. Then, use the MLEs to create a probability distribution object.

Generate failure times from a Birnbaum-Saunders distribution.

rng('default')  % For reproducibility
failuretime = random('BirnbaumSaunders',0.3,1,[100,1]);

Assume that the study starts at time 0.1 and ends at time 0.9. The assumption implies that failure times less than 0.1 are left censored, and failure times greater than 0.9 are right censored.

Create a vector in which each element indicates the censorship status of the corresponding observation in failuretime. Use –1, 1, and 0 to indicate left-censored, right-censored, and fully observed observations, respectively.

L = 0.1;
U = 0.9;
left_censored = (failuretime<L);
right_censored = (failuretime>U);
c = right_censored - left_censored;

Find MLEs for the double-censored data. Specify the censorship information by using the Censoring name-value argument.

phat = mle(failuretime,'Distribution','BirnbaumSaunders','Censoring',c)

phat = 1×2

    0.2632    1.3040

Create a probability distribution object with the MLEs by using the makedist function.

pd = makedist('BirnbaumSaunders','beta',phat(1),'gamma',phat(2))

pd = 
  BirnbaumSaundersDistribution

  Birnbaum-Saunders distribution
     beta = 0.263184
    gamma =    1.304

pd is a BirnbaumSaundersDistribution object. You can use the object functions of pd to evaluate the distribution and generate random numbers. Display the supported object functions.

methods(pd)

Methods for class prob.BirnbaumSaundersDistribution:

cdf        iqr        negloglik  plot       std        
gather     mean       paramci    proflik    truncate   
icdf       median     pdf        random     var        

For example, compute the mean and the variance of the distribution by using the mean and var functions, respectively.

mean(pd)

ans = 0.4869

var(pd)

ans = 0.3681

Find MLEs for Interval-Censored Data

Generate sample data that represents machine failure times following the Weibull distribution.

rng('default') % For reproducibility
failureTimes = wblrnd(5,2,[200,1]);

Specify that observed failure times are values rounded to the nearest second.

observed = round(failureTimes);

observed is interval-censored data. An observation t in observed indicates that the event occurred after time t–0.5 and before time t+0.5.

Create a two-column matrix that includes the censorship information.

intervalTimes = [observed-0.5 observed+0.5];

The failure time must be positive. Find values smaller than eps, and change them to eps.

intervalTimes(intervalTimes < eps) = eps;

Find the MLEs for the Weibull distribution parameters by using intervalTimes.

params = mle(intervalTimes,'Distribution','Weibull')

params = 1×2

    5.0067    2.0049

Plot the results.

figure
histogram(observed,'Normalization','pdf')
hold on
x = linspace(0,max(observed));
plot(x,wblpdf(x,params(1),params(2)))
legend('Observed Samples','Fitted Distribution')
hold off

Find MLEs for Distribution with Finite Support

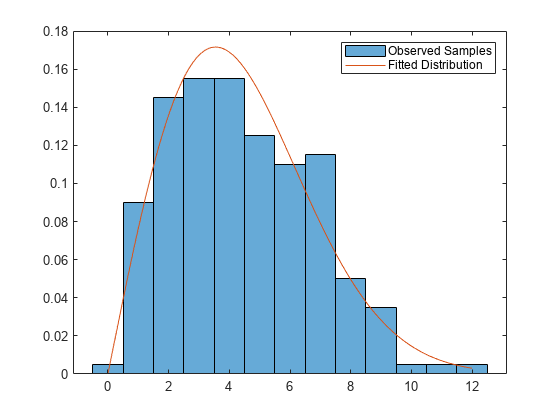
Generate samples from a distribution with finite support, and find the MLEs with customized options for the iterative estimation process.

For a distribution with a region that has zero probability density, mle might try some parameters that have zero density, causing the function to fail to find MLEs. To avoid this problem, you can turn off the option that checks for invalid function values and specify the parameter bounds when you call the mle function.

Generate sample data of size 1000 from a Weibull distribution with the scale parameter 1 and shape parameter 1. Shift the samples by adding 10.

rng('default') % For reproducibility
data = wblrnd(1,1,[1000,1]) + 10;
histogram(data,'Normalization','pdf')

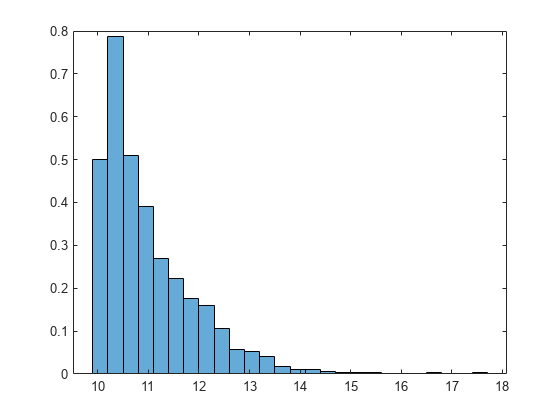
The histogram shows no samples smaller than 10, indicating that the distribution has zero probability in the region smaller than 10. This distribution is a three-parameter Weibull distribution, which includes a third parameter for location (see Three-Parameter Weibull Distribution).

Define a probability density function (pdf) for the three-parameter Weibull distribution.

custompdf = @(x,a,b,c) wblpdf(x-c,a,b);

Find the MLEs by using the mle function. Specify the Options name-value argument to turn off the option that checks for invalid function values. Also, specify the parameter bounds by using the LowerBound and UpperBound name-value arguments. The scale and shape parameters must be positive, and the location parameter must be smaller than the minimum of the sample data.

params = mle(data,'pdf',custompdf,'Start',[5 5 5], ...
     'Options',statset('FunValCheck','off'), ...
     'LowerBound',[0 0 -Inf],'UpperBound',[Inf Inf min(data)])

params = 1×3

    1.0258    1.0618   10.0004

The mle function finds accurate estimates for the three parameters. For more details on specifying custom options for the iterative process, see the example Three-Parameter Weibull Distribution.

Input Arguments

data — Sample data and censorship information

vector | two-column matrix

Sample data and censorship information, specified as a vector of sample data or a two-column matrix of sample data and censorship information.

You can specify the censorship information for the sample data by using either the data argument or the Censoring name-value argument. mle ignores the Censoring argument value if data is a two-column matrix.

Specify data as a vector or a two-column matrix depending on the censorship types of the observations in data.

• Fully observed data — Specify data as a vector of sample data.

• Data that contains fully observed, left-censored, or right-censored observations — Specify data as a vector of sample data, and specify the Censoring name-value argument as a vector that contains the censorship information for each observation. The Censoring vector can contain 0, –1, and 1, which refer to fully observed, left-censored, and right-censored observations, respectively.

• Data that includes interval-censored observations — Specify data as a two-column matrix of sample data and censorship information. Each row of data specifies the range of possible survival or failure times for each observation, and can have one of these values:

  • [t,t] — Fully observed at t

  • [–Inf,t] — Left-censored at t

  • [t,Inf] — Right-censored at t

  • [t1,t2] — Interval-censored between [t1,t2], where t1 < t2

  For the list of built-in distributions that support censored observations, see Censoring.

  mle ignores NaN values in data. Additionally, any NaN values in the censoring vector (Censoring) or frequency vector (Frequency) cause mle to ignore the corresponding rows in data.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Censoring',Cens,'Alpha',0.01,'Options',Opt instructs mle to estimate the parameters for the distribution of censored data specified by the array Cens, compute the 99% confidence limits for the parameter estimates, and use the algorithm control parameters specified by the structure Opt.

Options to Specify Built-in Distribution

Distribution — Distribution type

'normal' (default) | character vector or string scalar of distribution type

Distribution type for which to estimate parameters, specified as one of the values in this table.

Distribution Value	Distribution Type	First Parameter	Second Parameter	Third Parameter	Fourth Parameter
'Bernoulli'	Bernoulli Distribution	p: probability of success for each trial	N/A	N/A	N/A
'Beta'	Beta Distribution	a: first shape parameter	b: second shape parameter	N/A	N/A
'Binomial'	Binomial Distribution	p: probability of success for each trial	N/A	N/A	N/A
'BirnbaumSaunders'	Birnbaum-Saunders Distribution	β: scale parameter	γ: shape parameter	N/A	N/A
'Burr'	Burr Type XII Distribution	α: scale parameter	c: first shape parameter	k: second shape parameter	N/A
'Discrete Uniform' or 'unid'	Uniform Distribution (Discrete)	n: maximum observable value	N/A	N/A	N/A
'Exponential'	Exponential Distribution	μ: mean	N/A	N/A	N/A
'Extreme Value' or 'ev'	Extreme Value Distribution	μ: location parameter	σ: scale parameter	N/A	N/A
'Gamma'	Gamma Distribution	a: shape parameter	b: scale parameter	N/A	N/A
'Generalized Extreme Value' or 'gev'	Generalized Extreme Value Distribution	k: shape parameter	σ: scale parameter	μ: location parameter	N/A
'Generalized Pareto' or 'gp'	Generalized Pareto Distribution	k: tail index (shape) parameter	σ: scale parameter	N/A	N/A
'Geometric'	Geometric Distribution	p: probability parameter	N/A	N/A	N/A
'Half Normal' or 'hn'	Half-Normal Distribution	σ: scale parameter	N/A	N/A	N/A
'InverseGaussian'	Inverse Gaussian Distribution	μ: scale parameter	λ: shape parameter	N/A	N/A
'Logistic'	Logistic Distribution	μ: mean	σ: scale parameter	N/A	N/A
'LogLogistic'	Loglogistic Distribution	μ: mean of logarithmic values	σ: scale parameter of logarithmic values	N/A	N/A
'LogNormal'	Lognormal Distribution	μ: mean of logarithmic values	σ: standard deviation of logarithmic values	N/A	N/A
'Nakagami'	Nakagami Distribution	μ: shape parameter	ω: scale parameter	N/A	N/A
'Negative Binomial' or 'nbin'	Negative Binomial Distribution	r: number of successes	p: probability of success in a single trial	N/A	N/A
'Normal'	Normal Distribution	μ: mean	σ: standard deviation	N/A	N/A
'Poisson'	Poisson Distribution	λ: mean	N/A	N/A	N/A
'Rayleigh'	Rayleigh Distribution	b: scale parameter	N/A	N/A	N/A
'Rician'	Rician Distribution	s: noncentrality parameter	σ: scale parameter	N/A	N/A
'Stable'	Stable Distribution	α: first shape parameter	β: second shape parameter	γ: scale parameter	δ: location parameter
'tLocationScale'	t Location-Scale Distribution	μ: location parameter	σ: scale parameter	ν: shape parameter	N/A
'Uniform'	Uniform Distribution (Continuous)	a: lower endpoint (minimum)	b: upper endpoint (maximum)	N/A	N/A
'Weibull' or 'wbl'	Weibull Distribution	a: scale parameter	b: shape parameter	N/A	N/A

mle does not estimate these distribution parameters:

• Number of trials for the binomial distribution. Specify the parameter by using the NTrials name-value argument.

• Location parameter of the half-normal distribution. Specify the parameter by using the mu name-value argument.

• Location parameter of the generalized Pareto distribution. Specify the parameter by using the theta name-value argument.

If the sample data is truncated or includes left-censored or interval-censored observations, you must specify the Start name-value argument for the Burr distribution and the stable distribution.

Example: 'Distribution','Rician'

NTrials — Number of trials for binomial distribution

scalar | vector

Number of trials for the corresponding element of data for the binomial distribution, specified as a scalar or a vector with the same number of rows as data.

This argument is required when Distribution is 'Binomial' (binomial distribution).

Example: 'Ntrials',10

Data Types: single | double

theta — Location (threshold) parameter for generalized Pareto distribution

scalar

Location (threshold) parameter for the generalized Pareto distribution, specified as a scalar.

This argument is valid only when Distribution is 'Generalized Pareto' (generalized Pareto distribution).

The default value is 0 when the sample data data includes only nonnegative values. You must specify theta if data includes negative values.

Example: 'theta',1

Data Types: single | double

mu — Location parameter for half-normal distribution

scalar

Location parameter for the half-normal distribution, specified as a scalar.

This argument is valid only when Distribution is 'Half Normal' (half-normal distribution).

The default value is 0 when the sample data data includes only nonnegative values. You must specify mu if data includes negative values.

Example: 'mu',1

Data Types: single | double

Options to Define Custom Distribution

pdf — Custom probability density function

function handle | cell array

Custom probability distribution function (pdf), specified as a function handle or a cell array containing a function handle and additional arguments to the function.

The custom function accepts a vector containing sample data, one or more individual distribution parameters, and any additional arguments passed by a cell array as input parameters. The function returns a vector of probability density values.

Example: 'pdf',@newpdf

Data Types: function_handle | cell

cdf — Custom cumulative distribution function

function handle | cell array

Custom cumulative distribution function (cdf), specified as a function handle or a cell array containing a function handle and additional arguments to the function.

The custom function accepts a vector containing sample data, one or more individual distribution parameters, and any additional arguments passed by a cell array as input parameters. The function returns a vector of cdf values.

To compute MLEs for censored or truncated observations, you must define both cdf and pdf. For fully observed and untruncated observations, mle does not use cdf. You can specify the censorship information by using either data or Censoring and specify the truncation bounds by using TruncationBounds.

Example: 'cdf',@newcdf

Data Types: function_handle | cell

logpdf — Custom log probability density function

function handle | cell array

Custom log probability density function, specified as a function handle or a cell array containing a function handle and additional arguments to the function.

The custom function accepts a vector containing sample data, one or more individual distribution parameters, and any additional arguments passed by a cell array as input parameters. The function returns a vector of log probability values.

Example: 'logpdf',@customlogpdf

Data Types: function_handle | cell

logsf — Custom log survival function

function handle | cell array

Custom log survival function, specified as a function handle or a cell array containing a function handle and additional arguments to the function.

The custom function accepts a vector containing sample data, one or more individual distribution parameters, and any additional arguments passed by a cell array as input parameters. The function returns a vector of log survival probability values.

To compute MLEs for censored or truncated observations, you must define both logsf and logpdf. For fully observed and untruncated observations, mle does not use logsf. You can specify the censorship information by using either data or Censoring and specify the truncation bounds by using TruncationBounds.

Example: 'logsf',@logsurvival

Data Types: function_handle | cell

nloglf — Custom negative loglikelihood function

function handle | cell array

Custom negative loglikelihood function, specified as a function handle or a cell array containing a function handle and additional arguments to the function.

The custom function accepts the following input arguments, in the order listed in the table.

Input Argument of Custom Function	Description
params	Vector of distribution parameter values. mle detects the number of parameters from the number of elements in Start.
data	Sample data. The data value is a vector of sample data or a two-column matrix of sample data and censorship information.
cens	Logical vector of censorship information. nloglf must accept cens even if you do not use the Censoring name-value argument. In this case, you can write nloglf to ignore cens.
freq	Integer vector of data frequencies. nloglf must accept freq even if you do not use the Frequency name-value argument. In this case, you can write nloglf to ignore freq.
trunc	Two-element numeric vector of truncation bounds. nloglf must accept trunc if you use the TruncationBounds name-value argument.

nloglf can optionally accept the additional arguments passed by a cell array as input parameters.

nloglf returns a scalar negative loglikelihood value and, optionally, a negative loglikelihood gradient vector (see the GradObj field in the Options name-value argument).

Example: 'nloglf',@negloglik

Data Types: function_handle | cell

Other Options

Censoring — Indicator of censored data

vector of 0s (default) | vector consisting of 0, –1, and 1

Indicator of censored data, specified as a vector consisting of 0, –1, and 1, which indicate fully observed, left-censored, and right-censored observations, respectively. Each element of the Censoring value indicates the censorship status of the corresponding observation in data. The Censoring value must have the same size as data. The default is a vector of 0s, indicating all observations are fully observed.

You cannot specify interval-censored observations using this argument. If the sample data includes interval-censored observations, specify data using a two-column matrix. mle ignores the Censoring value if data is a two-column matrix.

mle supports censoring for the following built-in distributions and a custom distribution.

Distribution Value	Distribution Type
'BirnbaumSaunders'	Birnbaum-Saunders
'Burr'	Burr Type XII
'Exponential'	Exponential
'Extreme Value' or 'ev'	Extreme value
'Gamma'	Gamma
'InverseGaussian'	Inverse Gaussian
'Logistic'	Logistic
'LogLogistic'	Loglogistic
'LogNormal'	Lognormal
'Nakagami'	Nakagami
'Normal'	Normal
'Rician'	Rician
'tLocationScale'	t location-scale
'Weibull' or 'wbl'	Weibull

For a custom distribution, you must define the distribution by using pdf and cdf, logpdf and logsf, or nloglf.

mle ignores any NaN values in the censoring vector. Additionally, any NaN values in data or the frequency vector (Frequency) cause mle to ignore the corresponding values in the censoring vector.

Example: 'Censoring',censored, where censored is a vector that contains censorship information.

Data Types: logical | single | double

TruncationBounds — Truncation bounds

[-Inf,Inf] (default) | vector of two elements

Truncation bounds, specified as a vector of two elements.

mle supports truncated observations for the following built-in distributions and a custom distribution.

Distribution Value	Distribution Type
'Beta'	Beta
'BirnbaumSaunders'	Birnbaum-Saunders
'Burr'	Burr
'Exponential'	Exponential
'Extreme Value' or 'ev'	Extreme value
'Gamma'	Gamma
'Generalized Extreme Value' or 'gev'	Generalized extreme value
'Generalized Pareto' or 'gp'	Generalized Pareto
'Half Normal' or 'hn'	Half-normal
'InverseGaussian'	Inverse Gaussian
'Logistic'	Logistic
'LogLogistic'	Loglogistic
'LogNormal'	Lognormal
'Nakagami'	Nakagami
'Normal'	Normal
'Poisson'	Poisson
'Rayleigh'	Rayleigh
'Rician'	Rician
'Stable'	Stable
'tLocationScale'	t location-scale
'Weibull' or 'wbl'	Weibull

For a custom distribution, you must define the distribution by using pdf and cdf, logpdf and logsf, or nloglf.

Example: 'TruncationBounds',[0,10]

Data Types: single | double

Frequency — Frequency of observations

vector of 1s (default) | vector of nonnegative integer counts

Frequency of observations, specified as a vector of nonnegative integer counts that has the same number of rows as data. The jth element of the Frequency value gives the number of times the jth row of data was observed. The default is a vector of 1s, indicating one observation per row of data.

mle ignores any NaN values in this frequency vector. Additionally, any NaN values in data or the censoring vector (Censoring) cause mle to ignore the corresponding values in the frequency vector.

Example: 'Frequency',freq, where freq is a vector that contains the observation frequencies.

Data Types: single | double

Alpha — Significance level

0.05 (default) | scalar in the range (0,1)

Significance level for the confidence interval pci of parameter estimates, specified as a scalar in the range (0,1). The confidence level of pci is 100(1–Alpha)%. The default is 0.05 for 95% confidence.

Example: 'Alpha',0.01 specifies the confidence level as 99%.

Data Types: single | double

Options — Options for iterative algorithm

statset('mlecustom') (default) | structure

Options for the iterative algorithm, specified as a structure returned by statset.

Use this argument to control details of the maximum likelihood optimization. This argument is valid in the following cases:

• The sample data is truncated.

• The sample data includes left-censored or interval-censored observations.

• You fit a custom distribution.

The mle function interprets the following statset options for optimization.

Field Name	Description	Default Value
GradObj	Flag indicating whether fmincon can expect the nloglf custom function to return the gradient vector of the negative loglikelihood as a second output, specified as 'on' or 'off'. For an example of supplying a gradient to fmincon, see Avoid Numerical Issues When Fitting Custom Distributions. mle ignores GradObj when using fminsearch. You can specify the optimization function by using the OptimFun name-value argument. The default optimization function is fminsearch.	'off'
DerivStep	Relative difference, specified as a vector of the same size as Start and used in finite difference derivative approximations when mle uses fmincon and GradObj is 'off'. mle ignores DerivStep when using fminsearch.	eps^(1/3)
FunValCheck	Flag indicating whether mle checks the values returned by the distribution functions for validity, specified as 'on' or 'off'. A poor choice for the starting point can cause the distribution functions to return NaNs, infinite values, or out-of-range values if you define the function without suitable error checking.	'on'
TolBnd	Offset for lower and upper bounds when mle uses fmincon, specified as a positive scalar. mle treats lower and upper bounds as strict inequalities, or open bounds. When using fmincon, mle approximates the bounds by including the offset specified by TolBnd for the lower and upper bounds.	1e-6
TolFun	Termination tolerance on the function value, specified as a positive scalar.	1e-6
TolX	Termination tolerance for the parameters, specified as a positive scalar.	1e-6
MaxFunEvals	Maximum number of function evaluations allowed, specified as a positive integer.	400
MaxIter	Maximum number of iterations allowed, specified as a positive integer.	200
Display	Level of display, specified as 'off', 'final', or 'iter'. 'off' — Display no information. 'final' — Display the final information. 'iter' — Display information at each iteration	'off'

For examples of the Options name-value argument, see Find MLEs for Distribution with Finite Support and Three-Parameter Weibull Distribution.

For more details, see the options input argument of fminsearch and fmincon (Optimization Toolbox).

Example: 'Options',statset('FunValCheck','off')

Data Types: struct

Start — Initial parameter values

row vector

Initial parameter values for the Burr distribution, stable distribution, and custom distributions, specified as a row vector. The length of the Start value must be the same as the number of parameters estimated by mle.

If the sample data is truncated or includes left-censored or interval-censored observations, the Start argument is required for the Burr and stable distributions. This argument is always required when you fit a custom distribution, that is, when you use the pdf, logpdf, or nloglf name-value argument. For other cases, mle can either find initial values or compute MLEs without initial values.

Example: 0.05

Example: [100,2]

Data Types: single | double

LowerBound — Lower bounds for distribution parameters

vector of -Infs (default) | row vector

Lower bounds for the distribution parameters, specified as a row vector of the same length as Start.

This argument is valid in the following cases:

• The sample data is truncated.

• The sample data includes left-censored or interval-censored observations.

• You fit a custom distribution.

Example: 'Lowerbound',0

Data Types: single | double

UpperBound — Upper bounds for distribution parameters

vector of Infs (default) | row vector

Upper bounds for the distribution parameters, specified as a row vector of the same length as Start.

This argument is valid in the following cases:

• The sample data is truncated.

• The sample data includes left-censored or interval-censored observations.

• You fit a custom distribution.

Example: 'Upperbound',1

Data Types: single | double

OptimFun — Optimization function

'fminsearch' (default) | 'fmincon'

Optimization function used by mle to maximize the likelihood, specified as either 'fminsearch' or 'fmincon'. The 'fmincon' option requires Optimization Toolbox™.

• The sample data is truncated.

• The sample data includes left-censored or interval-censored observations.

• You fit a custom distribution.

Example: 'Optimfun','fmincon'

Output Arguments

phat — Parameter estimates

row vector

Parameter estimates, returned as a row vector. For a description of parameter estimates for the built-in distributions, see Distribution.

pci — Confidence intervals for parameter estimates

2-by-k matrix

Confidence intervals for parameter estimates, returned as a 2-by-k matrix, where k is the number of parameters estimated by mle. The first and second rows of the pci show the lower and upper confidence limits, respectively.

You can specify the significance level for the confidence interval by using the Alpha name-value argument.

More About

Censorship Types

mle supports left-censored, right-censored, and interval-censored observations.

• Left-censored observation at time t — The event occurred before time t, and the exact event time is unknown.

• Right-censored observation at time t — The event occurred after time t, and the exact event time is unknown.

• Interval-censored observation within the interval [t1,t2] — The event occurred after time t1 and before time t2, and the exact event time is unknown.

Double-censored data includes both left-censored and right-censored observations.

Survival Function

The survival function is the probability of survival as a function of time. It is also called the survivor function.

The survival function gives the probability that the survival time of an individual exceeds a certain value. Because the cumulative distribution function F(t) is the probability that the survival time is less than or equal to a given point t in time, the survival function for a continuous distribution S(t) is the complement of the cumulative distribution function: S(t) = 1 – F(t).

Tips

• When you supply custom distribution functions or use built-in distributions for left-censored, double-censored, interval-censored, or truncated observations, mle computes the parameter estimates using an iterative maximization algorithm. With some models and data, a poor choice for the starting point (Start) can cause mle to converge to a local optimum that is not the global maximizer, or to fail to converge entirely. Even in cases for which the loglikelihood is well behaved near the global maximum, the choice of starting point is often crucial to convergence of the algorithm. In particular, if the initial parameter values are far from the MLEs, underflow in the distribution functions can lead to infinite loglikelihoods.

Algorithms

• The mle function finds MLEs by minimizing the negative loglikelihood function (that is, maximizing the loglikelihood function) or by using a closed-form solution, if available. The objective function is the negative logarithm value of the product of the sample data (X) probabilities, given the distribution parameters (θ):

  $$\text{Objective Function}=-\log {\displaystyle \prod _{x\in X}P(x|\theta )}$$

  The probability function P depends on the censorship information for each observation.

  • Fully observed observation — P(x|θ) = f(x), where f is the probability density function (pdf) with the parameters θ.

  • Left-censored observation — P(x|θ) = F(x), where F is the cumulative distribution function (cdf) with the parameters θ.

  • Right-censored observation — P(x|θ) = 1 – F(x).

  • Interval-censored observation between x_L and x_U — P(x|θ) = F(x_U) – F(x_L).

  For truncated data, mle scales the distribution functions so that all the probabilities lie in the truncation bounds [L,U].

  $$f_{\text{truncation}}(x)=\{\begin{array}{l}\frac{f(x)}{F(U)-F(L)},\text{if }L\le x\le U,\hfill \\ 0,\text{Otherwise}.\hfill \end{array}$$

  $$F_{\text{truncation}}(x)=\{\begin{array}{ll}\frac{F(x)-F(L)}{F(U)-F(L)},\hfill & \text{if }L\le x\le U,\hfill \\ \begin{array}{l}0,\\ 1,\end{array}\hfill & \begin{array}{l}\text{if }x<L,\\ \text{if }x>U.\end{array}\hfill \end{array}$$

• The mle function computes the confidence intervals pci using an exact method when it is available, and when the sample data is not truncated and does not include left-censored or interval-censored observations. Otherwise, the function uses the Wald method. An exact method is available for these distributions: binomial, discrete uniform, exponential, normal, lognormal, Poisson, Rayleigh, and continuous uniform.

Extended Capabilities

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Usage notes and limitations:

• You cannot specify the name-value argument Distribution as 'Rician' or 'Stable'.

• If you fit a custom distribution by using the pdf and cdf, logpdf and logsf, or nloglf name-value arguments, the custom distribution function must support GPU arrays.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a