dsphdl.CICInterpolator
Description
The dsphdl.CICInterpolator
System object™ interpolates an input signal by using a cascaded integrator-comb (CIC)
interpolation filter. CIC interpolation filters are a class of linear phase finite impulse
response (FIR) filters consisting of a comb part and an integrator part. The CIC interpolation
filter structure consists of N sections of cascaded comb filters, a rate
change factor of R, and N sections of cascaded
integrators. For more information about CIC interpolation filters, see Algorithms.
The System object supports these combinations of input and output data.
Scalar input and scalar output — Support for fixed and variable interpolation rates
Scalar input and vector output — Support for fixed interpolation rates only
Vector input and vector output — Support for fixed interpolation rates only
The System object provides an architecture suitable for HDL code generation and hardware deployment.
The System object supports real and complex fixed-point inputs.
To filter input data with a CIC interpolator filter, follow these steps:
Create the
dsphdl.CICInterpolatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a MATLAB® script, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the System object.
Creation
Description
cicIntFilt = dsphdl.CICInterpolatorcicIntFilt, with default properties.
cicIntFilt = dsphdl.CICInterpolator(Name=Value)
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Specify whether the System object operates with a fixed or variable interpolation rate.
'Property'— Use a fixed interpolation rate specified by theInterpolationFactorproperty.'Input port'— Use a variable interpolation rate specified by theRinput argument.
Note
The System object does not support variable interpolation for these two combinations of input and output:
Scalar input and vector output
Vector input and vector output
Specify the interpolation factor as an integer from 1 to 2048. The range of available values depends on the type of input and output data. This value gives the rate at which the System object interpolates the input.
| Input Data | Output Data | InterpolationFactor Valid Values |
|---|---|---|
| Scalar | Scalar | Integer from 1 to 2048 |
| Scalar | Vector | Integer from 1 to 64 |
| Vector | Vector | Integer from 1 to 64 |
Note
For vector inputs, select the interpolation factor rate and input vector length such that their multiplication value does not exceed 64.
Dependencies
To enable this property, set the InterpolationSource property to 'Property'.
Specify the upper bound of the range of valid values for the R
input argument as an integer from 1 to 2048.
Note
The System object does not support variable interpolation for these two combinations of input and output:
Scalar input and vector output
Vector input and vector output
Dependencies
To enable this property, set the InterpolationSource property to 'Input port'.
Specify the differential delay of the comb part of the filter as either
1 or 2 cycles.
Specify the number of sections in either the comb part or the integrator part of the System object.
Specify the minimum number of cycles between the valid input samples as
1, factors of R, or multiples of
R based on the type of input and output data, where
R is the interpolation factor.
| Input Data | Output Data | Minimum Number of Cycles Between Valid Input Samples |
|---|---|---|
| Scalar | Scalar | greater than or equal to R |
| Scalar | Vector | factors less than R |
| Vector | Vector | 1 |
Dependencies
To enable this property, set the InterpolationSource property to 'Property'.
Set this property to true to compensate for the output gain of
the filter.
The latency of the System object changes depending on the type of interpolation you specify, the number of sections, and the value of this property. For more information on the latency of the System object, see Latency.
Choose the data type of the filtered output data.
'Full precision'— The output data type has a word length equal to the input word length plus gain bits.'Same word length as input'— The output data type has a word length equal to the input word length.'Minimum section word lengths'— The output data type uses the word length you specify in the OutputWordLength property.
Word length of the output, specified as an integer from 2 to 104.
Dependencies
To enable this property, set the OutputDataType property to 'Minimum section word
lengths'.
When you set this property to true, the System object expects a reset input
argument.
Usage
Syntax
Description
[
filters the input data when dataOut,validOut] = cicIntFilt(dataIn,validIn,R,reset)reset is false and
clears filter internal states when reset is true.
The System object expects the reset argument only when you set the
ResetInputPort
property to true. The InterpolationSource property
must be set to 'Input port'.
Input Arguments
Specify input data as a scalar or a column vector with a length from 1 to 64. The input data must be a signed integer or signed fixed point with a word length less than or equal to 32.
While processing the input data, the System object implements the rounding method Floor and the overflow
action Wrap. For more details, see Rounding Modes and Overflow Handling.
Data Types: int8 | int16 | int32 | fi
Complex Number Support: Yes
Control signal that indicates if the input data is valid. When
validIn is 1 (true), the
object captures the values from the dataIn argument. When
validIn is 0 (false), the
object ignores the values from the dataIn argument.
Data Types: logical
Use this argument to dynamically specify the variable interpolation rate during run time.
This value must have the data type fi(0,12,0) and must be an
integer in the range from 1 to the MaxInterpolationFactor
property value.
Dependencies
To enable this argument, set the InterpolationSource property to 'Input
port'.
Data Types: fi(0,12,0)
Control signal that clears internal states. When reset is
1 (true), the object stops the current
calculation and clears internal states. When the reset is
0 (false) and the input
valid is 1 (true), the
object captures data for processing.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Dependencies
To enable this argument, set the ResetInputPort
property to true.
Data Types: logical
Output Arguments
CIC-interpolated output data, returned as a scalar or a column vector with a length from 1 to 64.
The OutputDataType property sets the data type of this argument.
Data Types: int8 | int16 | int32 | fi
Complex Number Support: Yes
Control signal that indicates if the output data is valid. When
validOut is 1 (true), the
object returns valid data from the dataOut argument. When
validOut is 0 (false),
values from the dataOut argument are not valid.
Data Types: logical
Control signal that indicates that the object is ready for new input data sample
on the next cycle. When ready is 1
(true), you can specify the data
and valid inputs for the next time step. When
ready is 0
(false), the object ignores any input data in the next time step.
Data Types: logical
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
getLatency | Latency of CIC interpolation filter |
Examples
This example shows how to use a dsphdl.CICInterpolator System object™ to filter and upsample data. This object supports scalar and vector inputs. In this example, two functions are provided to work with scalar and vector input data separately. You can generate HDL code from these functions.
Generate Frames of Random Input Samples
Set up workspace variables for the object to use. The object supports fixed and variable interpolation rates for scalar inputs and only a fixed interpolation rate for vector inputs. The example runs the HDLCICInterp_maxR8 function when you set the scalar variable to true and runs the HDLCICInterp_vec function when you set the scalar variable to false. For scalar inputs, choose a range of the input varRValue values and set the interpolation factor value R to the maximum expected interpolation factor. For vector inputs, the input data must be a column vector of size 1 to 64 and R must be an integer multiple of the input frame size.
R = 8; % interpolation factor M = 1; % differential delay N = 3; % number of sections scalar = true; % true for scalar; false for vector if scalar varRValue = [2, 4, 5, 6, 7, 8]; vecSize = 1; else varRValue = R; %#ok fac = (factor(R)); vecSize = fac(randi(length(fac),1,1)); end numFrames = length(varRValue); dataSamples = cell(1,numFrames); varRtemp = cell(1,numFrames); framesize = zeros(1,numFrames); refOutput = []; WL = 0; % Word length FL = 0; % Fraction length
Generate Reference Output from dsp.CICInterpolator System Object
Generate frames of random input samples and apply the samples to the dsp.CICInterpolator System object. Later in this example, you use the output generated by the System object as reference data for comparison. The System object does not support a variable interpolation rate, so you must create and release the object for each change in interpolation factor value.
totalsamples = 0; for i = 1:numFrames framesize(i) = varRValue(i)*randi([5 20],1,1); dataSamples{i} = fi(randn(vecSize,framesize(i)),1,16,8); ref_cic = dsp.CICInterpolator(DifferentialDelay=M, ... NumSections=N, ... InterpolationFactor=varRValue(i)); refOutput = [refOutput,ref_cic(dataSamples{i}(:)).']; %#ok release(ref_cic); end
Run Function Containing dsphdl.CICInterpolator System Object
Set the properties of the System object to match the input data parameters and run the function for your input type. These functions operate on a stream of data samples rather than a frame. You can generate HDL code from these functions.
The example uses the HDLCICInterp_maxR8 function for a scalar input.
function [dataOut,validOut] = HDLCICInterp_maxR8(dataIn,validIn,R) %HDLCICInterp_maxR8 % Performs CIC interpolation with an input interpolation factor up to 8. % sampleIn is a scalar fixed-point value. % validIn is a logical scalar value. persistent cic8; if isempty(cic8) cic8 = dsphdl.CICInterpolator(InterpolationSource='Input port', ... MaxInterpolationFactor=8, ... DifferentialDelay=1, ... NumSections=3); end [dataOut,validOut] = cic8(dataIn,validIn,R); end % Copyright 2021-2023 The MathWorks, Inc.
The example uses the HDLCICInterp_vec function for a vector input.
function [dataOut,validOut] = HDLCICInterp_vec(dataIn,validIn) %HDLCICInterp_vec % Performs CIC interpolation with an input vector. % sampleIn is a fixed-point vector. % validIn is a logical scalar value. persistent cicVec; if isempty(cicVec) cicVec = dsphdl.CICInterpolator(InterpolationSource='Property', ... InterpolationFactor=8, ... DifferentialDelay=1, ... NumSections=3); end [dataOut,validOut] = cicVec(dataIn,validIn); end % Copyright 2021-2023 The MathWorks, Inc.
To flush the remaining data, run the object by inserting the required number of idle cycles after each frame using the latency variable. For more information, see the GainCorrection property.
Initialize the output to a size large enough to accommodate the output data. The final size is smaller than totalsamples due to interpolation.
if scalar latency = 3 + N + 2*R + 9; dataOut = zeros(1,totalsamples*R+numFrames*latency); else latency = 3 + (N*(vecSize*R))+ 3*N + 9; %#ok dataOut = zeros(vecSize*R,totalsamples+numFrames*latency); end validOut = zeros(1,size(dataOut,2)); idx=0; for ij = 1:numFrames if scalar dataIn = upsample([0 0 dataSamples{ij}],R); validIn = upsample([true false true(1,length(dataSamples{ij}))],R); % scalar input with variable interpolation for ii = 1:length(validIn) idx = idx+1; [dataOut(:,idx),validOut(idx)] = HDLCICInterp_maxR8( ... dataIn(ii), ... validIn(ii), ... fi(varRValue(ij),0,12,0)); end for ii = 1:latency idx = idx+1; [dataOut(:,idx),validOut(idx)] = HDLCICInterp_maxR8( ... fi(0,1,16,8), ... false, ... fi(varRValue(ij),0,12,0)); end else % vector input with fixed interpolation for ii = 1:size(dataSamples{ij},2) %#ok idx = idx+1; [dataOut(:,idx),validOut(idx)] = HDLCICInterp_vec( ... dataSamples{ij}(:,ii), ... true); end for ii = 1:latency idx = idx+1; [dataOut(:,idx),validOut(idx)] = HDLCICInterp_vec( ... fi(zeros(vecSize,1),1,16,8), ... false); end end end
Compare Function Output with Reference Data
Compare the function results against the output from the dsp.CICInterpolator object.
cicOutput = dataOut(:,validOut==1); refOutput = refOutput(:); fprintf('\nCIC Interpolator\n'); difference = (abs(cicOutput(:)-refOutput(1:numel(cicOutput)))>0); fprintf(['\nTotal number of samples differed between Behavioral ' ... 'and HDL simulation: %d \n'],sum(difference));
The latency of the dsphdl.CICInterpolator System object™ varies depending on how many integrator and comb sections your filter has, the input vector size, and whether you enable gain correction. Use the getLatency function to find the latency of a particular filter configuration. The latency is the number of cycles between the first valid input and the first valid output, assuming the input is continuously valid.
Create a dsphdl.CICInterpolator System object and request the latency. The default System object filter has two integrator and comb sections, and the gain correction is disabled.
hdlcic = dsphdl.CICInterpolator
hdlcic =
dsphdl.CICInterpolator with properties:
InterpolationSource: 'Property'
InterpolationFactor: 2
DifferentialDelay: 1
NumSections: 2
NumCycles: 1
GainCorrection: false
Show all properties
L_def = getLatency(hdlcic)
L_def = 14
Modify the filter object so it has three integrator and comb sections. Check the resulting change in latency.
hdlcic.NumSections = 3; L_3sec = getLatency(hdlcic)
L_3sec = 19
Enable the gain correction on the filter object with vector input size 2. Check the resulting change in latency.
hdlcic.GainCorrection = true; vecSize = 2; L_wgain = getLatency(hdlcic,vecSize)
L_wgain = 33
Algorithms
The transfer function of a CIC interpolation filter is
HC is the transfer function of the comb part of the CIC filter.
HI is the transfer function of the integrator part of the CIC filter.
N is the number of sections in either the comb part or integrator part of the filter. This value does not represent the total number of sections throughout the entire filter.
R is the interpolation factor.
M is the differential delay.
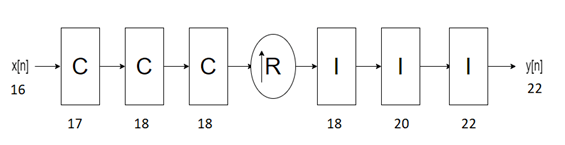
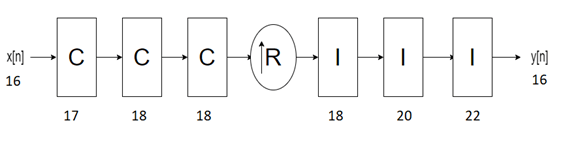
The dsphdl.CICInterpolator
System object has the CIC filter structure shown in this figure. The structure consists of
N sections of cascaded comb filters, a rate change factor of
R, and N sections of cascaded integrators [1].

You can locate the unit delay in the integrator part of the CIC filter in either the feedforward or feedback path. These two configurations yield an identical filter frequency response. However, the numerical outputs from these two configurations are different due to the latency of the paths. Because this configuration is preferred for HDL implementation, this System object puts the unit delay in the feedforward path of the integrator.
The System object upsamples the comb stage output using R, either using the
fixed interpolation rate provided using the InterpolationFactor property or the variable interpolation rate provided using
the R input
argument. At the upsampling stage, the System object uses a counter to count the valid input samples, which depend on the
interpolation rate. Whenever the interpolation rate changes, the System object resets and starts a new calculation from the next sample. This mechanism
prevents the object from accumulating false values. Then, the System object provides the interpolated output to the integrator part of the CIC
filter.
The gain of the CIC interpolation filter at each stage is given by
Gi is the gain at ith stage.
R is the
InterpolationFactorproperty value.M is the
DifferentialDelayproperty value.N is the
NumSectionsproperty value.
The output of the System object is amplified by a specific gain value. This gain equals the gain of the 2Nth stage of the CIC interpolation filter and is given by .
The System object implements gain correction in two parts: coarse gain and fine gain. In coarse gain correction, the System object calculates the shift value, adds the shift value to the fractional bits to create a numeric type, and performs a bit-shift left and reinterpretcast. In fine gain correction, the System object divides the remaining gain with the coarse gain if the gain is not a power of 2. Then, the System object multiplies the corrected coarse gain value by the inverse value of the fine gain. Before the System object starts processing, all possible shift and fine gain values are precalculated and stored in an array.
You can modify this equation to . In this equation, cGain is the coarse gain and fGain is the fine gain. These gains are given by these equations.
To perform gain correction when the InterpolationSource property is
set to 'Input port', the System object sets the output data type configured with the maximum interpolation rate and
bit-shifts left for all of the values under the maximum interpolation rate. The bit-shift
value is equal to .
This section explains how the System object outputs data is based on the output data type selection. Consider a System object with R, M, and N values of 8, 1, and 3, respectively, and an input width of 16. The word length at the ith stage is calculated as , where:
Gi is the gain at ith stage.
BIn is the input word length.
Bi is the word length at ith stage.
The output word length is calculated as , where BOut is the output word length.
When you set the OutputDataType property to 'Full
precision', the System object returns data with a word length of 22 by adding 6 gain bits to the input word
length of 16. The word lengths of the internal comb and integrator stages are set to
accommodate the bit growth.
When you set the OutputDataType property to 'Same word
length as input', the object outputs data with a word length of 16, which is the
same length as the input word length. The word lengths of the internal comb and integrator
stages are set in the same way as in 'Full precision' mode.
When you set the OutputDataType property to 'Minimum
section word lengths' and the OutputWordLength to
16, the System object returns data with a word length of 16. The word lengths of the internal comb
and integrator stages are set in the same way as in 'Full precision'
mode.

The latency of the System object changes depending on the type of input, the interpolation you specify, the
value of the NumSections property, GainCorrection
property, and the NumCycles property. This table shows the latency of
the System object. N is the number of sections, vecLen is
the length of the vector, and R is the interpolation factor.
Common latency is equal to 2 + (N x (vecLen x R)) + 3 x N, when R is equal to 1 and it is equal to 3 + (N x (vecLen x R)) + 3 x N, when R is greater than 1.
| Input Data | Output Data | Interpolation Type | Gain Correction | Minimum number of cycles between valid input samples (NumCycles) | Latency in Clock Cycles |
|---|---|---|---|---|---|
| Scalar | Scalar | Fixed | off | NumCycles = R and > R | 3 + N. 2 + N, when R = 1. |
on | NumCycles = R and > R | 3 + N + 9. 2 + N + 9, when R = 1. | |||
| Scalar | Scalar | Variable | off | NA | 3 + N + 2 x Rmax. 2 + N, when Rmax = 1. |
on | NA | 2 + N + 2 x Rmax + 9. 2 + N + 9, when Rmax = 1. | |||
| Scalar | Vector | Fixed | off | NumCycles = 1 | Common latency + 1, when R is greater than N. Common latency, when R is less than or equal to N. Common latency – (1 + floor(N/(3 x R))), when R is less than N and (vecLen == 2 && (R == 2 && (N == 4 || N == 5 || N == 6)) || (R== 3 && N == 6)). |
| NumCycles < R | 3 + N + ((R + 1) x N + 2) + 1 + (N – 1) x NumCycles. | ||||
on | NumCycles = 1 | Common latency + 1 + 9, when R is greater than N. Common latency + 9, when R is less than or equal to N. Common latency – (1 + floor(N/(3 x R))) + 9, when R is less than N and (vecLen == 2 && (R == 2 && (N == 4 || N == 5 || N == 6)) || (R == 3 && N == 6)). | |||
| NumCycles < R | 3 + N + ((R + 1) x N + 2) + 1 + (N – 1) x NumCycles + 9. | ||||
| Vector | Vector | Fixed | off | NumCycles = 1 | Common latency Common latency – 1, when (vecLen == 2 && (R == 2 && (N == 4 || N == 5 || N == 6)) || (R== 3 && N == 6)) || (vecLen == 3 && (R == 2 && N == 6)). Common latency – ((N >1) + (N > 4)), when R = 1 and vecLen == 2. Common latency – ((N > (vecLen – 1)), when R = 1 and vecLen > 2. |
on | NumCycles = 1 | Common latency + 9. Common latency – 1 + 9, when (vecLen == 2 && (R == 2 && (N == 4 || N == 5 || N == 6)) || (R== 3 && N == 6)) || (vecLen == 3 && (R == 2 && N == 6)). Common latency – ((N >1) + (N > 4)) + 9, when R = 1 and vecLen == 2. Common latency – ((N > (vecLen – 1)) + 9, when R = 1 and vecLen > 2. |
Note
The System object does not support variable interpolation for these two combinations of input and output:
Scalar input and vector output
Vector input and vector output
This section shows the output of the System object for a scalar input with different R, M, and N values.
This figure shows the output of the System object with the default configuration (that is, with a fixed interpolation rate and R, M, and N values of 2, 1, and 2, respectively). The latency of the System object is 5 clock cycles and is calculated as 3 + N, where N is the number of sections.

This figure shows the output of the System object with a fixed interpolation rate, R, M,
and N values of 8, 1, and 3, respectively, and
GainCorrection set to true. The latency of the
object is 15 clock cycles and is calculated as 3 + N + 9, where
N is the number of sections.

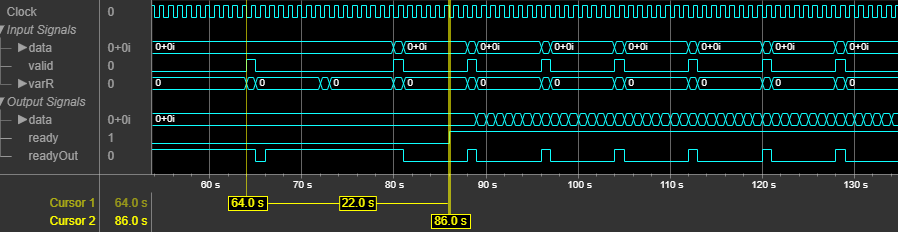
This figure shows the output of the System object with variable interpolation rate (R input argument)
values of 2, 4, and 8 and with M and N values of 1
and 3, respectively. In this case, the GainCorrection property is set
to false. The System object accepts R argument value changes only when
validIn is 1 (true). The
latency of the System object is 22 clock cycles and is calculated as 3 + N + 2 x
Rmax, where N is the
number of sections and Rmax is the maximum
interpolation factor.
This section shows the output of the System object for a vector input with different R, M, and N values.
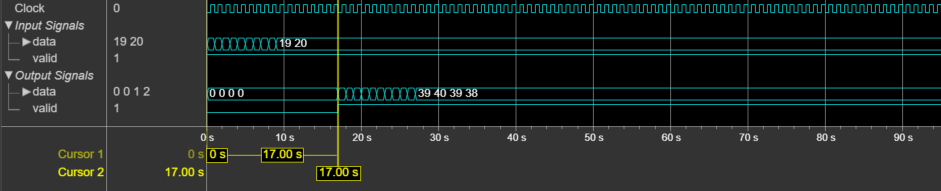
This figure shows the output of the System object for a two-element column vector input with the default configuration, that is, with a fixed interpolation rate and R, M, and N values of 2, 1, and 2, respectively. The latency of the System object is 38 clock cycles.
This figure shows the output of the System object for an eight-element column vector input with a fixed interpolation rate,
R, M, and N values of 8, 1, and
3, respectively, and the GainCorrection property to
true. The latency of the System object is 209 clock cycles.

The performance of the synthesized HDL code varies with your target and synthesis options. It also depends on the input data type.
This table shows the resource and performance data synthesis results of the System object for a scalar input with fixed and variable interpolation rates and for a
two-element column vector of type fixdt(1,16,0) with a fixed
interpolation rate when R, M, and N
are 2, 1, and 2, respectively. The generated HDL code is targeted to the AMD®
Zynq®- 7000 ZC706 Evaluation Board.
| Input Data | Interpolation Type | Slice LUTs | Slice Registers | Maximum Frequency in MHz |
|---|---|---|---|---|
| Scalar | Fixed rate | 68 | 90 | 844.12 |
| Variable rate | 143 | 115 | 451.83 | |
| Vector | Fixed rate | 480 | 921 | 376.51 |
The resources and frequencies vary based on the type of input data, and the values of R, M, and N, as well as other properties.
References
[1] Hogenauer, E. “An Economical Class of Digital Filters for Decimation and Interpolation.” IEEE Transactions on Acoustics, Speech, and Signal Processing 29, no. 2 (April 1981): 155–62. https://doi.org/10.1109/TASSP.1981.1163535.
Extended Capabilities
This System object supports C/C++ code generation for accelerating MATLAB simulations, and for DPI component generation.
The software supports double and
single data types for simulation, but not for HDL code generation.
To generate HDL code from predefined System objects, see Generate HDL Code for IIR Filter.
Version History
Introduced in R2022a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)