dsphdl.CICDecimator
Decimate signal using CIC filter
Description
The dsphdl.CICDecimator
System object™ decimates an input signal by using a cascaded integrator-comb (CIC) decimation
filter. CIC filters are a class of linear phase finite impulse response (FIR) filters
consisting of a comb part and an integrator part. The CIC decimation filter structure consists
of N sections of cascaded integrators, a rate change factor of
R, and N sections of cascaded comb filters. For more
information about CIC decimation filters, see Algorithms.
The System object supports these combinations of input and output data.
Scalar input and scalar output — Support for fixed and variable decimation rates
Vector input and scalar output — Support for fixed decimation rates only
Vector input and vector output — Support for fixed decimation rates only
The System object provides an architecture suitable for HDL code generation and hardware deployment.
The System object supports real and complex fixed-point inputs.
To filter input data with an HDL-optimized CIC decimation filter, follow these steps:
Create the
dsphdl.CICDecimatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a MATLAB® script, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the System object.
Creation
Description
cicDecFilt = dsphdl.CICDecimatorcicDecFilt, with default properties.
cicDecFilt = dsphdl.CICDecimator(Name=Value)
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Specify whether the System object operates with a fixed or variable decimation rate.
'Property'— Use a fixed decimation rate specified by theDecimationFactorproperty.'Input port'— Use a variable decimation rate specified by theRinput argument.
For vector inputs, the System object does not support a variable decimation rate.
Specify the decimation factor as an integer from 1 to 2048. This value gives the rate at which the System object decimates the input.
Dependencies
To enable this property, set the DecimationSource property to
'Property'.
Specify the upper bound of the range of valid values for the R
input argument as an integer from 1 to 2048.
Note
For vector inputs, the System object does not support variable decimation.
Dependencies
To enable this property, set the DecimationSource property to
'Input port'.
Specify the differential delay of the comb part of the filter as either
1 or 2 cycles.
Specify the number of sections in either the integrator or the comb part of the System object.
Set this property to true to compensate for the output gain of
the filter.
The latency of the System object varies depending on the type of input, the decimation you specify, the number of sections, and the value of this property. For more information on the latency of the System object, see Latency.
Choose the data type of the filtered output data.
'Full precision'— The output data type has a word length equal to the input word length plus gain bits.'Same word length as input'— The output data type has a word length equal to the input word length.'Minimum section word lengths'— The output data type uses the word length you specify in theOutputWordLengthproperty. When you choose this option, the System object applies a pruning algorithm internally. For more information about pruning, see Output Data Type.
Word length of the output, specified as an integer from 2 to 104.
Note
When this value is 2, 3,
4, 5, or 6, the
System object can overflow the output data.
Dependencies
To enable this property, set the OutputDataType property to
'Minimum section word lengths'.
When you set this property to true, the System object expects a reset input argument.
Usage
Syntax
Description
[
filters the input data when dataOut,validOut] = cicDecFilt(dataIn,validIn,R,reset)reset is false and
clears filter internal states when reset is true.
The System object expects the reset argument only when you set the
ResetInputPort property to true. The
DecimationSource property must be set to 'Input
port'.
Input Arguments
Specify input data as a scalar or a column vector with a length from 1 to 64. The
input data must be a signed integer or signed fixed point with a word length less than
or equal to 32. The DecimationFactor property must be an integer
multiple of the input frame size.
While processing the input data, the System object implements the rounding method Floor and the overflow
action Wrap. For more details, see Rounding Modes and Overflow Handling.
Data Types: int8 | int16 | int32 | fi
Complex Number Support: Yes
Control signal that indicates if the input data is valid. When
validIn is 1 (true), the
object captures the values from the dataIn argument. When
validIn is 0 (false), the
object ignores the values from the dataIn argument.
Data Types: logical
Specify the decimation rate.
The R value must have the data type
fi(0,12,0) and it must be an integer in the range from 1 to the
MaxDecimationFactor property value.
Dependencies
To enable this argument, set the DecimationSource
property to 'Input port'.
Data Types: fi(0,12,0)
Control signal that clears internal states. When reset is
1 (true), the object stops the current
calculation and clears internal states. When the reset is
0 (false) and the input
valid is 1 (true), the
object captures data for processing.
For more reset considerations, see the Reset Signal section on the Hardware Control Signals page.
Dependencies
To enable this argument, set the ResetInputPort
property to true.
Data Types: logical
Output Arguments
CIC-decimated output data, returned as a scalar or a column vector with a length from 1 to 64.
The OutputDataType property sets the data type of this argument. See Output Data Type.
Data Types: int8 | int16 | int32 | fi
Complex Number Support: Yes
Control signal that indicates if the output data is valid. When
validOut is 1 (true), the
object returns valid data from the dataOut argument. When
validOut is 0 (false),
values from the dataOut argument are not valid.
Data Types: logical
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
getLatency | Latency of CIC decimation filter |
Examples
This example shows how to use a dsphdl.CICDecimator System object™ to filter and downsample data. This object supports scalar and vector inputs. In this example, two functions are provided to work with scalar and vector inputs separately. You can generate HDL code from these functions.
Generate Frames of Random Input Samples
Set up workspace variables for the object to use. The object supports fixed and variable decimation rates for scalar inputs and only a fixed decimation rate for vector inputs. The example runs the HDLCIC_maxR8 function when you set the scalar variable to true and runs the HDLCIC_vec function when you set the scalar variable to false. For scalar inputs, choose a range of the input varRValue values and set the decimation factor value R to the maximum expected decimation factor. For vector inputs, the input data must be a column vector of size 1 to 64 and R must be an integer multiple of the input frame size.
R = 8; % decimation factor M = 1; % differential delay N = 3; % number of sections scalar = true; % true for scalar; false for vector if scalar varRValue = [2, 4, 5, 6, 7, 8]; vecSize = 1; else varRValue = R; %#ok fac = (factor(R)); vecSize = fac(randi(length(fac),1,1)); end numFrames = length(varRValue); dataSamples = cell(1,numFrames); varRtemp = cell(1,numFrames); framesize = zeros(1,numFrames); refOutput = []; WL = 0; % Word length FL = 0; % Fraction length
Generate Reference Output from dsp.CICDecimator System Object
Generate frames of random input samples and apply the samples to the dsp.CICDecimator System object. Later in this example, you use the output generated by the System object as reference data for comparison. The System object does not support a variable decimation rate, so you must create and release the object for each change in decimation factor value.
totalsamples = 0; for i = 1:numFrames framesize(i) = varRValue(i)*randi([5 20],1,1); dataSamples{i} = fi(randn(vecSize,framesize(i)),1,16,8); ref_cic = dsp.CICDecimator(DifferentialDelay=M, ... NumSections=N, ... DecimationFactor=varRValue(i)); refOutput = [refOutput,ref_cic(dataSamples{i}(:)).']; %#ok release(ref_cic); end
Run Function Containing dsphdl.CICDecimator System Object
Set the properties of the System object to match the input data parameters and run the function for your input type. These functions operate on a stream of data samples rather than a frame. You can generate HDL code from these functions.
The example uses the HDLCIC_maxR8 function for a scalar input.
function [dataOut,validOut] = HDLCIC_maxR8(dataIn,validIn,R) %HDLCIC_maxR8 % Performs CIC decimation with an input decimation factor up to 8. % dataIn is a scalar fixed-point value. % validIn is a logical scalar value. persistent cic8; if isempty(cic8) cic8 = dsphdl.CICDecimator(DecimationSource='Input port', ... MaxDecimationFactor=8, ... DifferentialDelay=1, ... NumSections=3); end [dataOut,validOut] = cic8(dataIn,validIn,R); end % Copyright 2021-2023 The MathWorks, Inc.
The example uses the HDLCIC_vec function for a vector input.
function [dataOut,validOut] = HDLCIC_vec(dataIn,validIn) %HDLCIC_vec % Performs CIC decimation with an input vector. % dataIn is a fixed-point vector. % validIn is a logical scalar value. persistent cicVec; if isempty(cicVec) cicVec = dsphdl.CICDecimator(DecimationSource='Property', ... DecimationFactor=8, ... DifferentialDelay=1, ... NumSections=3); end [dataOut,validOut] = cicVec(dataIn,validIn); end % Copyright 2021-2023 The MathWorks, Inc.
To flush the remaining data, run the object by inserting the required number of idle cycles after each frame using the latency variable. For more information, see Latency.
Initialize the output to a size large enough to accommodate the output data. The final size is smaller than totalsamples due to decimation.
latency = floor((vecSize - 1)*(N/vecSize)) + 1 + N + (2+(vecSize+1)*N) + 9; dataOut = zeros(1,totalsamples+numFrames*latency); validOut = zeros(1,totalsamples+numFrames*latency); idx=0; for ij = 1:numFrames if scalar % scalar input with variable decimation for ii = 1:length(dataSamples{ij}) idx = idx+1; [dataOut(idx),validOut(idx)] = HDLCIC_maxR8( ... dataSamples{ij}(ii), ... true, ... fi(varRValue(ij),0,12,0)); end for ii = 1:latency idx = idx+1; [dataOut(idx),validOut(idx)] = HDLCIC_maxR8( ... fi(0,1,16,8), ... false, ... fi(varRValue(ij),0,12,0)); end else % vector input with fixed decimation for ii = 1:size(dataSamples{ij},2) %#ok idx = idx+1; [dataOut(idx),validOut(idx)] = HDLCIC_vec( ... dataSamples{ij}(:,ii), ... true); end for ii = 1:latency idx = idx+1; [dataOut(idx),validOut(idx)] = HDLCIC_vec( ... fi(zeros(vecSize,1),1,16,8), ... false); end end end
Compare Function Output with Reference Data
Compare the function results against the output from the dsp.CICDecimator object.
cicOutput = dataOut(validOut==1); fprintf('\nCIC Decimator\n'); difference = (abs(cicOutput-refOutput(1:length(cicOutput)))>0); fprintf(['\nTotal number of samples differed between Behavioral ' ... 'and HDL simulation: %d \n'],sum(difference));
CIC Decimator Total number of samples differed between Behavioral and HDL simulation: 0
The latency of the dsphdl.CICDecimator System object™ varies depending on how many integrator and comb sections your filter has, the input vector size, and whether you enable gain correction. Use the getLatency function to find the latency of a particular filter configuration. The latency is the number of cycles between the first valid input and the first valid output, assuming the input is continuously valid.
Create a dsphdl.CICDecimator System object and request the latency. The default System object filter has two integrator and comb sections, and the gain correction is disabled.
hdlcic = dsphdl.CICDecimator
hdlcic =
dsphdl.CICDecimator with properties:
DecimationSource: 'Property'
DecimationFactor: 2
DifferentialDelay: 1
NumSections: 2
GainCorrection: false
Show all properties
L_def = getLatency(hdlcic)
L_def = 5
Modify the filter object so it has three integrator and comb sections. Check the resulting change in latency.
hdlcic.NumSections = 3; L_3sec = getLatency(hdlcic)
L_3sec = 6
Enable the gain correction on the filter object with vector input size 2. Check the resulting change in latency.
hdlcic.GainCorrection = true; vecSize = 2; L_wgain = getLatency(hdlcic,vecSize)
L_wgain = 25
Algorithms
The transfer function of a CIC decimation filter is
HI is the transfer function of the integrator part of the CIC filter.
HC is the transfer function of the comb part of the CIC filter.
N is the number of sections. The number of sections in a CIC filter is defined as the number of sections in either the comb part or the integrator part of the filter. This value does not represent the total number of sections throughout the entire filter.
R is the decimation factor.
M is the differential delay.
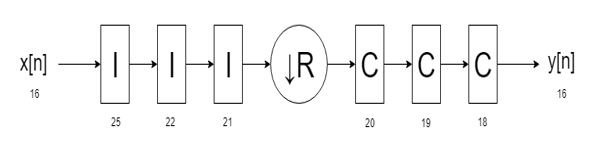
The dsphdl.CICDecimator
System object has the CIC filter structure shown in this figure. The structure consists of
N sections of cascaded integrators, a rate change factor of
R, and N sections of cascaded comb filters [1].

Designs can put the unit delay in the integrator part of the CIC filter in either the feedforward or feedback path. These two configurations yield an identical filter frequency response. However, the numerical outputs from these two configurations are different due to the latency of the paths. This System object puts the unit delay in the feedforward path of the integrator.
The System object downsamples the integrator stage output using R, either
based on the fixed decimation rate provided using the DecimationFactor property or
the variable decimation rate provided using the R input argument. At the
downsampler stage, the System object uses a counter to count the valid input samples, which depend on the
decimation rate. Whenever the decimation rate changes, the object resets and starts a new
calculation from the next sample. This mechanism prevents the System object from accumulating invalid values. Then, the System object provides the decimated output to the comb part.
The gain of the System object is given by .
R is the
DecimationFactorproperty value.M is the
DifferentialDelayproperty value.N is the
NumSectionsproperty value.
The System object implements gain correction in two parts: coarse gain and fine gain. In coarse gain correction, the System object calculates the shift value, adds the shift value to the fractional bits to create a numeric type, and then performs a bit-shift left. In fine gain correction, the System object divides the remaining gain with the coarse gain if the gain is not a power of 2 and then multiplies the coarse gain corrected value with the inverse value of fine gain. All possible shift and fine gain values are precalculated and stored in an array before the System object starts processing.
You can modify this equation as , where cGain means coarse gain and fGain means fine gain.
To perform GainCorrection when the
InterpolationSource property is set to 'Input
port', the System object sets the output data type configured with the maximum decimation rate and
bit-shifts left for all the values under the maximum decimation rate. The bit-shift value is
equal to .
This section explains how the System object determines the output data type. For example, consider a filter with
DecimationFactor, DifferentialDelay, and
NumSections values of 8, 1, and 3, respectively, with an input width
of 16 bits.
The output word length is calculated as .
BIn is the input word length.
BOut is the output word length.
When you set the OutputDataType property to 'Full
precision', the System object returns data with a word length of 25 bits, by adding nine gain bits to the
input word length.

When you set the OutputDataType property to 'Same word
length as input', the object outputs data with a word length of 16, which is the
same length as the input word length. The internal integrator and comb stages use the
full-precision data type with 25 bits.

When you set the OutputDataType property to 'Minimum
section word lengths' and the OutputWordLength property to
16, the System object returns data with a word length of 16 bits. In this case, the object changes
the bit width at each stage, based on the pruning algorithm.
If the OutputWordLength property value is less than the number of
bits requested at the output, the least significant bits (LSBs) at the earlier stages are
pruned. The Hogenauer algorithm provides the number of LSBs to discard at each stage. This
algorithm minimizes the loss of information in the output data [1].
The latency of the System object varies depending on the type of input, the decimation you specify, the number
of sections, and the value of the GainCorrection property. This table
shows the latency of the System object. N is the number of sections and vecLen
is the length of the vector.
| Input Data | Output Data | Decimation Type | Gain Correction | Latency in Clock Cycles |
|---|---|---|---|---|
| Scalar | Scalar | Fixed | off | 3 + N. When R = 1, 2 + N. |
on | 3 + N + 9. When R = 1, 2 + N + 9. | |||
| Scalar | Scalar | Variable | off | 4 + N. When Rmax = 1, 3 + N. |
on | 4 + N + 9. When Rmax = 1, 3 + N + 9. | |||
| Vector | Scalar | Fixed | off | floor((vecLen – 1) x
(N/vecLen)) + 1 + N + (2
+ (vecLen + 1) x N |
on | floor((vecLen – 1) x
(N/vecLen)) + 1 + N + (2
+ (vecLen + 1) x N) + 9 | |||
| Vector | Vector | Fixed | off | floor((vecLen – 1) x
(N/vecLen)) + 1 + N + (2
+ (vecLen + 1) x N |
on | floor((vecLen – 1) x
(N/vecLen)) + 1 + N + (2
+ (vecLen + 1) x N) + 9 |
Note
For vector inputs, the System object does not support variable decimation.
This section shows the output of the System object for a scalar input with different R, M, and N values.
This figure shows the output of the System object with the default configuration, that is, with a fixed decimation rate and
DecimationFactor, DifferentialDelay, and
NumSections values of 2, 1, and 2, respectively. The System object returns valid output data at every second cycle based on the fixed DecimationFactor value of 2.
The latency of the System object is 5 clock cycles, calculated as 3 + N.

This figure shows the output of the System object with a fixed decimation rate, DecimationFactor,
DifferentialDelay, and NumSections values of
8, 1, and 3, respectively, and GainCorrection set to
true. The System object returns valid output data at every eighth cycle based on the fixed DecimationFactor value of 8.
The latency of the object is 15 clock cycles and is calculated as 3 + N
+ 9.

This figure shows the output of the System object for variable R values of 2, 4, and 8 along with M and
N values of 1 and 3. The GainCorrection property
is set to false. The System object returns valid output data at the second, fourth, and eighth cycles
corresponding to the R values 2, 4, and 8, respectively. The
System object accepts R argument value changes only when the input
validIn is 1 (true). The
latency of the System object is 7 clock cycles, calculated as 4 + N.

This section shows the output of the System object for a vector input with different R, M, and N values.
This figure shows the output of the System object for a two-element column vector input with the default configuration, that
is, with a fixed decimation rate and DecimationFactor,
DifferentialDelay, and NumSections values of
2, 1, and 2, respectively. The latency of the object is 12 clock cycles.

This figure shows the output of the System object for an eight-element column vector input with a fixed decimation rate,
R, M, and N values of 8, 1, and
3, respectively, and GainCorrection set to true.
The latency of the object is 44 clock cycles.

The performance of the synthesized HDL code varies with your target and synthesis options. It also varies based on the input data type.
This table shows the resource and performance data synthesis results of the object for a
scalar input of type fixdt(1,16,0) with fixed and variable decimation
rates and for a two-element column vector input with fixed decimation rate
DecimationFactor, DifferentialDelay, and
NumSections values are 2, 1, and 2, respectively. The generated HDL
is targeted to the AMD®
Zynq®-7000 ZC706 Evaluation Board.
| Input Data | Decimation Type | Slice LUTs | Slice Registers | Maximum Frequency in MHz |
|---|---|---|---|---|
| Scalar | Fixed rate | 101 | 166 | 711.74 |
| Variable rate | 206 | 186 | 441.70 | |
| Vector | Fixed rate | 218 | 627 | 624.61 |
The resources and frequencies vary based on the type of input data and the values of R, M, and N, as well as other properties. Using a vector input can increase the throughput, however, doing so also increases the number of hardware resources that the System object uses.
References
[1] Hogenauer, E. “An Economical Class of Digital Filters for Decimation and Interpolation.” IEEE Transactions on Acoustics, Speech, and Signal Processing 29, no. 2 (April 1981): 155–62. https://doi.org/10.1109/TASSP.1981.1163535.
Extended Capabilities
This System object supports C/C++ code generation for accelerating MATLAB simulations, and for DPI component generation.
The software supports double and
single data types for simulation, but not for HDL code generation.
To generate HDL code from predefined System objects, see Generate HDL Code for IIR Filter.
Version History
Introduced in R2019bBefore R2022a, this System object was named dsp.HDLCICDecimation and was included in the
DSP System Toolbox™.
You can now set the decimation factor to
1. In previous releases, a decimation factor of1was invalid.The
ResetInproperty is renamed toResetInputPort.
| Configuration | Before R2022a | After 2022a |
|---|---|---|
| Variable decimation factor | Select the VariableDownsample property and set the
DecimationFactor parameter to the maximum expected decimation
factor. | Set the DecimationSource property to 'Input
port' and set the MaxDecimationFactor property to
the maximum expected decimation factor. The decimFactor
argument is renamed to R. |
| Fixed decimation factor | Clear the VariableDownsample property and set the
DecimationFactor property to the desired decimation
factor. | Set the DecimationSource property to
'Property' and set the DecimationFactor
property to the desired decimation factor. |
The object accepts and returns a column vector of elements that represent samples in time. The input vector can contain up to 64 samples. When you use frame-based input, you must use a fixed decimation factor.
You can optionally enable automatic gain correction. You can also specify the decimation factor as an input argument.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)