perfcurve
Receiver operating characteristic (ROC) curve or other performance curve for classifier output
Syntax
Description
[___] = perfcurve( returns
the coordinates of a ROC curve and any other output argument from
the previous syntaxes, with additional options specified by one or
more labels,scores,posclass,Name,Value)Name,Value pair arguments.
For example, you can provide a list of negative classes, change
the X or Y criterion, compute pointwise confidence
bounds using cross validation or bootstrap, specify the misclassification
cost, or compute the confidence bounds in parallel.
Examples
Load the sample data.
load fisheririsUse only the first two features as predictor variables. Define a binary classification problem by using only the measurements that correspond to the species versicolor and virginica.
pred = meas(51:end,1:2);
Define the binary response variable.
resp = (1:100)'>50; % Versicolor = 0, virginica = 1Fit a logistic regression model.
mdl = fitglm(pred,resp,'Distribution','binomial','Link','logit');
Compute the ROC curve. Use the probability estimates from the logistic regression model as scores.
scores = mdl.Fitted.Probability;
[X,Y,T,AUC] = perfcurve(species(51:end,:),scores,'virginica');perfcurve stores the threshold values in the array T.
Display the area under the curve.
AUC
AUC = 0.7918
The area under the curve is 0.7918. The maximum AUC is 1, which corresponds to a perfect classifier. Larger AUC values indicate better classifier performance.
Plot the ROC curve.
plot(X,Y) xlabel('False positive rate') ylabel('True positive rate') title('ROC for Classification by Logistic Regression')

Alternatively, you can compute and plot the ROC curve by creating a rocmetrics object and using the object function plot.
rocObj = rocmetrics(species(51:end,:),scores,'virginica');
plot(rocObj)
The plot function displays a filled circle at the model operating point, and the legend displays the class name and AUC value for the curve.
Load the sample data.
load ionosphereX is a 351x34 real-valued matrix of predictors. Y is a character array of class labels: 'b' for bad radar returns and 'g' for good radar returns.
Reformat the response to fit a logistic regression. Use the predictor variables 3 through 34.
resp = strcmp(Y,'b'); % resp = 1, if Y = 'b', or 0 if Y = 'g' pred = X(:,3:34);
Fit a logistic regression model to estimate the posterior probabilities for a radar return to be a bad one.
mdl = fitglm(pred,resp,'Distribution','binomial','Link','logit'); score_log = mdl.Fitted.Probability; % Probability estimates
Compute the standard ROC curve using the probabilities for scores.
[Xlog,Ylog,Tlog,AUClog] = perfcurve(resp,score_log,'true');Train an SVM classifier on the same sample data. Standardize the data.
mdlSVM = fitcsvm(pred,resp,'Standardize',true);Compute the posterior probabilities (scores).
mdlSVM = fitPosterior(mdlSVM); [~,score_svm] = resubPredict(mdlSVM);
The second column of score_svm contains the posterior probabilities of bad radar returns.
Compute the standard ROC curve using the scores from the SVM model.
[Xsvm,Ysvm,Tsvm,AUCsvm] = perfcurve(resp,score_svm(:,mdlSVM.ClassNames),'true');Fit a naive Bayes classifier on the same sample data.
mdlNB = fitcnb(pred,resp);
Compute the posterior probabilities (scores).
[~,score_nb] = resubPredict(mdlNB);
Compute the standard ROC curve using the scores from the naive Bayes classification.
[Xnb,Ynb,Tnb,AUCnb] = perfcurve(resp,score_nb(:,mdlNB.ClassNames),'true');Plot the ROC curves on the same graph.
plot(Xlog,Ylog) hold on plot(Xsvm,Ysvm) plot(Xnb,Ynb) legend('Logistic Regression','Support Vector Machines','Naive Bayes','Location','Best') xlabel('False positive rate'); ylabel('True positive rate'); title('ROC Curves for Logistic Regression, SVM, and Naive Bayes Classification') hold off

Although SVM produces better ROC values for higher thresholds, logistic regression is usually better at distinguishing the bad radar returns from the good ones. The ROC curve for naive Bayes is generally lower than the other two ROC curves, which indicates worse in-sample performance than the other two classifier methods.
Compare the area under the curve for all three classifiers.
AUClog
AUClog = 0.9659
AUCsvm
AUCsvm = 0.9489
AUCnb
AUCnb = 0.9393
Logistic regression has the highest AUC measure for classification and naive Bayes has the lowest. This result suggests that logistic regression has better in-sample average performance for this sample data.
This example shows how to determine the better parameter value for a custom kernel function in a classifier using the ROC curves.
Generate a random set of points within the unit circle.
rng(1); % For reproducibility n = 100; % Number of points per quadrant r1 = sqrt(rand(2*n,1)); % Random radii t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3 X1 = [r1.*cos(t1) r1.*sin(t1)]; % Polar-to-Cartesian conversion r2 = sqrt(rand(2*n,1)); t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4 X2 = [r2.*cos(t2) r2.*sin(t2)];
Define the predictor variables. Label points in the first and third quadrants as belonging to the positive class, and those in the second and fourth quadrants in the negative class.
pred = [X1; X2];
resp = ones(4*n,1);
resp(2*n + 1:end) = -1; % Labels
Create the function mysigmoid.m , which accepts two matrices in the feature space as inputs, and transforms them into a Gram matrix using the sigmoid kernel.
function G = mysigmoid(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 1; c = -1; G = tanh(gamma*U*V' + c); end
Train an SVM classifier using the sigmoid kernel function. It is good practice to standardize the data.
SVMModel1 = fitcsvm(pred,resp,'KernelFunction','mysigmoid',... 'Standardize',true); SVMModel1 = fitPosterior(SVMModel1); [~,scores1] = resubPredict(SVMModel1);
Set gamma = 0.5 ; within mysigmoid.m and save as mysigmoid2.m. And, train an SVM classifier using the adjusted sigmoid kernel.
function G = mysigmoid2(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 0.5; c = -1; G = tanh(gamma*U*V' + c); end
SVMModel2 = fitcsvm(pred,resp,'KernelFunction','mysigmoid2',... 'Standardize',true); SVMModel2 = fitPosterior(SVMModel2); [~,scores2] = resubPredict(SVMModel2);
Compute the ROC curves and the area under the curve (AUC) for both models.
[x1,y1,~,auc1] = perfcurve(resp,scores1(:,2),1); [x2,y2,~,auc2] = perfcurve(resp,scores2(:,2),1);
Plot the ROC curves.
plot(x1,y1) hold on plot(x2,y2) hold off legend('gamma = 1','gamma = 0.5','Location','SE'); xlabel('False positive rate'); ylabel('True positive rate'); title('ROC for classification by SVM');

The kernel function with the gamma parameter set to 0.5 gives better in-sample results.
Compare the AUC measures.
auc1 auc2
auc1 =
0.9518
auc2 =
0.9985
The area under the curve for gamma set to 0.5 is higher than that for gamma set to 1. This also confirms that gamma parameter value of 0.5 produces better results. For visual comparison of the classification performance with these two gamma parameter values, see Train SVM Classifier Using Custom Kernel.
Load the sample data.
load fisheririsThe column vector, species, consists of iris flowers of three different species: setosa, versicolor, virginica. The double matrix meas consists of four types of measurements on the flowers: sepal length, sepal width, petal length, and petal width. All measures are in centimeters.
Train a classification tree using the sepal length and width as the predictor variables. It is a good practice to specify the class names.
Model = fitctree(meas(:,1:2),species, ... 'ClassNames',{'setosa','versicolor','virginica'});
Predict the class labels and scores for the species based on the tree Model.
[~,score] = resubPredict(Model);
The scores are the posterior probabilities that an observation (a row in the data matrix) belongs to a class. The columns of score correspond to the classes specified by 'ClassNames'. So, the first column corresponds to setosa, the second corresponds to versicolor, and the third column corresponds to virginica.
Compute the ROC curve for the predictions that an observation belongs to versicolor, given the true class labels species. Also compute the optimal operating point and y values for negative subclasses. Return the names of the negative classes.
Because this is a multiclass problem, you cannot merely supply score(:,2) as input to perfcurve. Doing so would not give perfcurve enough information about the scores for the two negative classes (setosa and virginica). This problem is unlike a binary classification problem, where knowing the scores of one class is enough to determine the scores of the other class. Therefore, you must supply perfcurve with a function that factors in the scores of the two negative classes. One such function is , which corresponds to the one-versus-all coding design.
diffscore1 = score(:,2) - max(score(:,1),score(:,3));
The values in diffscore are classification scores for a binary problem that treats the second class as a positive class and the rest as negative classes.
[X,Y,T,~,OPTROCPT,suby,subnames] = perfcurve(species,diffscore1,'versicolor');X, by default, is the false positive rate (fallout or 1-specificity) and Y, by default, is the true positive rate (recall or sensitivity). The positive class label is versicolor. Because a negative class is not defined, perfcurve assumes that the observations that do not belong to the positive class are in one class. The function accepts it as the negative class.
OPTROCPT
OPTROCPT = 1×2
0.1000 0.8000
suby
suby = 12×2
0 0
0.1800 0.1800
0.4800 0.4800
0.5800 0.5800
0.6200 0.6200
0.8000 0.8000
0.8800 0.8800
0.9200 0.9200
0.9600 0.9600
0.9800 0.9800
1.0000 1.0000
1.0000 1.0000
⋮
subnames
subnames = 1×2 cell
{'setosa'} {'virginica'}
Plot the ROC curve and the optimal operating point on the ROC curve.
plot(X,Y) hold on plot(OPTROCPT(1),OPTROCPT(2),'ro') xlabel('False positive rate') ylabel('True positive rate') title('ROC Curve for Classification by Classification Trees') hold off

Find the threshold that corresponds to the optimal operating point.
T((X==OPTROCPT(1))&(Y==OPTROCPT(2)))
ans = 0.2857
Specify virginica as the negative class and compute and plot the ROC curve for versicolor.
Again, you must supply perfcurve with a function that factors in the scores of the negative class. An example of a function to use is .
diffscore2 = score(:,2) - score(:,3); [X,Y,~,~,OPTROCPT] = perfcurve(species,diffscore2,'versicolor', ... 'negClass','virginica'); OPTROCPT
OPTROCPT = 1×2
0.1800 0.8200
figure, plot(X,Y) hold on plot(OPTROCPT(1),OPTROCPT(2),'ro') xlabel('False positive rate') ylabel('True positive rate') title('ROC Curve for Classification by Classification Trees') hold off

Alternatively, you can use a rocmetrics object to create the ROC curve. rocmetrics supports multiclass classification problems using the one-versus-all coding design, which reduces a multiclass problem into a set of binary problems. You can examine the performance of a multiclass problem on each class by plotting a one-versus-all ROC curve for each class.
Compute the performance metrics by creating a rocmetrics object. Specify the true labels, classification scores, and class names.
rocObj = rocmetrics(species,score,Model.ClassNames);
Plot the ROC curve for each class by using the plot function of rocmetrics.
figure plot(rocObj)

The plot function displays a filled circle at the model operating point for each class, and the legend shows the class name and AUC value for each curve. You can find the optimal operating points by using the properties stored in the rocmetrics object rocObj. For an example, see Find Model Operating Point and Optimal Operating Point.
Load the sample data.
load fisheririsThe column vector species consists of iris flowers of three different species: setosa, versicolor, virginica. The double matrix meas consists of four types of measurements on the flowers: sepal length, sepal width, petal length, and petal width. All measures are in centimeters.
Use only the first two features as predictor variables. Define a binary problem by using only the measurements that correspond to the versicolor and virginica species.
pred = meas(51:end,1:2);
Define the binary response variable.
resp = (1:100)'>50; % Versicolor = 0, virginica = 1Fit a logistic regression model.
mdl = fitglm(pred,resp,'Distribution','binomial','Link','logit');
Compute the pointwise confidence intervals on the true positive rate (TPR) by vertical averaging (VA) and sampling using bootstrap.
[X,Y,T] = perfcurve(species(51:end,:),mdl.Fitted.Probability,... 'virginica','NBoot',1000,'XVals',[0:0.05:1]);
'NBoot',1000 sets the number of bootstrap replicas to 1000. 'XVals','All' prompts perfcurve to return X, Y, and T values for all scores, and average the Y values (true positive rate) at all X values (false positive rate) using vertical averaging. If you do not specify XVals, then perfcurve computes the confidence bounds using threshold averaging by default.
Plot the pointwise confidence intervals.
errorbar(X,Y(:,1),Y(:,1)-Y(:,2),Y(:,3)-Y(:,1)); xlim([-0.02,1.02]); ylim([-0.02,1.02]); xlabel('False positive rate') ylabel('True positive rate') title('ROC Curve with Pointwise Confidence Bounds') legend('PCBwVA','Location','Best')

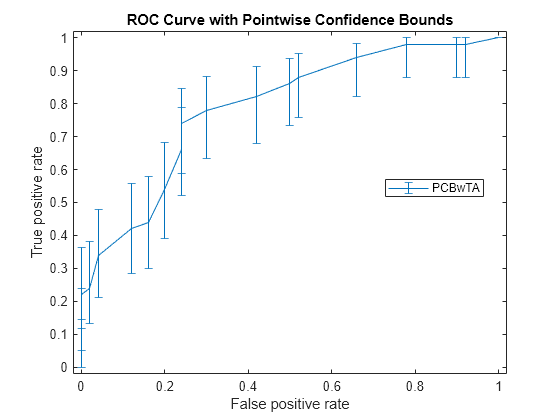
It might not always be possible to control the false positive rate (FPR, the X value in this example). So you might want to compute the pointwise confidence intervals on true positive rates (TPR) by threshold averaging.
[X1,Y1,T1] = perfcurve(species(51:end,:),mdl.Fitted.Probability,... 'virginica','NBoot',1000);
If you set 'TVals' to 'All', or if you do not specify 'TVals' or 'Xvals', then perfcurve returns X, Y, and T values for all scores and computes pointwise confidence bounds for X and Y using threshold averaging.
Plot the confidence bounds.
figure() errorbar(X1(:,1),Y1(:,1),Y1(:,1)-Y1(:,2),Y1(:,3)-Y1(:,1)); xlim([-0.02,1.02]); ylim([-0.02,1.02]); xlabel('False positive rate') ylabel('True positive rate') title('ROC Curve with Pointwise Confidence Bounds') legend('PCBwTA','Location','Best')

Specify the threshold values to fix and compute the ROC curve. Then plot the curve.
[X1,Y1,T1] = perfcurve(species(51:end,:),mdl.Fitted.Probability,... 'virginica','NBoot',1000,'TVals',0:0.05:1); figure() errorbar(X1(:,1),Y1(:,1),Y1(:,1)-Y1(:,2),Y1(:,3)-Y1(:,1)); xlim([-0.02,1.02]); ylim([-0.02,1.02]); xlabel('False positive rate') ylabel('True positive rate') title('ROC Curve with Pointwise Confidence Bounds') legend('PCBwTA','Location','Best')
Input Arguments
True class labels, specified as a numeric vector, logical vector, character matrix, string
array, categorical array, cell array of character vectors, or cell array. If
labels is a cell array, it can contain elements with one of the other
types. In this case, perfcurve uses cross-validation and treats each
element of the cell array as a cross-validation fold. If scores is a cell
array, labels must also be a cell array. labels and
scores must contain the same number of elements. For more information,
see Grouping Variables.
Example: {"hi","mid","hi","low",...,"mid"}
Example: ["H","M","H","L",...,"M"]
Data Types: single | double | logical | char | string | cell | categorical
Scores returned by a classifier for sample data, specified as a vector or cell array of
floating points. scores must contain the same number of elements as
labels. If labels is a cell array representing
cross-validation folds, scores must also be a cell array.
Example: [0.82;0.60;0.79;0.16;…;0.71;0.48;0.63;0.53;0.35]
Data Types: single | double | cell
Positive class label, specified as a numeric scalar, logical scalar, character vector, string
scalar, cell containing a character vector, or categorical scalar. The positive class must be
a member of the input labels. The value of posclass that you can specify
depends on the value of labels.
labels value | posclass value |
|---|---|
| Numeric vector | Numeric scalar |
| Logical vector | Logical scalar |
| Character matrix | Character vector |
| String array | String scalar |
| Cell array of character vectors | Character vector or cell containing character vector |
| Categorical vector | Categorical scalar |
For example, in a cancer diagnosis problem, if a malignant tumor
is the positive class, then specify posclass as 'malignant'.
Data Types: single | double | logical | char | string | cell | categorical
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'NegClass','versicolor','XCrit','fn','NBoot',1000,'BootType','per' specifies
the species versicolor as the negative class, the criterion for the
X-coordinate as false negative, the number of bootstrap samples as
1000. It also specifies that the pointwise confidence bounds are computed
using the percentile method.
List of negative classes, specified as the comma-separated pair consisting of
'NegClass', and a numeric array, a categorical array, a string array, or
a cell array of character vectors. By default, perfcurve sets
NegClass to 'all' and considers all nonpositive
classes found in the input array of labels to be negative.
If NegClass is a subset of the classes
found in the input array of labels, then perfcurve discards
the instances with labels that do not belong to either positive or
negative classes.
Example: 'NegClass',{'versicolor','setosa'}
Data Types: single | double | categorical | char | string | cell
Criterion to compute for X, specified as
the comma-separated pair consisting of 'XCrit' and
one of the following.
| Criterion | Description |
|---|---|
tp | Number of true positive instances. |
fn | Number of false negative instances. |
fp | Number of false positive instances. |
tn | Number of true negative instances. |
tp+fp | Sum of true positive and false positive instances. |
rpp | Rate of positive predictions.rpp =
(tp+fp)/(tp+fn+fp+tn) |
rnp | Rate of negative predictions. rnp
= (tn+fn)/(tp+fn+fp+tn) |
accu | Accuracy. accu = (tp+tn)/(tp+fn+fp+tn) |
tpr, or sens, or reca | True positive rate, or sensitivity, or recall. tpr=
sens = reca = tp/(tp+fn) |
fnr, or miss | False negative rate, or miss. fnr
= miss = fn/(tp+fn) |
fpr, or fall | False positive rate, or fallout, or 1 – specificity. fpr = fall = fp/(tn+fp) |
tnr, or spec | True negative rate, or specificity. tnr
= spec = tn/(tn+fp) |
ppv, or prec | Positive predictive value, or precision. ppv
= prec = tp/(tp+fp) |
npv | Negative predictive value. npv = tn/(tn+fn) |
ecost | Expected cost. ecost = (tp*Cost(P|P)+fn*Cost(N|P)+fp*
Cost(P|N)+tn*Cost(N|N))/(tp+fn+fp+tn) |
| Custom criterion | A custom-defined function with the input arguments (C,scale,cost),
where C is a 2-by-2 confusion matrix, scale is
a 2-by-1 array of class scales, and cost is a 2-by-2
misclassification cost matrix. |
Caution
Some of these criteria return NaN values
at one of the two special thresholds, 'reject all' and 'accept
all'.
Example: 'XCrit','ecost'
Values for the X criterion, specified as
the comma-separated pair consisting of 'XVals' and
a numeric array.
If you specify
XVals, thenperfcurvecomputesXandYand the pointwise confidence bounds forY(when applicable) only for the specifiedXVals.If you do not specify
XVals, thenperfcurve, computesXandYand the values for all scores by default.
Note
You cannot set XVals and TVals at
the same time.
Example: 'XVals',[0:0.05:1]
Data Types: single | double | char | string
Thresholds for the positive class score, specified as the comma-separated
pair consisting of 'TVals' and either 'all' or
a numeric array.
If
TValsis set to'all'or not specified, andXValsis not specified, thenperfcurvereturnsX,Y, andTvalues for all scores and computes pointwise confidence bounds forXandYusing threshold averaging.If
TValsis set to a numeric array, thenperfcurvereturnsX,Y, andTvalues for the specified thresholds and computes pointwise confidence bounds forXandYat these thresholds using threshold averaging.
Note
You cannot set XVals and TVals at
the same time.
Example: 'TVals',[0:0.05:1]
Data Types: single | double | char | string
Indicator to use the nearest values in the data instead of the specified numeric
XVals or TVals, specified as the comma-separated pair
consisting of 'UseNearest' and either 'on' or
'off'.
If you specify numeric
XValsand setUseNearestto'on', thenperfcurvereturns the nearest uniqueXvalues found in the data, and it returns the corresponding values ofYandT.If you specify numeric
XValsand setUseNearestto'off', thenperfcurvereturns the sortedXVals.If you compute confidence bounds by cross validation or bootstrap, then this parameter is always
'off'.
Example: 'UseNearest','off'
perfcurve method for processing NaN scores,
specified as the comma-separated pair consisting of 'ProcessNaN' and 'ignore' or 'addtofalse'.
If
ProcessNaNis'ignore', thenperfcurveremoves observations withNaNscores from the data.If
ProcessNaNis'addtofalse', thenperfcurveadds instances withNaNscores to false classification counts in the respective class. That is,perfcurvealways counts instances from the positive class as false negative (FN), and it always counts instances from the negative class as false positive (FP).
Example: 'ProcessNaN','addtofalse'
Prior probabilities for positive and negative classes, specified
as the comma-separated pair consisting of 'Prior' and 'empirical', 'uniform',
or an array with two elements.
If Prior is 'empirical',
then perfcurve derives prior probabilities from
class frequencies.
If Prior is 'uniform' ,
then perfcurve sets all prior probabilities to
be equal.
Example: 'Prior',[0.3,0.7]
Data Types: single | double | char | string
Misclassification costs, specified as the comma-separated pair
consisting of 'Cost' and a 2-by-2 matrix, containing [Cost(P|P),Cost(N|P);Cost(P|N),Cost(N|N)].
Cost(N|P) is the cost of misclassifying a
positive class as a negative class. Cost(P|N) is
the cost of misclassifying a negative class as a positive class. Usually, Cost(P|P) =
0 and Cost(N|N) = 0, but perfcurve allows
you to specify nonzero costs for correct classification as well.
Example: 'Cost',[0 0.7;0.3 0]
Data Types: single | double
Significance level for the confidence bounds, specified as the comma-separated pair
consisting of 'Alpha' and a scalar value in the range 0 through 1.
perfcurve computes 100*(1 – α) percent pointwise confidence bounds for
X, Y, T, and
AUC for a confidence level of 1 – α.
Example: 'Alpha',0.01 specifies 99% confidence bounds.
Data Types: single | double
Observation weights, specified as the comma-separated pair consisting
of 'Weights' and a vector of nonnegative scalar
values. This vector must have as many elements as scores or labels do.
If scores and labels are
in cell arrays and you need to supply Weights,
the weights must be in a cell array as well. In this case, every element
in Weights must be a numeric vector with as many
elements as the corresponding element in scores.
For example, numel(weights{1}) == numel(scores{1}).
When perfcurve computes the X, Y and T or
confidence bounds using cross-validation, it uses these observation
weights instead of observation counts.
When perfcurve computes confidence bounds
using bootstrap, it samples N out of N observations
with replacement, using these weights as multinomial sampling probabilities.
The default is a vector of 1s or a cell array in which each element is a vector of 1s.
Data Types: single | double | cell
Number of bootstrap replicas for computation of confidence bounds,
specified as the comma-separated pair consisting of 'NBoot' and
a positive integer. The default value 0 means the confidence bounds
are not computed.
If labels and scores are
cell arrays, this parameter must be 0 because perfcurve can
use either cross-validation or bootstrap to compute confidence bounds.
Example: 'NBoot',500
Data Types: single | double
Confidence interval type for bootci to use to compute confidence intervals,
specified as the comma-separated pair consisting of 'BootType' and one of
the following:
'bca'— Bias corrected and accelerated percentile method'normor'normal'— Normal approximated interval with bootstrapped bias and standard error'per'or'percentile'— Percentile method'cper'or'corrected percentile'— Bias corrected percentile method'stud'or'student'— Studentized confidence interval
Example: 'BootType','cper'
Optional input arguments for bootci to compute confidence bounds, specified
as the comma-separated pair consisting of 'BootArg' and
{'Nbootstd',nbootstd}.
When you compute the studentized bootstrap confidence intervals ('BootType' is 'student'), you can additionally specify the
'Nbootstd' name-value pair argument of bootci by
using 'BootArg'. For example,
'BootArg',{'Nbootstd',nbootstd} estimates the standard error of the
bootstrap statistics using bootstrap with nbootstd data samples.
nbootstd is a positive integer and its default is 100.
Example: 'BootArg',{'Nbootstd',nbootstd}
Data Types: cell
Options for controlling the computation of confidence intervals, specified as the
comma-separated pair consisting of 'Options' and a structure array
returned by statset. These options require Parallel Computing Toolbox™. perfcurve uses this argument for computing pointwise
confidence bounds only. To compute these bounds, you must pass cell arrays for
labels and scores or set
NBoot to a positive integer.
This table summarizes the available options.
| Option | Description |
|---|---|
'UseParallel' |
|
'UseSubstreams' |
|
'Streams' | A
In that case, use a cell array of the same size as the
parallel pool. If a parallel pool is not open, then |
If 'UseParallel' is true and
'UseSubstreams' is false, then the length of
'Streams' must equal the number of workers used by
perfcurve. If a parallel pool is already open, then the length of
'Streams' is the size of the parallel pool. If a parallel pool is not
already open, then MATLAB® might open a pool for you, depending on your installation and settings. To
ensure more predictable results, use parpool (Parallel Computing Toolbox) and explicitly create a parallel pool before invoking
perfcurve and setting
'Options',statset('UseParallel',true).
Example: 'Options',statset('UseParallel',true)
Data Types: struct
Output Arguments
x-coordinates for the performance curve,
returned as a vector or an m-by-3 matrix. By default, X values
are the false positive rate, FPR (fallout or 1 – specificity).
To change X, use the XCrit name-value
pair argument.
If
perfcurvedoes not compute the pointwise confidence bounds, or if it computes them using vertical averaging, thenXis a vector.If
perfcurvecomputes the confidence bounds using threshold averaging, thenXis an m-by-3 matrix, where m is the number of fixed threshold values. The first column ofXcontains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the pointwise confidence bounds.
y-coordinates for the performance curve,
returned as a vector or an m-by-3 matrix. By default, Y values
are the true positive rate, TPR (recall or sensitivity). To change Y,
use YCrit name-value pair argument.
If
perfcurvedoes not compute the pointwise confidence bounds, thenYis a vector.If
perfcurvecomputes the confidence bounds, thenYis an m-by-3 matrix, where m is the number of fixedXvalues or thresholds (Tvalues). The first column ofYcontains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the pointwise confidence bounds.
Thresholds on classifier scores for the computed values of X and Y,
returned as a vector or m-by-3 matrix.
If
perfcurvedoes not compute the pointwise confidence bounds, or computes them using threshold averaging, thenTis a vector.If
perfcurvecomputes the confidence bounds using vertical averaging,Tis an m-by-3 matrix, where m is the number of fixedXvalues. The first column ofTcontains the mean value. The second and third columns contain the lower bound, and the upper bound, respectively, of the pointwise confidence bounds.
For each threshold, TP is the count of true
positive observations with scores greater than or equal to this threshold,
and FP is the count of false positive observations
with scores greater than or equal to this threshold. perfcurve defines
negative counts, TN and FN,
in a similar way. The function then sorts the thresholds in the descending
order that corresponds to the ascending order of positive counts.
For the m distinct thresholds found in the
array of scores, perfcurve returns the X, Y and T arrays
with m + 1 rows. perfcurve sets
elements T(2:m+1) to the distinct
thresholds, and T(1) replicates T(2).
By convention, T(1) represents the highest 'reject
all' threshold, and perfcurve computes
the corresponding values of X and Y for TP
= 0 and FP = 0. The T(end) value
is the lowest 'accept all' threshold for which TN
= 0 and FN = 0.
Area under the curve (AUC) for the computed
values of X and Y, returned
as a scalar value or a 3-by-1 vector.
If
perfcurvedoes not compute the pointwise confidence bounds,AUCis a scalar value.If
perfcurvecomputes the confidence bounds using vertical averaging,AUCis a 3-by-1 vector. The first column ofAUCcontains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the confidence bound.
For a perfect classifier, AUC = 1. For a classifier that randomly assigns observations to classes, AUC = 0.5.
If you set XVals to 'all' (default),
then perfcurve computes AUC using
the returned X and Y values.
If XVals is a numeric array, then perfcurve computes AUC using X and Y values
from all distinct scores in the interval, which are specified by the
smallest and largest elements of XVals. More
precisely, perfcurve finds X values
for all distinct thresholds as if XVals were
set to 'all', and then uses a subset of these (with
corresponding Y values) between min(XVals) and max(XVals) to
compute AUC.
perfcurve uses trapezoidal approximation
to estimate the area. If the first or last value of X or Y are NaNs,
then perfcurve removes them to allow calculation
of AUC. This takes care of criteria that produce NaNs
for the special 'reject all' or 'accept
all' thresholds, for example, positive predictive value
(PPV) or negative predictive value (NPV).
Optimal operating point of the ROC curve, returned as a 1-by-2 array with false positive rate (FPR) and true positive rate (TPR) values for the optimal ROC operating point.
perfcurve computes OPTROCPT for
the standard ROC curve only, and sets to NaNs otherwise.
To obtain the optimal operating point for the ROC curve, perfcurve first
finds the slope, S, using
Cost(N|P) is the cost of misclassifying a positive class as a negative class. Cost(P|N) is the cost of misclassifying a negative class as a positive class.
P = TP + FN and N = TN + FP. They are the total instance counts in the positive and negative class, respectively.
perfcurve then finds the optimal
operating point by moving the straight line with slope S from
the upper left corner of the ROC plot (FPR = 0, TPR
= 1) down and to the right, until it intersects the ROC
curve.
Values for negative subclasses, returned as an array.
If you specify only one negative class, then
SUBYis identical toY.If you specify k negative classes, then
SUBYis a matrix of size m-by-k, where m is the number of returned values forXandY, and k is the number of negative classes.perfcurvecomputesYvalues by summing counts over all negative classes.
SUBY gives values of the Y criterion
for each negative class separately. For each negative class, perfcurve places
a new column in SUBY and fills it with Y values
for true negative (TN) and false positive (FP) counted just for this
class.
Negative class names, returned as a cell array.
If you provide an input array of negative class names
NegClass, thenperfcurvecopies names intoSUBYNAMES.If you do not provide
NegClass, thenperfcurveextractsSUBYNAMESfrom the input labels. The order ofSUBYNAMESis the same as the order of columns inSUBY. That is,SUBY(:,1)is for negative classSUBYNAMES{1},SUBY(:,2)is for negative classSUBYNAMES{2}, and so on.
Algorithms
If you supply cell arrays for labels and scores,
or if you set NBoot to a positive integer, then perfcurve returns
pointwise confidence bounds for X,Y,T,
and AUC. You cannot supply cell arrays for labels and scores and
set NBoot to a positive integer at the same time.
perfcurve resamples data to compute confidence
bounds using either cross validation or bootstrap.
Cross-validation — If you supply cell arrays for
labelsandscores, thenperfcurveuses cross-validation and treats elements in the cell arrays as cross-validation folds.labelscan be a cell array of numeric vectors, logical vectors, character matrices, cell arrays of character vectors, or categorical vectors. All elements inlabelsmust have the same type.scorescan be a cell array of numeric vectors. The cell arrays forlabelsandscoresmust have the same number of elements. The number of labels in cell j oflabelsmust be equal to the number of scores in cell j ofscoresfor any j in the range from 1 to the number of elements inscores.Bootstrap — If you set
NBootto a positive integer n,perfcurvegenerates n bootstrap replicas to compute pointwise confidence bounds. If you useXCritorYCritto set the criterion forXorYto an anonymous function,perfcurvecan compute confidence bounds only using bootstrap.
perfcurve estimates the confidence bounds
using one of two methods:
Vertical averaging (VA) —
perfcurveestimates confidence bounds onYandTat fixed values ofX. That is,perfcurvetakes samples of the ROC curves for fixedXvalues, averages the correspondingYandTvalues, and computes the standard errors. You can use theXValsname-value pair argument to fix theXvalues for computing confidence bounds. If you do not specifyXVals, thenperfcurvecomputes the confidence bounds at allXvalues.Threshold averaging (TA) —
perfcurvetakes samples of the ROC curves at fixed thresholdsTfor the positive class score, averages the correspondingXandYvalues, and estimates the confidence bounds. You can use theTValsname-value pair argument to use this method for computing confidence bounds. If you setTValsto'all'or do not specifyTValsorXVals, thenperfcurvereturnsX,Y, andTvalues for all scores and computes pointwise confidence bounds forYandXusing threshold averaging.
When you compute the confidence bounds, Y is
an m-by-3 array, where m is
the number of fixed X values or thresholds (T values).
The first column of Y contains the mean value.
The second and third columns contain the lower bound and the upper
bound, respectively, of the pointwise confidence bounds. AUC is
a row vector with three elements, following the same convention. If perfcurve computes
the confidence bounds using VA, then T is an m-by-3
matrix, and X is a column vector. If perfcurve uses
TA, then X is an m-by-3 matrix
and T is a column-vector.
perfcurve returns pointwise confidence
bounds. It does not return a simultaneous confidence band for the
entire curve.
Alternative Functionality
You can compute the performance metrics for a ROC curve and other performance curves by creating a
rocmetricsobject.rocmetricssupports both binary and multiclass classification problems. You can pass classification scores returned by thepredictfunction of a classification model object (such aspredictofClassificationTree) torocmetricswithout adjusting scores for a multiclass model.rocmetricsprovides object functions to plot a ROC curve (plot), find an average ROC curve for multiclass problems (average), and compute additional metrics after creating an object (addMetrics). For more details, see the reference pages and ROC Curve and Performance Metrics.
References
[1] Fawcett, T. “ROC Graphs: Notes and Practical Considerations for Researchers”, Machine Learning 31, no. 1 (2004): 1–38.
[2] Zweig, M., and G. Campbell. “Receiver-Operating Characteristic (ROC) Plots: A Fundamental Evaluation Tool in Clinical Medicine.” Clinical Chemistry 39, no. 4 (1993): 561–577.
[3] Davis, J., and M. Goadrich. “The Relationship Between Precision-Recall and ROC Curves.” Proceedings of ICML ’06, 2006, pp. 233–240.
[4] Moskowitz, C. S., and M. S. Pepe. “Quantifying and Comparing the Predictive Accuracy of Continuous Prognostic Factors for Binary Outcomes.” Biostatistics 5, no. 1 (2004): 113–27.
[5] Huang, Y., M. S. Pepe, and Z. Feng. “Evaluating the Predictiveness of a Continuous Marker.” U. Washington Biostatistics Paper Series, 2006, 250–61.
[6] Briggs, W. M., and R. Zaretzki. “The Skill Plot: A Graphical Technique for Evaluating Continuous Diagnostic Tests.” Biometrics 64, no. 1 (2008): 250–256.
[7] Bettinger, R. “Cost-Sensitive Classifier Selection Using the ROC Convex Hull Method.” SAS Institute, 2003.
Extended Capabilities
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2009aStarting in R2022a, the default value for the Cost name-value argument
is [0 1; 1 0], which is the same as the default misclassification cost matrix
value for the new feature rocmetrics and the classifier training functions,
such as fitcsvm, fitctree, and so on. In previous
releases, the default Cost value is [0 0.5; 0.5
0].
If you specify the XCrit or YCrit name-value
argument as 'ecost' (expected cost) and use the default
Cost value, the function returns values in the output argument
X or Y that are doubled compared to the values in
previous releases.
If you specify the XCrit or YCrit name-value
argument as a custom metric and use the default Cost value, the
corresponding output argument value can be different depending on how the custom metric uses a
cost matrix.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)