classify
Classify observations using discriminant analysis
Syntax
Description
Note
fitcdiscr and predict are recommended over classify for training a
discriminant analysis classifier and predicting labels. fitcdiscr
supports cross-validation and hyperparameter optimization, and does not require you to
fit the classifier every time you make a new prediction or change prior
probabilities.
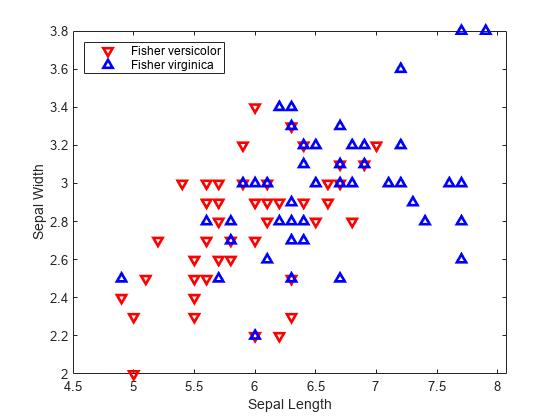
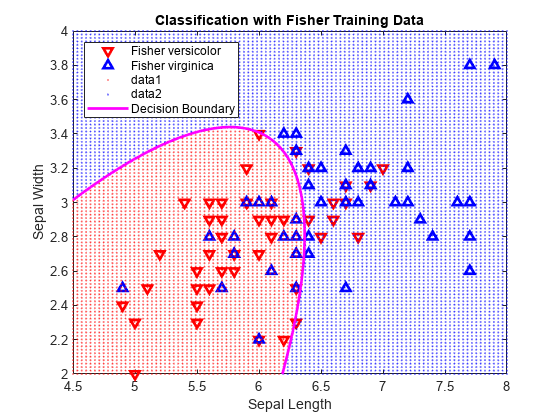
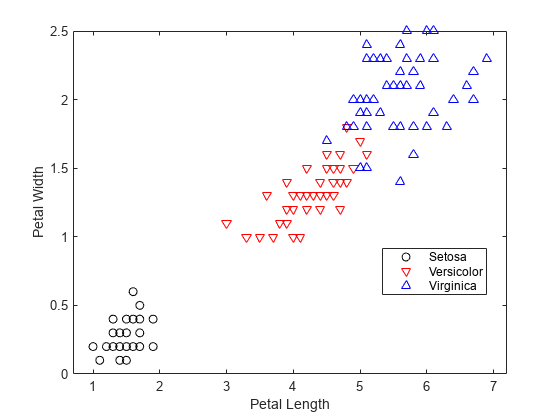
class = classify(sample,training,group)sample into one of the groups to
which the data in training belongs. The groups for
training are specified by group. The function
returns class, which contains the assigned groups for each row of
sample.
[
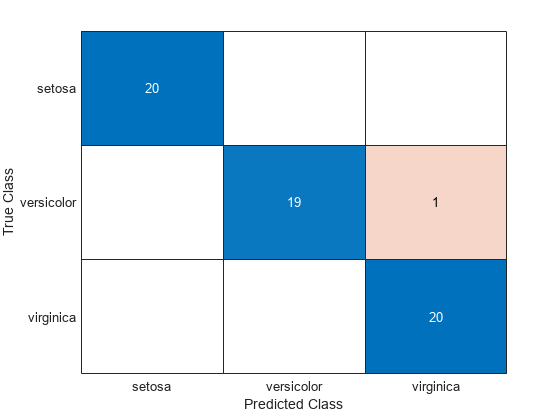
also returns the apparent error rate (class,err,posterior,logp,coeff] = classify(___)err), posterior probabilities for
training observations (posterior), logarithm of the unconditional
probability density for sample observations (logp), and coefficients of
the boundary curves (coeff), using any of the input argument
combinations in previous syntaxes.
Examples
Input Arguments
Output Arguments
Alternative Functionality
The fitcdiscr function also performs discriminant
analysis. You can train a classifier by using the fitcdiscr function and
predict labels of new data by using the predict function. The fitcdiscr function supports
cross-validation and hyperparameter optimization, and does not require you to fit the
classifier every time you make a new prediction or change prior probabilities.
References
[1] Krzanowski, Wojtek. J. Principles of Multivariate Analysis: A User's Perspective. NY: Oxford University Press, 1988.
[2] Seber, George A. F. Multivariate Observations. NJ: John Wiley & Sons, Inc., 1984.
Version History
Introduced before R2006a