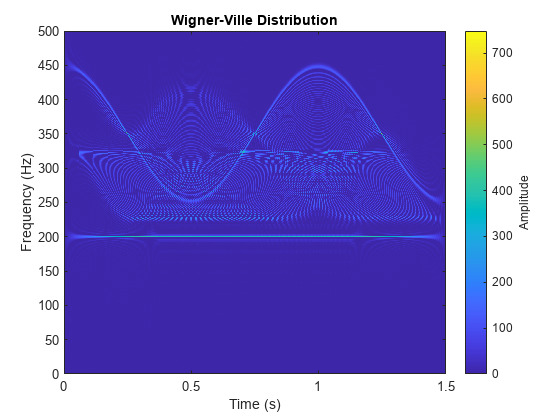
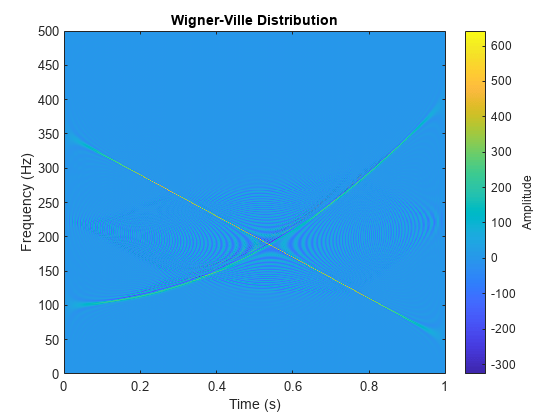
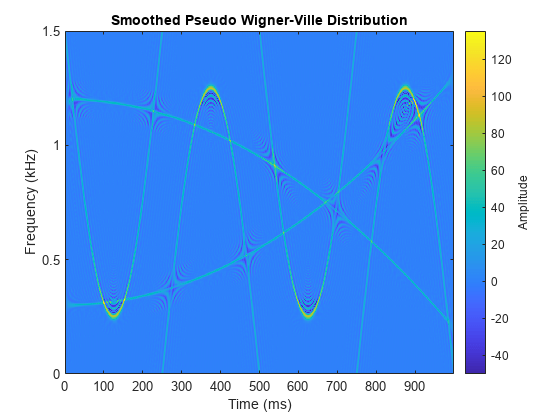
wvd
Wigner-Ville distribution and smoothed pseudo Wigner-Ville distribution
Syntax
Description
d = wvd(___,"smoothedPseudo",Name=Value)twin and
fwin in this syntax, or you can omit them.
wvd(___) with no output arguments plots the
Wigner-Ville or smoothed pseudo Wigner-Ville distribution in the current figure.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Cohen, Leon. Time-Frequency Analysis: Theory and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1995.
[2] Mallat, Stéphane. A Wavelet Tour of Signal Processing. Second Edition. San Diego, CA: Academic Press, 1999.
[3] O'Toole, John M., and Boualem Boashash. "Fast and Memory-Efficient algorithms for Computing Quadratic Time-Frequency Distributions." Applied and Computational Harmonic Analysis. Vol. 35, Number 2, 2013, pp. 350–358.