This example shows that the Fourier Synchrosqueezed Transform, despite the sharp ridges it produces, cannot resolve arbitrarily spaced sinusoids. The width of the window used by the transform dictates how closely spaced two sinusoids can be and still be detected as distinct.
Consider a sinusoid, , windowed with a Gaussian window, . The short-time transform is
When viewed as a function of frequency, the transform combines a constant (in time) oscillation at with Gaussian decay away from it. The synchrosqueezing estimate of the instantaneous frequency,
equals the value obtained by using the standard definition,
For a superposition of sinusoids,
the short-time transform becomes
Create 1024 samples of a signal consisting of two sinusoids. One sinusoid has a normalized frequency of rad/sample. The other sinusoid has three times the frequency and three times the amplitude.
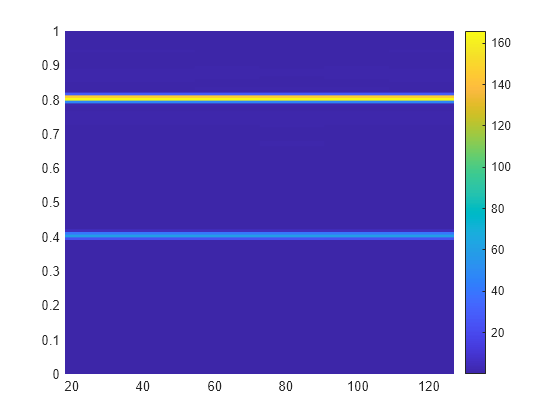
Use the spectrogram function to compute the short-time Fourier transform of the signal. Use a 256-sample Gaussian window with , 255 samples of overlap between adjoining sections, and 1024 DFT points. Plot the absolute value of the transform.
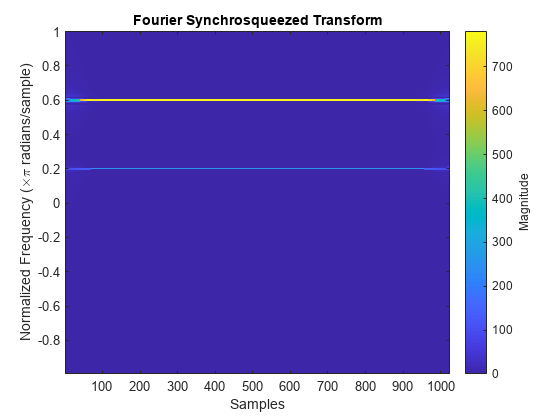
The Fourier synchrosqueezed transform, implemented in the fsst function, results in a sharper, better localized estimate of the spectrum.
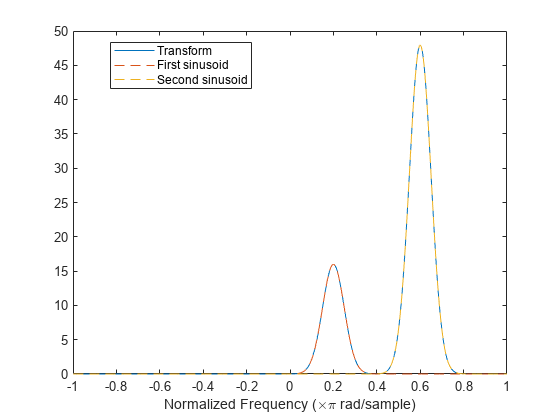
The sinusoids are visible as constant oscillations at the expected frequency values. To see that the decay away from the ridges is Gaussian, plot an instantaneous value of the transform and overlay two instances of a Gaussian. Express the Gaussian amplitude and standard deviation in terms of and the window length. Recall that the standard deviation of the frequency-domain window is the reciprocal of the standard deviation of the time-domain window.
The Fourier synchrosqueezed transform concentrates the energy content of the signal at the estimated instantaneous frequencies.
The synchrosqueezed estimates of instantaneous frequency are valid only if the sinusoids are separated by more than , where
for a Gaussian window and is the standard deviation.
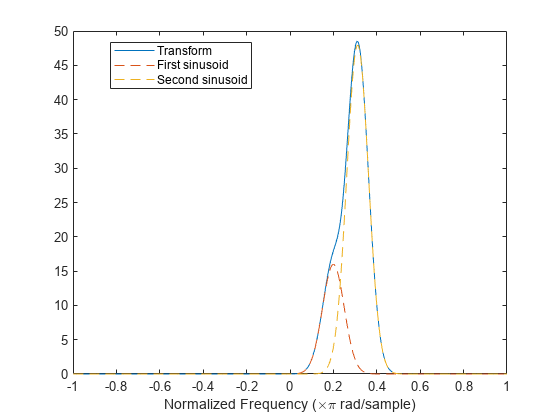
Repeat the previous calculation, but now specify that the second sinusoid has a normalized frequency of rad/sample.
The Fourier synchrosqueezed transform cannot resolve the sinusoids well because . The spectral estimates decrease significantly in value.