stft

Short-time Fourier transform

Syntax

s = stft(x)

s = stft(x,fs)

s = stft(x,ts)

s = stft(___,Name=Value)

[s,f] = stft(___)

[s,f,t] = stft(___)

stft(___)

Description

s = stft(x) returns the Short-Time Fourier Transform (STFT) of x.

s = stft(x,fs) returns the STFT of x using sample rate fs.

s = stft(x,ts) returns the STFT of x using sample time ts.

s = stft(___,Name=Value) specifies additional options using name-value arguments. Options include the FFT window and length. These arguments can be added to any of the previous input syntaxes.

[s,f] = stft(___) returns the frequencies f at which the STFT is evaluated.

[s,f,t] = stft(___) returns the times at which the STFT is evaluated.

stft(___) with no output arguments plots the magnitude squared of the STFT in decibels in the current figure window.

Examples

Short-Time Fourier Transform

Generate a chirp with sinusoidally varying frequency. The signal is sampled at 10 kHz for two seconds.

fs = 10e3;
t = 0:1/fs:2;
x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);

Compute the short-time Fourier transform of the chirp. Divide the signal into 256-sample segments and window each segment using a Kaiser window with shape parameter β = 5. Specify 220 samples of overlap between adjoining segments and a DFT length of 512. Output the frequency and time values at which the STFT is computed.

[s,f,t] = stft(x,fs,Window=kaiser(256,5),OverlapLength=220,FFTLength=512);

The magnitude squared of the STFT is also known as the spectrogram. Plot the spectrogram in decibels. Specify a colormap that spans 60 dB and whose last color corresponds to the maximum value of the spectrogram.

sdb = mag2db(abs(s));
mesh(t,f/1000,sdb);

cc = max(sdb(:))+[-60 0];
ax = gca;
ax.CLim = cc;
view(2)
colorbar

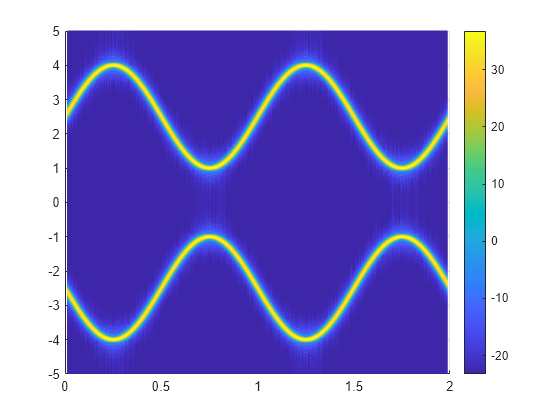
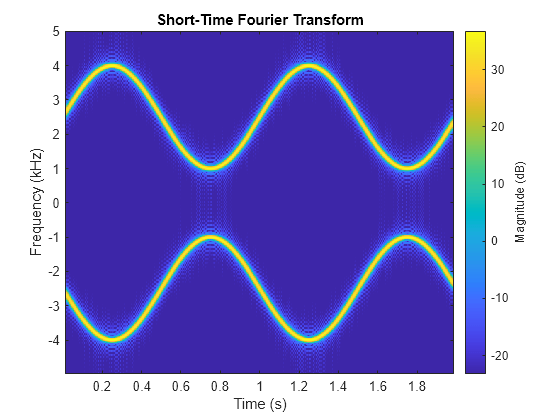
Obtain the same plot by calling the stft function with no output arguments.

stft(x,fs,Window=kaiser(256,5),OverlapLength=220,FFTLength=512)

STFT of Quadratic Chirp

Generate a quadratic chirp sampled at 1 kHz for 2 seconds. The instantaneous frequency is 100 Hz at $\mathit{t}=0$ and crosses 200 Hz at $\mathit{t}=1$ second.

ts = 0:1/1e3:2;

f0 = 100;
f1 = 200;

x = chirp(ts,f0,1,f1,"quadratic",[],"concave");

Compute and display the STFT of the quadratic chirp with a duration of 1 ms.

d = seconds(1e-3);
win = hamming(100,"periodic");

stft(x,d,Window=win,OverlapLength=98,FFTLength=128);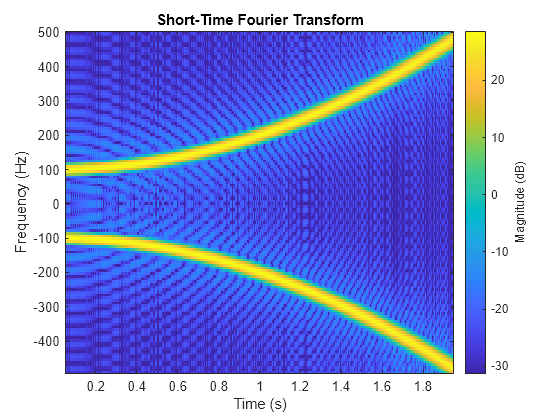

Compare spectrogram and stft Functions

Generate a signal consisting of a chirp sampled at 1.4 kHz for 2 seconds. The frequency of the chirp decreases linearly from 600 Hz to 100 Hz during the measurement time.

fs = 1400;
x = chirp(0:1/fs:2,600,2,100);

stft Defaults

Compute the STFT of the signal using the spectrogram and stft functions. Use the default values of the stft function:

• Divide the signal into 128-sample segments and window each segment with a periodic Hann window.

• Specify 96 samples of overlap between adjoining segments. This length is equivalent to 75% of the window length.

• Specify 128 DFT points and center the STFT at zero frequency, with the frequency expressed in hertz.

Verify that the two results are equal.

M = 128;
g = hann(M,"periodic");
L = 0.75*M;
Ndft = 128;

[sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered");

[s,f,t] = stft(x,fs);

dff = max(max(abs(sp-s)))

dff = 
0

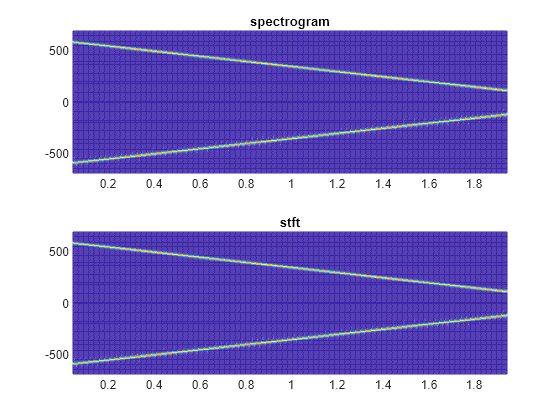
Use the mesh function to plot the two outputs.

nexttile
mesh(tp,fp,abs(sp).^2)
title("spectrogram")
view(2), axis tight

nexttile
mesh(t,f,abs(s).^2)
title("stft")
view(2), axis tight

spectrogram Defaults

Repeat the computation using the default values of the spectrogram function:

• Divide the signal into segments of length $\mathit{M}=\lfloor {\mathit{N}}_{\mathit{x}}/4.5\rfloor$, where ${\mathit{N}}_{\mathit{x}}$ is the length of the signal. Window each segment with a Hamming window.

• Specify 50% overlap between segments.

• To compute the FFT, use $\max \left(256,2^{\lceil {\log }_2\mathit{M}\rceil }\right)$ points. Compute the spectrogram only for positive normalized frequencies.

M = floor(length(x)/4.5);
g = hamming(M);
L = floor(M/2);
Ndft = max(256,2^nextpow2(M));

[sx,fx,tx] = spectrogram(x);

[st,ft,tt] = stft(x,Window=g,OverlapLength=L, ...
    FFTLength=Ndft,FrequencyRange="onesided");

dff = max(max(sx-st))

dff = 
0

Use the waterplot function to plot the two outputs. Divide the frequency axis by $\pi$ in both cases. For the stft output, divide the sample numbers by the effective sample rate, $2\pi$.

figure
nexttile
waterplot(sx,fx/pi,tx)
title("spectrogram")

nexttile
waterplot(st,ft/pi,tt/(2*pi))
title("stft")

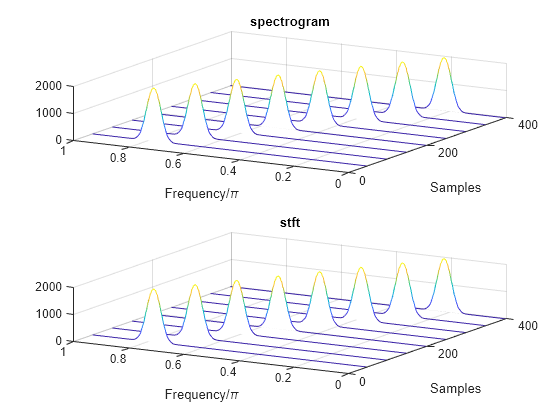
function waterplot(s,f,t)
% Waterfall plot of spectrogram
    waterfall(f,t,abs(s)'.^2)
    set(gca,XDir="reverse",View=[30 50])
    xlabel("Frequency/\pi")
    ylabel("Samples")
end

STFT Frequency Ranges

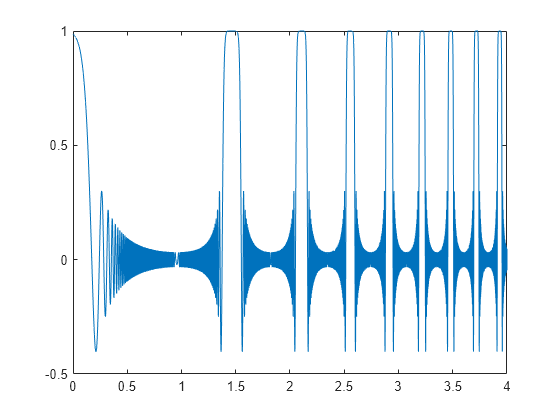
Generate a signal sampled at 5 kHz for 4 seconds. The signal consists of a set of pulses of decreasing duration separated by regions of oscillating amplitude and fluctuating frequency with an increasing trend. Plot the signal.

fs = 5000;
t = 0:1/fs:4-1/fs;

x = besselj(0,600*(sin(2*pi*(t+1).^3/30).^5));

plot(t,x)

Compute the one-sided, two-sided, and centered short-time Fourier transforms of the signal. In all cases, use a 202-sample Kaiser window with shape factor $\beta =10$ to window the signal segments. Display the frequency range used to compute each transform.

rngs = ["onesided" "twosided" "centered"];

for kj = 1:length(rngs)
    
    opts = {'Window',kaiser(202,10),'FrequencyRange',rngs(kj)};

    [~,f] = stft(x,fs,opts{:});
    subplot(length(rngs),1,kj)
    stft(x,fs,opts{:})
    title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000))

end

Repeat the computation, but now change the length of the Kaiser window to 203, an odd number. The 'twosided' frequency interval does not change. The other two frequency intervals become open at the higher end.

for kj = 1:length(rngs)
    
    opts = {'Window',kaiser(203,10),'FrequencyRange',rngs(kj)};

    [~,f] = stft(x,fs,opts{:});
    subplot(length(rngs),1,kj)
    stft(x,fs,opts{:})
    title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000))

end

STFT of Multichannel Signals

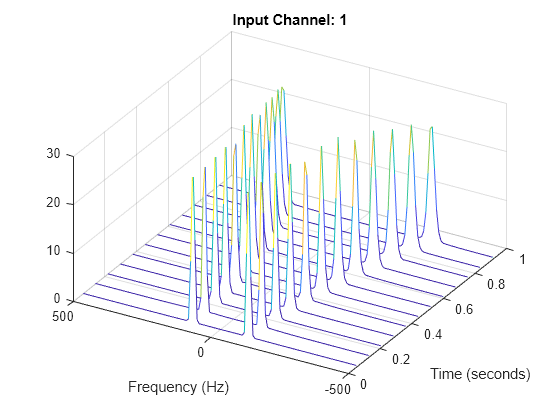
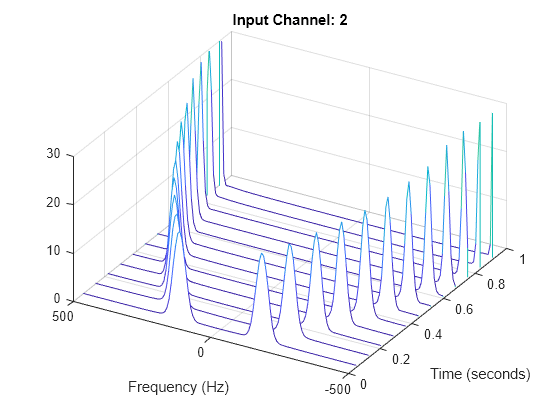
Generate a three-channel signal consisting of three different chirps sampled at 1 kHz for one second.

1. The first channel consists of a concave quadratic chirp with instantaneous frequency 100 Hz at t = 0 and crosses 300 Hz at t = 1 second. It has an initial phase equal to 45 degrees.

2. The second channel consists of a convex quadratic chirp with instantaneous frequency 100 Hz at t = 0 and crosses 500 Hz at t = 1 second.

3. The third channel consists of a logarithmic chirp with instantaneous frequency 300 Hz at t = 0 and crosses 500 Hz at t = 1 second.

Compute the STFT of the multichannel signal using a periodic Hamming window of length 128 and an overlap length of 50 samples.

fs = 1e3;
t = 0:1/fs:1-1/fs;

x = [chirp(t,100,1,300,'quadratic',45,'concave');
      chirp(t,100,1,500,'quadratic',[],'convex');
      chirp(t,300,1,500,'logarithmic')]'; 
  
[S,F,T] = stft(x,fs,'Window',hamming(128,'periodic'),'OverlapLength',50);

Visualize the STFT of each channel as a waterfall plot. Control the behavior of the axes using the helper function helperGraphicsOpt.

waterfall(F,T,abs(S(:,:,1))')
helperGraphicsOpt(1)

waterfall(F,T,abs(S(:,:,2))')
helperGraphicsOpt(2)

waterfall(F,T,abs(S(:,:,3))')
helperGraphicsOpt(3)

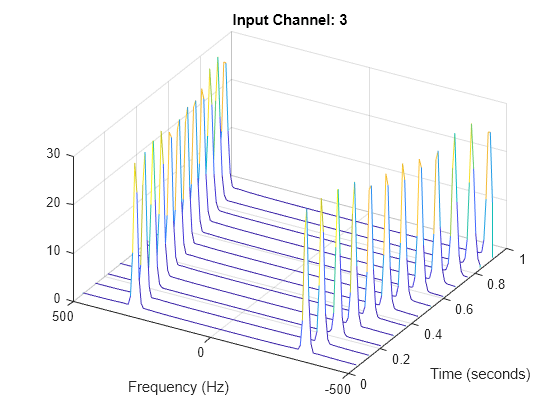
This helper function sets the appearance and behavior of the current axes.

function helperGraphicsOpt(ChannelId)
ax = gca;
ax.XDir = 'reverse';
ax.ZLim = [0 30];
ax.Title.String = ['Input Channel: ' num2str(ChannelId)];
ax.XLabel.String = 'Frequency (Hz)';
ax.YLabel.String = 'Time (seconds)';
ax.View = [30 45];
end

Input Arguments

x — Input signal

vector | matrix | timetable

Input signal, specified as a vector, a matrix, or a MATLAB^® timetable.

Note

If you want x and s to be the same length, the value of (length(x)-noverlap)/(length(window)-noverlap) must be an integer. Use Window to specify the length of window and OverlapLength to specify noverlap.

• If the input has multiple channels, specify x as a matrix where each column corresponds to a channel.

• For timetable input, x must contain uniformly increasing finite row times. If a timetable has missing or duplicate time points, you can fix it using the tips in Clean Timetable with Missing, Duplicate, or Nonuniform Times.

• For multichannel timetable input, specify x as a timetable with a single variable containing a matrix or a timetable with multiple variables each containing a column vector. All variables must have the same precision.

Each channel of x must have a length greater than or equal to the window length.

Example: chirp(0:1/4e3:2,250,1,500,"quadratic") specifies a single-channel chirp.

Example: timetable(rand(5,2),SampleRate=1) specifies a two-channel random variable sampled at 1 Hz for 4 seconds.

Example: timetable(rand(5,1),rand(5,1),SampleRate=1) specifies a two-channel random variable sampled at 1 Hz for 4 seconds.

Data Types: double | single
Complex Number Support: Yes

fs — Sample rate

2π (default) | positive scalar

Sample rate, specified as a positive scalar. This argument applies only when x is a vector or a matrix.

Data Types: double | single

ts — Sample time

duration scalar

Sample time, specified as a duration scalar. This argument applies only when x is a vector or a matrix

Example: seconds(1) is a duration scalar representing a 1-second time difference between consecutive signal samples.

Data Types: duration

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: Window=hamming(100),OverlapLength=50,FFTLength=128 windows the data using a 100-sample Hamming window, with 50 samples of overlap between adjoining segments and a 128-point FFT.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Window',hamming(100),'OverlapLength',50,'FFTLength',128 windows the data using a 100-sample Hamming window, with 50 samples of overlap between adjoining segments and a 128-point FFT.

Window — Spectral window

hann(128,"periodic") (default) | vector

Spectral window, specified as a vector. If you do not specify the window or specify it as empty, the function uses a Hann window of length 128. The length of Window must be greater than or equal to 2.

For a list of available windows, see Windows.

Example: hann(N+1) and (1-cos(2*pi*(0:N)'/N))/2 both specify a Hann window of length N + 1.

Data Types: double | single

OverlapLength — Number of overlapped samples

75% of window length (default) | nonnegative integer

Number of overlapped samples, specified as a positive integer smaller than the length of Window. If you omit OverlapLength or specify it as empty, it is set to the largest integer less than 75% of the window length, which is 96 samples for the default Hann window.

Data Types: double | single

FFTLength — Number of DFT points

128 (default) | positive integer

Number of DFT points, specified as a positive integer. The value must be greater than or equal to the window length. If the length of the input signal is less than the DFT length, the data is padded with zeros.

Data Types: double | single

FrequencyRange — STFT frequency range

"centered" (default) | "twosided" | "onesided"

STFT frequency range, specified as "centered", "twosided", or "onesided".

• "centered" — Compute a two-sided, centered STFT. If FFTLength is even, then s is computed over the interval (–π, π] rad/sample. If FFTLength is odd, then s is computed over the interval (–π, π) rad/sample. If you specify time information, then the intervals are (–f_s, f_s/2] cycles/unit time and (–f_s, f_s/2) cycles/unit time, respectively, where f_s is the effective sample rate.

• "twosided" — Compute a two-sided STFT over the interval [0, 2π) rad/sample. If you specify time information, then the interval is [0, f_s) cycles/unit time.

• "onesided" — Compute a one-sided STFT. If FFTLength is even, then s is computed over the interval [0, π] rad/sample. If FFTLength is odd, then s is computed over the interval [0, π) rad/sample. If you specify time information, then the intervals are [0, f_s/2] cycles/unit time and [0, f_s/2) cycles/unit time, respectively, where f_s is the effective sample rate. This option is valid only for real signals.

  Note

  When this argument is set to "onesided", stft outputs the values in the positive Nyquist range and does not conserve the total power.

For an example, see STFT Frequency Ranges.

Data Types: char | string

OutputTimeDimension — Output time dimension

"acrosscolumns" (default) | "downrows"

Output time dimension, specified as "acrosscolumns" or "downrows". Set this value to "downrows" if you want the time dimension of s down the rows and the frequency dimension across the columns. Set this value to "acrosscolumns" if you want the time dimension of s across the columns and the frequency dimension down the rows. This input is ignored if the function is called without output arguments.

Output Arguments

s — Short-time Fourier transform

matrix | 3-D array

Short-time Fourier transform, returned as a matrix or a 3-D array. Time increases across the columns of s and frequency increases down the rows. The third dimension, if present, corresponds to the input channels.

• If the signal x has N_x time samples, then s has k columns, where k = ⌊(N_x–L)/(M–L)⌋, M is the length of Window, L is the OverlapLength, and the ⌊ ⌋ symbols denote the floor function.

• The number of rows in s is equal to the value specified in FFTLength.

Data Types: double | single

f — Frequencies

vector

Frequencies at which the STFT is evaluated, returned as a vector.

Data Types: double | single

t — Time instants

vector

Time instants, returned as a vector. t contains the time values corresponding to the centers of the data segments used to compute short-time power spectrum estimates.

• If a sample rate fs is provided, then the vector contains time values in seconds.

• If a sample time ts is provided, then the vector is a duration array with the same time format as the input.

• If no time information is provided, then the vector contains sample numbers.

Data Types: double | single

More About

Short-Time Fourier Transform

The short-time Fourier transform (STFT) is used to analyze how the frequency content of a nonstationary signal changes over time. The magnitude squared of the STFT is known as the spectrogram time-frequency representation of the signal. For more information about the spectrogram and how to compute it using Signal Processing Toolbox™ functions, see Spectrogram Computation with Signal Processing Toolbox.

The STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. Most window functions taper off at the edges to avoid spectral ringing. The DFT of each windowed segment is added to a complex-valued matrix that contains the magnitude and phase for each point in time and frequency. The STFT matrix has

$$k=\lfloor \frac{N_x-L}{M-L}\rfloor$$

columns, where N_x is the length of the signal x(n) and the ⌊⌋ symbols denote the floor function. The number of rows in the matrix equals N_DFT, the number of DFT points, for centered and two-sided transforms and an odd number close to N_DFT/2 for one-sided transforms of real-valued signals.

The mth column of the STFT matrix $$X(f)=\left[\begin{array}{ccccc}{X}_1(f)& X_2(f)& X_3(f)& \cdots & X_k(f)\end{array}\right]$$ contains the DFT of the windowed data centered about time mR:

$$X_m(f)={\displaystyle \sum _{n=-\infty }^{\infty }x(n)g(n-mR)e^{-j2\pi fn}}.$$

References

[1] Mitra, Sanjit K. Digital Signal Processing: A Computer-Based Approach. 2nd Ed. New York: McGraw-Hill, 2001.

[2] Sharpe, Bruce. Invertibility of Overlap-Add Processing. https://gauss256.github.io/blog/cola.html, accessed July 2019.

[3] Smith, Julius Orion. Spectral Audio Signal Processing. https://ccrma.stanford.edu/~jos/sasp/, online book, 2011 edition, accessed Nov 2018.

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

The stft function supports tall arrays with the following usage notes and limitations:

OutputTimeDimension must always be specified and set to "downrows".

For more information, see Tall Arrays.

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation

Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

Timetables are not supported for code generation.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

Usage notes and limitations:

• The syntax with no output arguments is not supported.

For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced in R2019a