Spectrogram Computation with Signal Processing Toolbox
Signal Processing Toolbox™ provides three functions that compute the spectrogram of a nonstationary signal. Each of the functions has different input arguments, default values, and outputs. The best choice for you depends on your particular application.
A nonstationary signal is a signal whose frequency content changes over time. The short-time Fourier transform (STFT) is used to analyze how this frequency content changes as the signal evolves. The magnitude squared of the STFT is known as the spectrogram time-frequency representation of the signal.
The spectrogram is only one of several possible time-frequency representations. For an
overview of other time-frequency representations available in Signal Processing Toolbox and Wavelet Toolbox™, see Time-Frequency Gallery. For a treatment of
stationary signals using the periodogram function, see Power Spectral Density Estimates Using FFT.
Functions for Spectrogram Computation
Signal Processing Toolbox has these functions that can be used to compute the spectrogram:
spectrogram— Designed for maximum flexibility. Computes STFT and segment-by-segment power spectral densities or power spectra. Supports reassignment.stft— Designed for invertibility and maximum control. Computes STFT. Used bydlstftandstftLayer. Supports multichannel input. Its counterpart, theistftfunction, computes the inverse STFT.pspectrum— Designed for ease of use. Computes power spectra. Used in the analysis scripts generated by Signal Analyzer. Can compute spectra of stationary signals and persistence spectra. Supports reassignment.
The spectrogram function is used as reference in the
discussion that follows.
| Category | Parameters | Function | ||
|---|---|---|---|---|
spectrogram | stft | pspectrum | ||
| Input | Signal | Vector with Nx elements |
|
|
| Window, g(n) | Second positional argument (Default: Hamming window) |
(Default: Periodic Hann window) | Kaiser window only | |
| Window length, M | Specified as number of samples (Default: ⌊Nx/4.5⌋) | Specified as number of samples (Default: 128) | TimeResolution name-value argument | |
| Leakage, ℓ |
|
| Leakage name-value argument related to Kaiser window
β shape factor: ℓ = 1 – β/40 | |
| Overlap, L | Number of samples specified as third positional argument (Default: 50% of window length) | Number of samples specified with (Default: 75% of window length) | Percentage of segment length specified with (Default: where ENBW is the equivalent noise bandwidth of the window) | |
| Number of DFT points, NDFT | Fourth positional argument (Default: max(256,2⌈log2M⌉)) |
(Default: 128) | Always 1024 | |
| Time information | Sample rate specified as fifth positional argument | Sample rate or time vector specified as second positional argument | Sample rate or time vector specified as second positional argument | |
| Function call |
fs = 100;
x = exp(2j*pi*20* ...
(0:1/fs:2-1/fs));
M = 200; lk = 0.5;
g = kaiser(M,40*(1-lk));
L = 100; Ndft = 1024; |
sps = abs( ...
spectrogram(x,g,L, ...
Ndft,fs,"centered") ...
).^2; |
sts = abs( ...
stft(x,fs,Window=g, ...
OverlapLength=L, ...
FFTLength=Ndft) ...
).^2; |
pss = pspectrum(x,fs, ...
"spectrogram", ...
TimeResolution=M/fs, ...
Leakage=lk, ...
OverlapPercent=L/M*100 ...
)*sum(g)^2; |
| Convenience plot |
fs = 6e2;
ts = 0:1/fs:2.05;
x = vco(sin(2*pi*ts).* ...
exp(-ts),[0.1 0.4]*fs,fs);
M = 32; lk = 0.9;
g = kaiser(M,40*(1-lk));
L = 22; Ndft = 1024;
|
|
|
|
| Output | Frequency range |
| Controlled using
| Controlled using
|
| Time interval |
|
|
| |
| Normalization |
| First output argument is STFT. Its magnitude squared is the spectrogram. |
| |
| PSD and power spectrum |
| Output argument is STFT. |
| |
| Examples | ||||
STFT and Spectrogram Definitions
The STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. Most window functions taper off at the edges to avoid spectral ringing. The DFT of each windowed segment is added to a complex-valued matrix that contains the magnitude and phase for each point in time and frequency. The STFT matrix has
columns, where Nx is the length of the signal x(n) and the ⌊⌋ symbols denote the floor function. The number of rows in the matrix equals NDFT, the number of DFT points, for centered and two-sided transforms and an odd number close to NDFT/2 for one-sided transforms of real-valued signals.
The mth column of the STFT matrix contains the DFT of the windowed data centered about time mR:
Compare spectrogram Function and STFT Definition
Generate a signal that consists of a complex-valued convex quadratic chirp sampled at 600 Hz for 2 seconds. The chirp has an initial frequency of 250 Hz and a final frequency of 50 Hz.
fs = 6e2; ts = 0:1/fs:2; x = chirp(ts,250,ts(end),50,"quadratic",0,"convex","complex");
spectrogram Function
Use the spectrogram function to compute the STFT of the signal.
Divide the signal into segments, each samples long.
Specify samples of overlap between adjoining segments.
Discard the final, shorter segment.
Window each segment with a Bartlett window.
Evaluate the discrete Fourier transform of each segment at points. By default,
spectrogramcomputes two-sided transforms for complex-valued signals.
M = 49; L = 11; g = bartlett(M); Ndft = 1024; [s,f,t] = spectrogram(x,g,L,Ndft,fs);
Use the waterplot function to compute and display the spectrogram, defined as the magnitude squared of the STFT.
waterplot(s,f,t)

STFT Definition
Compute the STFT of the -sample signal using the definition. Divide the signal into overlapping segments. Window each segment and evaluate its discrete Fourier transform at points.
segs = framesig(1:length(x),M,OverlapLength=L); X = fft(x(segs).*g,Ndft);
Compute the time and frequency ranges for the STFT.
To find the time values, divide the time vector into overlapping segments. The time values are the midpoints of the segments, with each segment treated as an interval open at the lower end.
To find the frequency values, specify a Nyquist interval closed at zero frequency and open at the lower end.
framedT = ts(segs); tint = mean(framedT(2:end,:)); fint = 0:fs/Ndft:fs-fs/Ndft;
Compare the output of spectrogram to the definition. Display the spectrogram.
maxdiff = max(max(abs(s-X)))
maxdiff = 0
waterplot(X,fint,tint)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
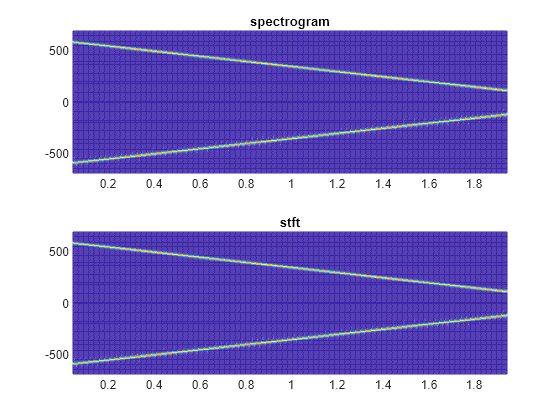
Compare spectrogram and stft Functions
Generate a signal consisting of a chirp sampled at 1.4 kHz for 2 seconds. The frequency of the chirp decreases linearly from 600 Hz to 100 Hz during the measurement time.
fs = 1400; x = chirp(0:1/fs:2,600,2,100);
stft Defaults
Compute the STFT of the signal using the spectrogram and stft functions. Use the default values of the stft function:
Divide the signal into 128-sample segments and window each segment with a periodic Hann window.
Specify 96 samples of overlap between adjoining segments. This length is equivalent to 75% of the window length.
Specify 128 DFT points and center the STFT at zero frequency, with the frequency expressed in hertz.
Verify that the two results are equal.
M = 128; g = hann(M,"periodic"); L = 0.75*M; Ndft = 128; [sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered"); [s,f,t] = stft(x,fs); dff = max(max(abs(sp-s)))
dff = 0
Use the mesh function to plot the two outputs.
nexttile mesh(tp,fp,abs(sp).^2) title("spectrogram") view(2), axis tight nexttile mesh(t,f,abs(s).^2) title("stft") view(2), axis tight
spectrogram Defaults
Repeat the computation using the default values of the spectrogram function:
Divide the signal into segments of length , where is the length of the signal. Window each segment with a Hamming window.
Specify 50% overlap between segments.
To compute the FFT, use points. Compute the spectrogram only for positive normalized frequencies.
M = floor(length(x)/4.5); g = hamming(M); L = floor(M/2); Ndft = max(256,2^nextpow2(M)); [sx,fx,tx] = spectrogram(x); [st,ft,tt] = stft(x,Window=g,OverlapLength=L, ... FFTLength=Ndft,FrequencyRange="onesided"); dff = max(max(sx-st))
dff = 0
Use the waterplot function to plot the two outputs. Divide the frequency axis by in both cases. For the stft output, divide the sample numbers by the effective sample rate, .
figure nexttile waterplot(sx,fx/pi,tx) title("spectrogram") nexttile waterplot(st,ft/pi,tt/(2*pi)) title("stft")
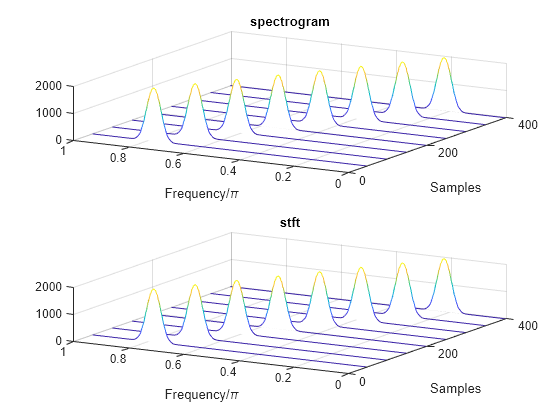
function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency/\pi") ylabel("Samples") end
Compare spectrogram and pspectrum Functions
Generate a signal that consists of a voltage-controlled oscillator and three Gaussian atoms. The signal is sampled at kHz for 2 seconds.
fs = 2000; tx = 0:1/fs:2; gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.03^2)).*sin(2*pi*f.*x)*A'; s = gaussFun([1 1 1],tx',[0.1 0.65 1],[2 6 2]*100)*1.5; x = vco(chirp(tx+.1,0,tx(end),3).*exp(-2*(tx-1).^2),[0.1 0.4]*fs,fs); x = s+x';
Short-Time Fourier Transforms
Use the pspectrum function to compute the STFT.
Divide the -sample signal into segments of length samples, corresponding to a time resolution of milliseconds.
Specify samples or 20% of overlap between adjoining segments.
Window each segment with a Kaiser window and specify a leakage .
M = 80; L = 16; lk = 0.7; [S,F,T] = pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk);
Compare to the result obtained with the spectrogram function.
Specify the window length and overlap directly in samples.
pspectrumalways uses a Kaiser window as . The leakage and the shape factor of the window are related by .pspectrumalways uses points when computing the discrete Fourier transform. You can specify this number if you want to compute the transform over a two-sided or centered frequency range. However, for one-sided transforms, which are the default for real signals,spectrogramuses points. Alternatively, you can specify the vector of frequencies at which you want to compute the transform, as in this example.If a signal cannot be divided exactly into segments,
spectrogramtruncates the signal whereaspspectrumpads the signal with zeros to create an extra segment. To make the outputs equivalent, remove the final segment and the final element of the time vector.spectrogramreturns the STFT, whose magnitude squared is the spectrogram.pspectrumreturns the segment-by-segment power spectrum, which is already squared but is divided by a factor of before squaring.For one-sided transforms,
pspectrumadds an extra factor of 2 to the spectrogram.
g = kaiser(M,40*(1-lk)); k = (length(x)-L)/(M-L); if k~=floor(k) S = S(:,1:floor(k)); T = T(1:floor(k)); end [s,f,t] = spectrogram(x/sum(g)*sqrt(2),g,L,F,fs);
Use the waterplot function to display the spectrograms computed by the two functions.
subplot(2,1,1) waterplot(sqrt(S),F,T) title("pspectrum") subplot(2,1,2) waterplot(s,f,t) title("spectrogram")

maxd = max(max(abs(abs(s).^2-S)))
maxd = 2.4419e-08
Power Spectra and Convenience Plots
The spectrogram function has a fourth argument that corresponds to the segment-by-segment power spectrum or power spectral density. Similar to the output of pspectrum, the ps argument is already squared and includes the normalization factor . For one-sided spectrograms of real signals, you still have to include the extra factor of 2. Set the scaling argument of the function to "power".
[~,~,~,ps] = spectrogram(x*sqrt(2),g,L,F,fs,"power");
max(abs(S(:)-ps(:)))ans = 2.4419e-08
When called with no output arguments, both pspectrum and spectrogram plot the spectrogram of the signal in decibels. Include the factor of 2 for one-sided spectrograms. Set the colormaps to be the same for both plots. Set the x-limits to the same values to make visible the extra segment at the end of the pspectrum plot. In the spectrogram plot, display the frequency on the y-axis.
subplot(2,1,1) pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk) title("pspectrum") cc = clim; xl = xlim; subplot(2,1,2) spectrogram(x*sqrt(2),g,L,F,fs,"power","yaxis") title("spectrogram") clim(cc) xlim(xl)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
Compute Centered and One-Sided Spectrograms
Generate a signal that consists of a real-valued chirp sampled at 2 kHz for 2 seconds.
fs = 2000;
tx = 0:1/fs:2;
x = vco(-chirp(tx,0,tx(end),2).*exp(-3*(tx-1).^2), ...
[0.1 0.4]*fs,fs).*hann(length(tx))';Two-Sided Spectrogram
Compute and plot the two-sided STFT of the signal.
Divide the signal into segments, each samples long.
Specify samples of overlap between adjoining segments.
Discard the final, shorter segment.
Window each segment with a flat-top window.
Evaluate the discrete Fourier transform of each segment at points, noting that it is an odd number.
M = 73;
L = 24;
g = flattopwin(M);
Ndft = 895;
neven = ~mod(Ndft,2);
[stwo,f,t] = spectrogram(x,g,L,Ndft,fs,"twosided");Use the spectrogram function with no output arguments to plot the two-sided spectrogram.
spectrogram(x,g,L,Ndft,fs,"twosided","power","yaxis")

Compute the two-sided spectrogram using the definition. Divide the signal into -sample segments with samples of overlap between adjoining segments. Window each segment and compute its discrete Fourier transform at points.
y = framesig(x,M,Window=g,OverlapLength=L); Xtwo = fft(y,Ndft);
Compute the time and frequency ranges.
To find the time values, divide the time vector into overlapping segments. The time values are the midpoints of the segments, with each segment treated as an interval open at the lower end.
To find the frequency values, specify a Nyquist interval closed at zero frequency and open at the upper end.
framedT = framesig(tx,M,OverlapLength=L); ttwo = mean(framedT(2:end,:)); ftwo = 0:fs/Ndft:fs*(1-1/Ndft);
Compare the outputs of spectrogram to the definitions. Use the waterplot function to display the spectrograms.
diffs = [max(max(abs(stwo-Xtwo)));
max(abs(f-ftwo'));
max(abs(t-ttwo))]diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xtwo,ftwo,ttwo) title("Two-Sided, Definition") nexttile waterplot(stwo,f,t) title("Two-Sided, spectrogram Function")

Centered Spectrogram
Compute the centered spectrogram of the signal.
Use the same time values that you used for the two-sided STFT.
Use the
fftshiftfunction to shift the zero-frequency component of the STFT to the center of the spectrum.For odd-valued , the frequency interval is open at both ends. For even-valued , the frequency interval is open at the lower end and closed at the upper end.
Compare the outputs and display the spectrograms.
tcen = ttwo; if ~neven Xcen = fftshift(Xtwo,1); fcen = -fs/2*(1-1/Ndft):fs/Ndft:fs/2; else Xcen = fftshift(circshift(Xtwo,-1),1); fcen = (-fs/2*(1-1/Ndft):fs/Ndft:fs/2)+fs/Ndft/2; end [scen,f,t] = spectrogram(x,g,L,Ndft,fs,"centered"); diffs = [max(max(abs(scen-Xcen))); max(abs(f-fcen')); max(abs(t-tcen))]
diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xcen,fcen,tcen) title("Centered, Definition") nexttile waterplot(scen,f,t) title("Centered, spectrogram Function")

One-Sided Spectrogram
Compute the one-sided spectrogram of the signal.
Use the same time values that you used for the two-sided STFT.
For odd-valued , the one-sided STFT consists of the first rows of the two-sided STFT. For even-valued , the one-sided STFT consists of the first rows of the two-sided STFT.
For odd-valued , the frequency interval is closed at zero frequency and open at the Nyquist frequency. For even-valued , the frequency interval is closed at both ends.
Compare the outputs and display the spectrograms. For real-valued signals, the "onesided" argument is optional.
tone = ttwo; if ~neven Xone = Xtwo(1:(Ndft+1)/2,:); else Xone = Xtwo(1:Ndft/2+1,:); end fone = 0:fs/Ndft:fs/2; [sone,f,t] = spectrogram(x,g,L,Ndft,fs); diffs = [max(max(abs(sone-Xone))); max(abs(f-fone')); max(abs(t-tone))]
diffs = 3×1
10-12 ×
0
0.1137
0.0002
figure nexttile waterplot(Xone,fone,tone) title("One-Sided, Definition") nexttile waterplot(sone,f,t) title("One-Sided, spectrogram Function")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
Compute Segment PSDs and Power Spectra
The spectrogram function has a matrix containing either the power spectral density (PSD) or the power spectrum of each segment as the fourth output argument. The power spectrum is equal to the PSD multiplied by the equivalent noise bandwidth (ENBW) of the window.
Generate a signal that consists of a logarithmic chirp sampled at 1 kHz for 1 second. The chirp has an initial frequency of 400 Hz that decreases to 10 Hz by the end of the measurement.
fs = 1000;
tt = 0:1/fs:1-1/fs;
y = chirp(tt,400,tt(end),10,"logarithmic");Segment PSDs and Power Spectra with Sample Rate
Divide the signal into 102-sample segments and window each segment with a Hann window. Specify 12 samples of overlap between adjoining segments and 1024 DFT points.
M = 102; g = hann(M); L = 12; Ndft = 1024;
Compute the spectrogram of the signal with the default PSD spectrum type. Output the STFT and the array of segment power spectral densities.
[s,f,t,p] = spectrogram(y,g,L,Ndft,fs);
Repeat the computation with the spectrum type specified as "power". Output the STFT and the array of segment power spectra.
[r,~,~,q] = spectrogram(y,g,L,Ndft,fs,"power");Verify that the spectrogram is the same in both cases. Plot the spectrogram using a logarithmic scale for the frequency.
max(max(abs(s).^2-abs(r).^2))
ans = 0
waterfall(f,t,abs(s)'.^2) set(gca,XScale="log",... XDir="reverse",View=[30 50])

Verify that the power spectra are equal to the power spectral densities multiplied by the ENBW of the window.
max(max(abs(q-p*enbw(g,fs))))
ans = 1.1102e-16
Verify that the matrix of segment power spectra is proportional to the spectrogram. The proportionality factor is the square of the sum of the window elements.
max(max(abs(s).^2-q*sum(g)^2))
ans = 0
Segment PSDs and Power Spectra with Normalized Frequencies
Repeat the computation, but now work in normalized frequencies. The results are the same when you specify the sample rate as .
[~,~,~,pn] = spectrogram(y,g,L,Ndft);
[~,~,~,qn] = spectrogram(y,g,L,Ndft,"power");
max(max(abs(qn-pn*enbw(g,2*pi))))ans = 1.1102e-16
See Also
Apps
Functions
dlstft|dlistft|pspectrum|spectrogram|stft|istft|xspectrogram


