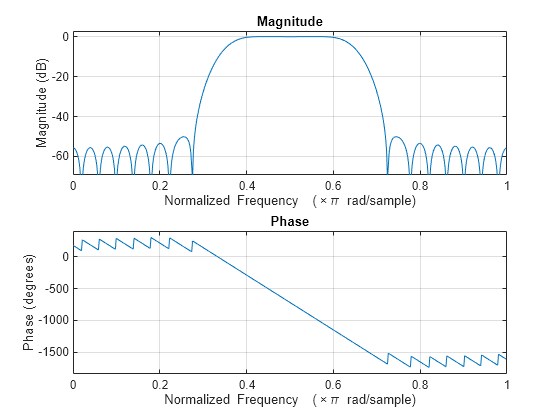
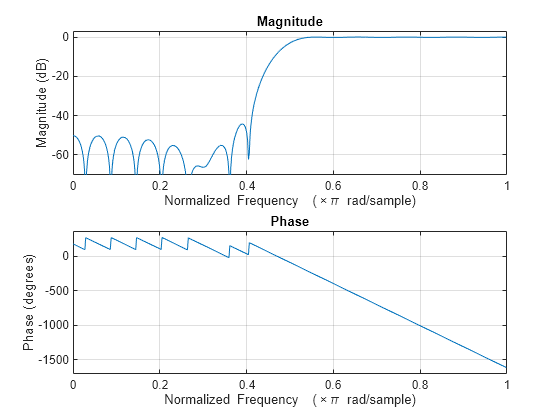
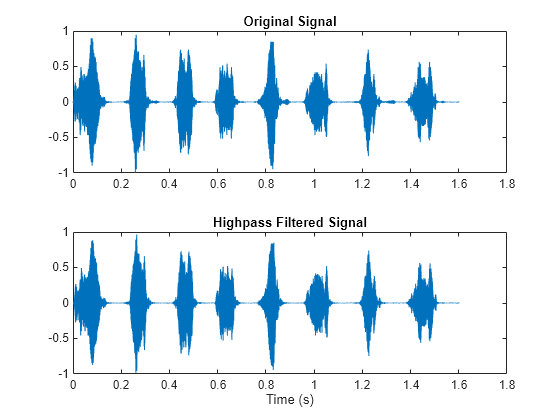
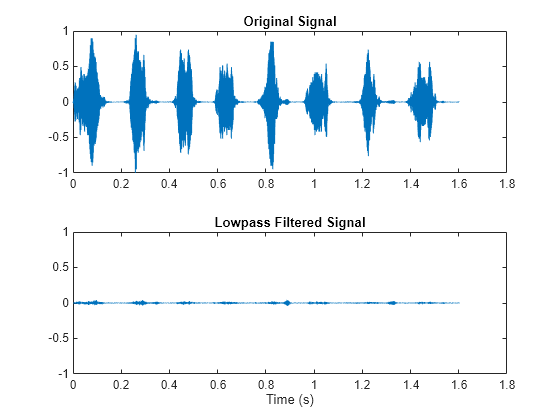
fir1
Window-based FIR filter design
Description
Examples
Input Arguments
Output Arguments
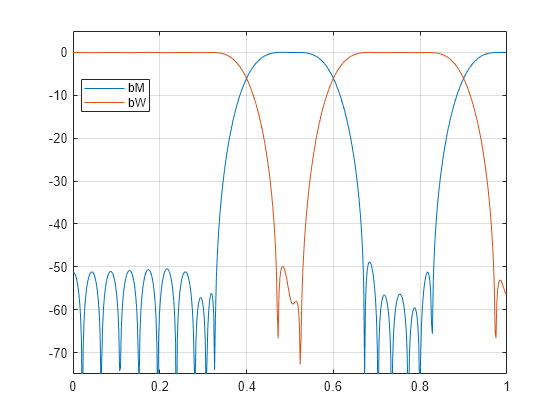
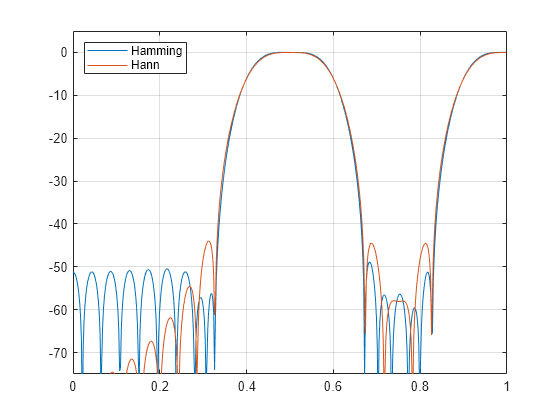
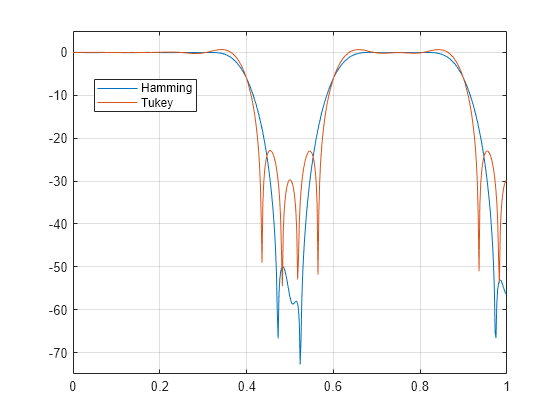
Algorithms
fir1 uses a least-squares approximation to
compute the filter coefficients and then smooths the impulse response
with window.
References
[1] Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979, Algorithm 5.2.