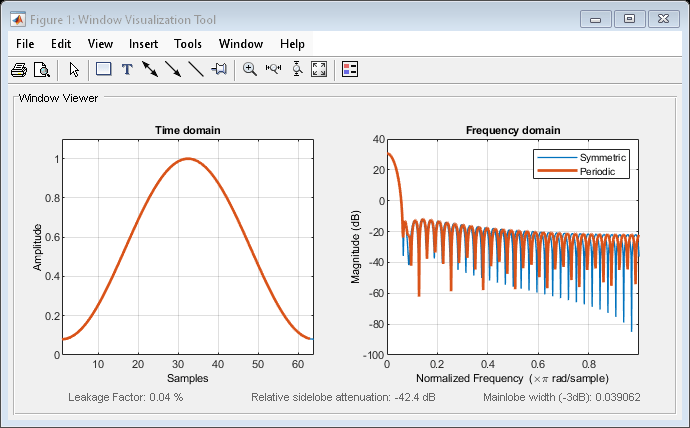
hamming
Hamming window
Description
Examples
Input Arguments
Output Arguments
Algorithms
The following equation generates the coefficients of a Hamming window:
The window length L = N + 1.
References
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999.