filtfilt
Zero-phase digital filtering
Syntax
Description
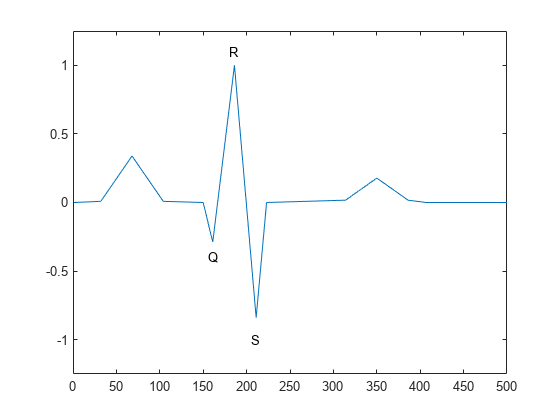
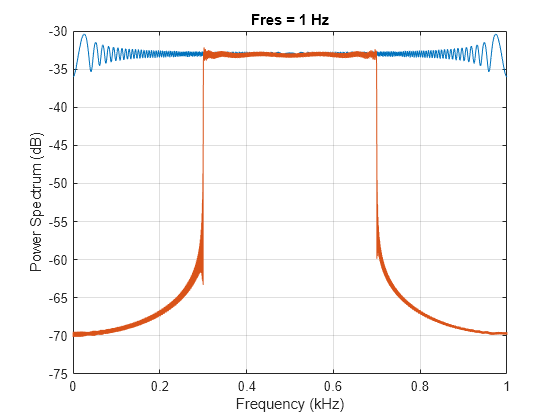
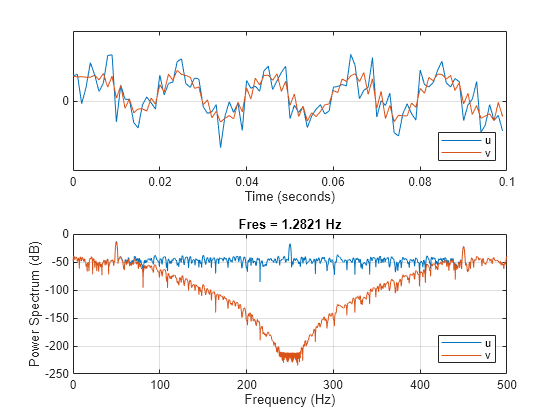
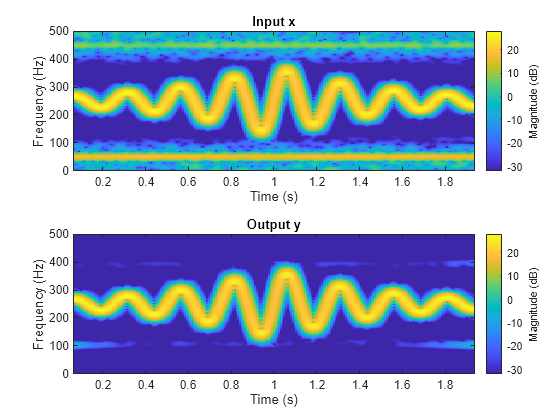
y = filtfilt(b,a,x)x in both the forward and reverse directions. After
filtering the data in the forward direction, the function matches initial
conditions to minimize startup and ending transients, reverses the filtered
sequence, and runs the reversed sequence back through the filter. The result has
these characteristics:
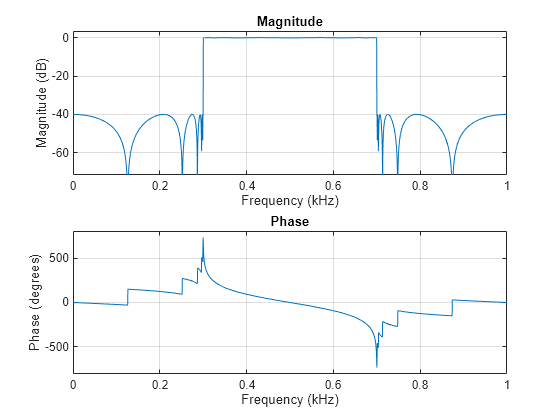
Zero phase distortion
A filter transfer function equal to the squared magnitude of the original filter transfer function
A filter order that is double the order of the filter specified by
banda
filtfilt implements the algorithm
proposed by Gustafsson [1].
Do not use filtfilt with differentiator and Hilbert
FIR filters, because the operation of those filters depends heavily on their
phase response.
y = filtfilt(d,x)x using a digital filter
d. Use designfilt to generate
d based on frequency-response specifications.
y = filtfilt(B,A,x,"ctf")x using Cascaded Transfer Functions (CTF) defined by the numerator and denominator coefficients
B and A, respectively. (since R2024b)
Note
Specify the "ctf" option to disambiguate CTF
numerator matrices B with six columns from
second-order section matrix inputs, sos, when you
specify A as a scalar or vector.
Examples
Input Arguments
Output Arguments
More About
Tips
References
[1] Gustafsson, F. “Determining the initial states in forward-backward filtering.” IEEE® Transactions on Signal Processing. Vol. 44, April 1996, pp. 988–992. https://doi.org/10.1109/78.492552.
[2] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.
[3] Mitra, Sanjit K. Digital Signal Processing. 2nd Ed. New York: McGraw-Hill, 2001.
[4] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.