UIAxes Properties
UI axes appearance and behavior
UIAxes properties control the appearance and
behavior of a UIAxes object. By changing property
values, you can modify certain aspects of the axes.
ax = uiaxes;
ax.Color = 'blue';The properties listed here are valid for axes in App Designer, or in figures created
with the uifigure function. For axes used in GUIDE, or in apps
created with the figure function, see Axes Properties.
Font
Font name, specified as a system supported font name. The default font depends on the specific operating system and locale.
If the specified font is not available, then MATLAB® uses the best match among the fonts available on the system where the app is running.
Example: 'Arial'
Font size, specified as a scalar numeric value. The font size affects the title, axis labels, and tick labels. It also affects any legends or colorbars associated with the axes. By default, the font size is measured in pixels. The default font size depends on the specific operating system and locale.
MATLAB automatically scales some of the text to a percentage of the axes font size.
Titles and axis labels — 110% of the axes font size by default. To control the scaling, use the
TitleFontSizeMultiplierandLabelFontSizeMultiplierproperties.Legends and colorbars — 90% of the axes font size by default. To specify a different font size, set the
FontSizeproperty for theLegendorColorbarobject instead.
Example: ax.FontSize = 12
Selection mode for the font size, specified as one of these values:
'auto'— Font size specified by MATLAB. If you resize the axes to be smaller than the default size, the font size might scale down to improve readability and layout.'manual'— Font size specified manually. Do not scale the font size as the axes size changes. To specify the font size, set theFontSizeproperty.
Character thickness, specified as 'normal' or
'bold'.
MATLAB uses the FontWeight property to select a font from
those available on your system. Not all fonts have a bold weight. Therefore, specifying
a bold font weight can still result in the normal font weight.
Character slant, specified as 'normal' or
'italic'.
Not all fonts have both font styles. Therefore, the italic font might look the same as the normal font.
Scale factor for the label font size, specified as a numeric value greater
than 0. The scale factor is applied to the value of the
FontSize property to determine the font size for
the x-axis, y-axis, and
z-axis labels.
Example: ax.LabelFontSizeMultiplier = 1.5
Scale factor for the title font size, specified as a numeric value greater than 0. The scale factor is applied to the value of the FontSize property to determine the font size for the title.
Title character thickness, specified as one of these values:
'normal'— Default weight as defined by the particular font'bold'— Thicker characters than normal
Subtitle character thickness, specified as one of these values:
'normal'— Default weight as defined by the particular font'bold'— Thicker characters than normal
Font size units, specified as one of the values in this table.
Units | Description |
|---|---|
'points' | Points. One point equals 1/72 inch. |
'inches' | Inches. |
'centimeters' | Centimeters. |
'normalized'
| Interpret font size as a fraction of the axes height.
If you resize the axes, the font size modifies
accordingly. For example, if the
FontSize is
0.1 in normalized units, then the
text is 1/10 of the height value stored in the axes
Position property. |
'pixels' | Pixels. On Windows® and Macintosh systems, the size of a pixel is 1/96th of an inch. This size is independent of your system resolution. On Linux® systems, the size of a pixel is determined by your system resolution. |
To set both the font size and the font units in a single function call,
you first must set the FontUnits property so that the
UIAxes object correctly interprets the specified font
size.
Ticks
Tick values, specified as a vector of increasing values. If you do not
want tick marks along the axis, then specify an empty vector
[]. The tick values are the locations along the axis
where the tick marks appear. The tick labels are the labels that you see
next to each tick mark. Use the XTickLabels,
YTickLabels, and ZTickLabels
properties to specify the associated labels.
Example: ax.XTick = [2 4 6 8 10]
Example: ax.YTick = 0:10:100
Alternatively, use the xticks, yticks, and zticks functions to specify
the tick values. For an example, see Specify Axis Tick Values and Labels.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
Selection mode for the tick values, specified as one of these values:
'auto'— Automatically select the tick values based on the range of data for the axis.'manual'— Manually specify the tick values. To specify the values, set theXTick,YTick, orZTickproperty.
Example: ax.XTickMode = 'auto'
Tick labels, specified as a cell array of character vectors, string array,
or categorical array. If you do not want tick labels to show, then specify
an empty cell array {}. If you do not specify enough
labels for all the ticks values, then the labels repeat.
Tick labels support TeX and LaTeX markup. See the
TickLabelInterpreter property for more
information.
If you specify this property as a categorical array, MATLAB uses the values in the array, not the categories.
As an alternative to setting this property, you can use the xticklabels, yticklabels, and zticklabels functions. For
an example, see Specify Axis Tick Values and Labels.
Example: ax.XTickLabel =
{'Jan','Feb','Mar','Apr'}
Selection mode for the tick labels, specified as one of these values:
'auto'— Automatically select the tick labels.'manual'— Manually specify the tick labels. To specify the labels, set theXTickLabel,YTickLabel, orZTickLabelproperty.
Example: ax.XTickLabelMode = 'auto'
Tick label interpreter, specified as one of these values:
'tex'— Interpret labels using a subset of the TeX markup.'latex'— Interpret labels using a subset of LaTeX markup. When you specify the tick labels, use dollar signs around each element in the cell array.'none'— Display literal characters.
TeX Markup
By default, MATLAB supports a subset of TeX markup. Use TeX markup to add superscripts and subscripts, modify the text type and color, and include special characters in the labels.
Modifiers remain in effect until the end of the text.
Superscripts and subscripts are an exception because they modify only the next character or the
characters within the curly braces. When you set the interpreter to "tex",
the supported modifiers are as follows.
| Modifier | Description | Example |
|---|---|---|
^{ } | Superscript | "text^{superscript}" |
_{ } | Subscript | "text_{subscript}" |
\bf | Bold font | "\bf text" |
\it | Italic font | "\it text" |
\sl | Oblique font (usually the same as italic font) | "\sl text" |
\rm | Normal font | "\rm text" |
\fontname{ | Font name — Replace
| "\fontname{Courier} text" |
\fontsize{ | Font size —Replace
| "\fontsize{15} text" |
\color{ | Font color — Replace
red, green,
yellow, magenta,
blue, black,
white, gray,
darkGreen, orange, or
lightBlue. | "\color{magenta} text" |
\color[rgb]{specifier} | Custom font color — Replace
| "\color[rgb]{0,0.5,0.5} text" |
This table lists the supported special characters for the
"tex" interpreter.
| Character Sequence | Symbol | Character Sequence | Symbol | Character Sequence | Symbol |
|---|---|---|---|---|---|
| α |
| υ |
| ~ |
| ∠ |
| ϕ |
| ≤ |
|
|
| χ |
| ∞ |
| β |
| ψ |
| ♣ |
| γ |
| ω |
| ♦ |
| δ |
| Γ |
| ♥ |
| ϵ |
| Δ |
| ♠ |
| ζ |
| Θ |
| ↔ |
| η |
| Λ |
| ← |
| θ |
| Ξ |
| ⇐ |
| ϑ |
| Π |
| ↑ |
| ι |
| Σ |
| → |
| κ |
| ϒ |
| ⇒ |
| λ |
| Φ |
| ↓ |
| µ |
| Ψ |
| º |
| ν |
| Ω |
| ± |
| ξ |
| ∀ |
| ≥ |
| π |
| ∃ |
| ∝ |
| ρ |
| ∍ |
| ∂ |
| σ |
| ≅ |
| • |
| ς |
| ≈ |
| ÷ |
| τ |
| ℜ |
| ≠ |
| ≡ |
| ⊕ |
| ℵ |
| ℑ |
| ∪ |
| ℘ |
| ⊗ |
| ⊆ |
| ∅ |
| ∩ |
| ∈ |
| ⊇ |
| ⊃ |
| ⌈ |
| ⊂ |
| ∫ |
| · |
| ο |
| ⌋ |
| ¬ |
| ∇ |
| ⌊ |
| x |
| ... |
| ⊥ |
| √ |
| ´ |
| ∧ |
| ϖ |
| ∅ |
| ⌉ |
| 〉 |
| | |
| ∨ |
| 〈 |
| © |
LaTeX Markup
To use LaTeX markup, set the TickLabelInterpreter property to
'latex'. Use dollar symbols around the labels, for example, use
'$\int_1^{20} x^2 dx$' for inline mode or '$$\int_1^{20} x^2
dx$$' for display mode.
The displayed text uses the default LaTeX font style. The FontName,
FontWeight, and FontAngle properties do not have
an effect. To change the font style, use LaTeX markup within the text. The maximum size of
the text that you can use with the LaTeX interpreter is 1200 characters. For multiline text,
the maximum size of the text reduces by about 10 characters per line.
MATLAB supports most standard LaTeX math mode commands. For more information, see Supported LaTeX Commands. For examples that use TeX and LaTeX, see Greek Letters and Special Characters in Chart Text.
Tick label rotation, specified as a numeric value in degrees. Positive values give counterclockwise rotation. Negative values give clockwise rotation.
Example: ax.XTickLabelRotation = 45
Example: ax.YTickLabelRotation = 90
Alternatively, use the xtickangle, ytickangle, and ztickangle
functions.
Selection mode for the tick label rotation, specified as one of these values:
'auto'— Automatically select the tick label rotation.'manual'— Use a tick label rotation that you specify. To specify the rotation, set theXTickLabelRotation,YTickLabelRotation, orZTickLabelRotationproperty.
Minor tick marks, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0
(false). A value of 'on' is
equivalent to true, and 'off' is
equivalent to false. Thus, you can use the value of this
property as a logical value. The value is stored as an on/off logical value
of type matlab.lang.OnOffSwitchState.
'on'— Display minor tick marks between the major tick marks on the axis. The space between the major tick marks determines the number of minor tick marks. This value is the default for an axis with a log scale.'off'— Do not display minor tick marks. This value is the default for an axis with a linear scale.
Example: ax.XMinorTick = 'on'
Tick mark direction, specified as one of these values:
'in'— Direct the tick marks inward from the axis lines. (Default for 2-D views)'out'— Direct the tick marks outward from the axis lines. (Default for 3-D views)'both'— Center the tick marks over the axis lines.'none'— Do not display any tick marks.
Selection mode for the TickDir property,
specified as one of these values:
'auto'— Automatically select the tick direction based on the current view.'manual'— Manually specify the tick direction. To specify the tick direction, set theTickDirproperty.
Example: ax.TickDirMode = 'auto'
Tick mark length, specified as a two-element vector of the form
[2Dlength 3Dlength]. The first element is the tick
mark length in 2-D views and the second element is the tick mark length in
3-D views. Specify the values in units normalized relative to the longest of
the visible x-axis, y-axis, or
z-axis lines.
Example: ax.TickLength = [0.02 0.035]
Rulers
Minimum and maximum limits, specified as a two-element vector of the form
[min max], where max is greater than
min. You can specify the limits as numeric, categorical,
datetime, or duration values. However, the type of values that you specify must match
the type of values along the axis.
You can specify both limits, or specify one limit and let MATLAB automatically calculate the other. For an automatically calculated minimum
or maximum limit, use -inf or inf, respectively.
MATLAB uses the 'tight' limit method to calculate the
corresponding limit.
Example: ax.XLim = [0 10]
Example: ax.YLim = [-inf 10]
Example: ax.ZLim = [0 inf]
Alternatively, use the xlim, ylim, and zlim functions to set the limits. For an
example, see Specify Axis Limits.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | datetime | duration
Selection mode for the axis limits, specified as one of these values:
'auto'— Enable automatic limit selection, which is based on the total span of the plotted data and the value of theXLimitMethod,YLimitMethod, orZLimitMethodproperty.'manual'— Manually specify the axis limits. To specify the axis limits, set theXLim,YLim, orZLimproperty.
Example: ax.XLimMode = 'auto'
Axis limit selection method, specified as a value from the table. The examples in the table show the approximate appearance for different values of the XLimitMethod property. Your results might differ depending on your data, the size of the axes, and the type of plot you create.
| Value | Description | Example (XLimitMethod) |
|---|---|---|
'tickaligned' | In general, align the edges of the axes box with the tick marks that are closest to your data without excluding any data. The appearance might vary depending on the type of data you plot and the type of chart you create. |
|
'tight' | Fit the axes box tightly around the data by setting the axis limits equal to the range of the data. |
|
'padded' | Fit the axes box around the data with a thin margin of padding on each side. The width of the margin is approximately 7% of your data range. |
|
Note
The axis limit method has no effect when the corresponding mode property (XLimMode, YLimMode, or ZLimMode) is set to 'manual'.
Axis ruler, returned as a ruler object. The ruler controls the appearance and behavior of the x-axis, y-axis, or z-axis. Modify the appearance and behavior of a particular axis by accessing the associated ruler and setting ruler properties. The type of ruler that MATLAB creates for each axis depends on the plotted data. For a list of ruler properties, see:
For example, access the ruler for the x-axis through
the XAxis property. Then, change the
Color property of the ruler, and thus the color of
the x-axis, to red. Similarly, change the color of the
y-axis to
green.
ax = gca; ax.XAxis.Color = 'r'; ax.YAxis.Color = 'g';
Axes object has two y-axes, then the
YAxis property stores two ruler objects.x-axis location, specified as one of the values in this table. This property applies only to 2-D views.
| Value | Description | Result |
|---|---|---|
'bottom' | Bottom of the axes. Example:
|
|
'top' | Top of the axes. Example:
|
|
'origin' | Through the origin point (0,0). Example:
|
|
y-axis location, specified as one of the values in this table. This property applies only to 2-D views.
| Value | Description | Result |
|---|---|---|
'left' | Left side of the axes. Example:
|
|
'right' | Right side of the axes. Example:
|
|
'origin' | Through the origin point (0,0). Example:
|
|
Color of the axis line, tick values, and labels in the
x, y, or
z direction, specified as an RGB triplet, a
hexadecimal color code, a color name, or a short name. The color also
affects the grid lines, unless you specify the grid line color using the
GridColor or MinorGridColor
property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Example: ax.XColor = [1 1 0]
Example: ax.YColor = 'yellow'
Example: ax.ZColor = '#FFFF00'
Property for setting the x-axis grid color, specified
as 'auto' or 'manual'. The mode value
only affects the x-axis grid color. The
x-axis line, tick values, and labels always use the
XColor value, regardless of the mode.
The x-axis grid color depends on both the
XColorMode property and the
GridColorMode property, as shown
here.
| XColorMode | GridColorMode | x-Axis Grid Color |
|---|---|---|
'auto' | 'auto' | GridColor property |
'manual' | GridColor property | |
'manual' | 'auto' | XColor property |
'manual' | GridColor property |
The x-axis minor grid color depends on both the
XColorMode property and the
MinorGridColorMode property, as shown
here.
| XColorMode | MinorGridColorMode | x-Axis Minor Grid Color |
|---|---|---|
'auto' | 'auto' | MinorGridColor property |
'manual' | MinorGridColor property | |
'manual' | 'auto' | XColor property |
'manual' | MinorGridColor property |
Property for setting the y-axis grid color, specified
as 'auto' or 'manual'. The mode value
only affects the y-axis grid color. The
y-axis line, tick values, and labels always use the
YColor value, regardless of the mode.
The y-axis grid color depends on both the
YColorMode property and the
GridColorMode property, as shown
here.
| YColorMode | GridColorMode | y-Axis Grid Color |
|---|---|---|
'auto' | 'auto' | GridColor property |
'manual' | GridColor property | |
'manual' | 'auto' | YColor property |
'manual' | GridColor property |
The y-axis minor grid color depends on both the
YColorMode property and the
MinorGridColorMode property, as shown
here.
| YColorMode | MinorGridColorMode | y-Axis Minor Grid Color |
|---|---|---|
'auto' | 'auto' | MinorGridColor property |
'manual' | MinorGridColor property | |
'manual' | 'auto' | YColor property |
'manual' | MinorGridColor property |
Property for setting the z-axis grid color, specified
as 'auto' or 'manual'. The mode value
only affects the z-axis grid color. The
z-axis line, tick values, and labels always use the
ZColor value, regardless of the mode.
The z-axis grid color depends on both the
ZColorMode property and the
GridColorMode property, as shown
here.
| ZColorMode | GridColorMode | z-Axis Grid Color |
|---|---|---|
'auto' | 'auto' | GridColor property |
'manual' | GridColor property | |
'manual' | 'auto' | ZColor property |
'manual' | GridColor property |
The z-axis minor grid color depends on both the
ZColorMode property and the
MinorGridColorMode property, as shown
here.
| ZColorMode | MinorGridColorMode | z-Axis Minor Grid Color |
|---|---|---|
'auto' | 'auto' | MinorGridColor property |
'manual' | MinorGridColor property | |
'manual' | 'auto' | ZColor property |
'manual' | MinorGridColor property |
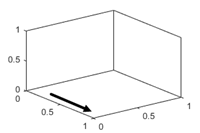
x-axis direction, specified as one of these values.
| Value | Description | Result in 2-D | Result in 3-D |
|---|---|---|---|
'normal' | Values increase from left to right. Example:
|
|
|
'reverse' | Values increase from right to left. Example:
|
|
|
y-axis direction, specified as one of these values.
| Value | Description | Result in 2-D | Result in 3-D |
|---|---|---|---|
'normal' | Values increase from bottom to top (2-D view) or front to back (3-D view). Example:
|
|
|
'reverse' | Values increase from top to bottom (2-D view) or back to front (3-D view). Example:
|
|
|
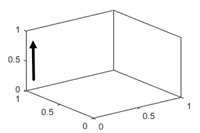
z-axis direction, specified as one of these values.
| Value | Description | Result in 3-D |
|---|---|---|
'normal' | Values increase pointing out of the screen (2-D view) or from bottom to top (3-D view). Example:
|
|
'reverse' | Values increase pointing into the screen (2-D view) or from top to bottom (3-D view). Example:
|
|
Axis scale, specified as one of these values.
| Value | Description | Result |
|---|---|---|
'linear' | Linear scale Example:
|  |
'log' | Log scale Example:
Note The axes might exclude coordinates in some cases:
|  |
Grids
Grid lines, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0
(false). A value of 'on' is
equivalent to true, and 'off' is
equivalent to false. Thus, you can use the value of this
property as a logical value. The value is stored as an on/off logical value
of type matlab.lang.OnOffSwitchState.
'on'— Display grid lines perpendicular to the axis; for example, along lines of constant x, y, or z values.'off'— Do not display the grid lines.
Alternatively, use the grid on or grid
off command to set all three properties to
'on' or 'off', respectively. For
more information, see grid.
Example: ax.XGrid = 'on'
Placement of grid lines and tick marks in relation to graphic objects, specified as one of these values:
'bottom'— Display tick marks and grid lines under graphics objects.'top'— Display tick marks and grid lines over graphics objects.
This property affects only 2-D views.
Example: ax.Layer = 'top'
Line style for grid lines, specified as one of the line styles in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
"none" | No line | No line |
To display the grid lines, use the grid on command or
set the XGrid, YGrid, or
ZGrid property to 'on'.
Example: ax.GridLineStyle = '--'
Since R2023a
Grid line width, specified as a positive number. Set this property or the MinorGridLineWidth property to control the thickness of the grid lines independently of the box outline and tick marks.
Example
Create vectors x and y, and plot them. Display the grid
lines in the axes by calling grid on. Increase the thickness of
the grid lines, box outline, and tick marks by setting the
LineWidth property of the axes to
1.5.
x = linspace(0,10);
y = sin(x);
plot(x,y)
grid on
ax = gca;
ax.LineWidth = 1.5;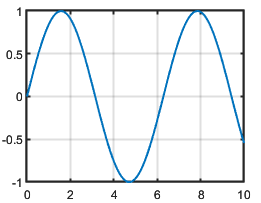
Make the grid lines thinner by setting the grid line width to 0.5.
ax.GridLineWidth = 0.5;
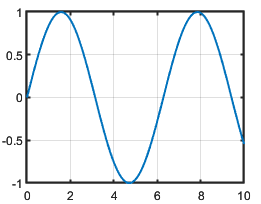
Since R2023a
How the grid line width is set, specified as one of these values:
"auto"— Set theGridLineWidthproperty to the same value as theLineWidthproperty."manual"— Hold the current value of theGridLineWidthproperty.
MATLAB sets this property to "manual" when you explicitly set
the GridLineWidth property to a value.
Color of grid lines, specified as an RGB triplet, a hexadecimal color code, a color name, or a short name.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
To set the colors for the axes box outline, use the
XColor, YColor, and
ZColor properties.
To display the grid lines, use the grid on command or
set the XGrid, YGrid, or
ZGrid property to 'on'.
Example: ax.GridColor = [0 0 1]
Example: ax.GridColor = 'blue'
Example: ax.GridColor = '#0000FF'
Property for setting the grid color, specified as one of these values:
'auto'— Check the values of theXColorMode,YColorMode, andZColorModeproperties to determine the grid line colors for the x, y, and z directions.'manual'— UseGridColorto set the grid line color for all directions.
Grid-line transparency, specified as a value in the range [0,1].
A value of 1 means opaque and a value of 0 means
completely transparent.
Example: ax.GridAlpha = 0.5
Selection mode for the GridAlpha property,
specified as one of these values:
'auto'— Default transparency value of0.15.'manual'— Manually specify the transparency value. To specify the value, set theGridAlphaproperty.
Example: ax.GridAlphaMode = 'auto'
Minor grid lines, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0
(false). A value of 'on' is
equivalent to true, and 'off' is
equivalent to false. Thus, you can use the value of this
property as a logical value. The value is stored as an on/off logical value
of type matlab.lang.OnOffSwitchState.
'on'— Display grid lines aligned with the minor tick marks of the axis. You do not need to enable minor ticks to display minor grid lines.'off'— Do not display grid lines.
Alternatively, use the grid minor command to toggle the
visibility of the minor grid lines.
Example: ax.XMinorGrid = 'on'
Line style for minor grid lines, specified as one of the line styles shown in this table.
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
"none" | No line | No line |
To display minor grid lines, use the grid minor command
or set the XMinorGrid, YMinorGrid,
or ZMinorGrid property to
'on'.
Example: ax.MinorGridLineStyle = '-.'
Since R2023a
Minor grid line width, specified as a positive number. Set this
property or the GridLineWidth property to control the thickness of the grid lines
independently of the box outline and tick marks.
Tip
To see the minor grid lines, set the
XMinorGrid,YMinorGrid, orZMinorGridproperties to"on".When you set the
GridLineWidthproperty, MATLAB also sets theMinorGridLineWidthproperty to the same value. To avoid changing theMinorGridLineWidthproperty, set theMinorGridLineWidthModeproperty to"manual"before setting theGridLineWidthproperty.
Since R2023a
How the minor grid line width is set, specified as one of these values:
"auto"— Set theMinorGridLineWidthproperty to the same value as theGridLineWidthproperty."manual"— Hold the current value of theMinorGridLineWidthproperty.
MATLAB sets this property to "manual" when you explicitly set
the MinorGridLineWidth property to a value.
Color of minor grid lines, specified as an RGB triplet, a hexadecimal color code, a color name, or a short name.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
To display minor grid lines, use the grid minor command
or set the XMinorGrid, YMinorGrid,
or ZMinorGrid property to
'on'.
Example: ax.MinorGridColor = [0 0 1]
Example: ax.MinorGridColor = 'blue'
Example: ax.MinorGridColor = '#0000FF'
Property for setting the minor grid color, specified as one of these values:
'auto'— Check the values of theXColorMode,YColorMode, andZColorModeproperties to determine the grid line colors for the x, y, and z directions.'manual'— UseMinorGridColorto set the minor grid line color for all directions.
Minor grid line transparency, specified as a value in the range [0,1].
A value of 1 means opaque and a value of 0 means
completely transparent.
Example: ax.MinorGridAlpha = 0.5
Selection mode for the MinorGridAlpha property,
specified as one of these values:
'auto'— Default transparency value of0.25.'manual'— Manually specify the transparency value. To specify the value, set theMinorGridAlphaproperty.
Example: ax.MinorGridAlphaMode = 'auto'
Labels
Text object for axes title. To add a title, set the
String property of the text object. To change the
title appearance, such as the font style or color, set other properties. For
a complete list, see Text Properties.
ax = uiaxes; ax.Title.String = 'My Graph Title'; ax.Title.FontWeight = 'normal';
Alternatively, use the title function to add a
title and control the
appearance.
title(ax,'My Title','FontWeight','normal')
Text object for the axes subtitle. To add a subtitle, set the
String property of the text object. To change its
appearance, such as the font angle, set other properties. For a complete
list, see Text Properties.
ax = uiaxes; ax.Subtitle.String = 'An Insightful Subtitle'; ax.Subtitle.FontAngle = 'italic';
Alternatively, use either the subtitle function or the title function to add a
subtitle and control the
appearance.
% subtitle function subtitle(ax,'Insightful Subtitle','FontAngle','italic') % title function [t,s] = title(ax,'Clever Title','Insightful Subtitle'); s.FontAngle = 'italic';
Note
This text object is not contained in the Children
property of the UIAxes object. It cannot be returned
by findobj, and it does not
use the default values defined for text objects.
Title and subtitle horizontal alignment with the plot box, specified as one of the values from the table.
TitleHorizontalAlignment Value | Description | Appearance |
|---|---|---|
'center' | The title and subtitle are centered over the plot box. |
|
'left' | The title and subtitle are aligned with the left side of the plot box. |
|
'right' | The title and subtitle are aligned with the right side of the plot box. |
|
Text object for axis label. To add an axis label, set the
String property of the text object. To change the
label appearance, such as the font size, set other properties. For a
complete list, see Text Properties.
ax = uiaxes;
ax.YLabel.String = 'y-Axis Label';
ax.YLabel.FontSize = 12;Alternatively, use the xlabel, ylabel, and zlabel functions to add an
axis label and control the
appearance.
ylabel(ax,'My y-Axis Label','FontSize',12)
This property is read-only.
Legend associated with the UIAxes object, specified as a
Legend object. To add a legend to the axes, use the
legend function. Then, you
can use this property to modify the legend. For a complete list of
properties, see Legend Properties.
ax = uiaxes;
ax.Legend.TextColor = 'red';You also can use this property to determine if the axes has a legend.
ax = uiaxes; lgd = ax.Legend if ~isempty(lgd) disp('Legend Exists') end
Multiple Plots
Color order, specified as a three-column matrix of RGB triplets. This property defines
the palette of colors MATLAB uses to create plot objects such as Line,
Scatter, and Bar objects. Each row of the
array is an RGB triplet. An RGB triplet is a three-element vector whose elements specify
the intensities of the red, green, and blue components of a color. The intensities must
be in the range [0, 1]. This table lists the default colors.
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
MATLAB assigns colors to objects according to their order of creation. For example, when plotting lines, the first line uses the first color, the second line uses the second color, and so on. If there are more lines than colors, then the cycle repeats.
Changing the Color Order Before or After Plotting
You can change the color order in either of the following ways:
Call the
colororderfunction to change the color order for all the axes in a figure. This function provides several predefined color palettes to choose from. When you call this function, the colors of existing plots in the figure update immediately. If you place additional axes into the figure, those axes also use the new color order. If you continue to call plotting commands, those commands also use the new colors.Set the
ColorOrderproperty on the axes, call theholdfunction to set the axes hold state to'on', and then call the desired plotting functions. This is like calling thecolororderfunction, but in this case you are setting the color order for the specific axes, not the entire figure. Setting theholdstate to'on'is necessary to ensure that subsequent plotting commands do not reset the axes to use the default color order.
Color order index, specified as a positive integer. This property specifies the next
color MATLAB selects from the axes ColorOrder property when
it creates the next plot object such as a Line,
Scatter, or Bar object.
Note
Setting the SeriesIndex property of individual plot objects
is recommended over setting the ColorOrderIndex property of the
axes. The behavior of the ColorOrderIndex property changed in
R2019b. For more information, see Indexing scheme for ColorOrder and LineStyleOrder might change plot colors and line styles.
Line style order, specified as a character vector, a cell array of character vectors,
or a string array. This property lists the line styles that MATLAB uses to display multiple plot lines in the axes. MATLAB assigns styles to lines according to their order of creation. By default,
it changes to the next line style only after cycling through all the colors in the
ColorOrder property with
the current line style. Set the LineStyleCyclingMethod
property to "withcolor" to cycle through both together or to
"beforecolor" to cycle through the line styles first. The default
LineStyleOrder has only one line style,
"-".
To customize the line style order, create a cell array of character vectors or a
string array. Specify each element of the array as a line specifier or marker specifier
from the following tables. You can combine a line and a marker specifier into a single
element, such as "-*".
| Line Style | Description | Resulting Line |
|---|---|---|
"-" | Solid line |
|
"--" | Dashed line |
|
":" | Dotted line |
|
"-." | Dash-dotted line |
|
| Marker | Description | Resulting Marker |
|---|---|---|
"o" | Circle |
|
"+" | Plus sign |
|
"*" | Asterisk |
|
"." | Point |
|
"x" | Cross |
|
"_" | Horizontal line |
|
"|" | Vertical line |
|
"square" | Square |
|
"diamond" | Diamond |
|
"^" | Upward-pointing triangle |
|
"v" | Downward-pointing triangle |
|
">" | Right-pointing triangle |
|
"<" | Left-pointing triangle |
|
"pentagram" | Pentagram |
|
"hexagram" | Hexagram |
|
Changing Line Style Order Before or After Plotting
You can change the line style order before or after plotting into the axes. When
you set the LineStyleOrder property to a new value, MATLAB updates the styles of any lines that are in the axes. If you continue
plotting into the axes, your plotting commands continue using the line styles from
the updated list.
Since R2023a
How to cycle through the line styles when there are multiple lines in the axes, specified as one of the values from this table.
The examples in this table were created using the default colors in the
ColorOrder property and three line styles
(["-","-o","--"]) in the LineStyleOrder
property.
| Value | Description | Example |
|---|---|---|
| Cycle through the line styles of the |
|
"beforecolor" | Cycle through the line styles of the
|
|
"withcolor" | Cycle through the line styles of the
|
|
This property is read-only.
SeriesIndex value for the next plot object added to the axes,
returned as a whole number greater than or equal to 0. This property
is useful when you want to track how the objects cycle through the colors and line
styles. This property maintains a count of the objects in the axes that have a numeric
SeriesIndex property value. MATLAB uses it to assign a SeriesIndex value to each new
object. The count starts at 1 when you create the axes, and it
increases by 1 for each additional object. Thus, the count is
typically n+1, where n is the number of objects in
the axes.
If you manually change the ColorOrderIndex or
LineStyleOrderIndex property on the axes, the value of the
NextSeriesIndex property changes to 0. As a
consequence, objects that have a SeriesIndex property no longer
update automatically when you change the ColorOrder or
LineStyleOrder properties on the axes.
Properties to reset when adding a new plot to the axes, specified as one of these values:
'add'— Add new plots to the existing axes. Do not delete existing plots or reset axes properties before displaying the new plot.'replacechildren'— Delete existing plots before displaying the new plot. Reset theColorOrderIndexandLineStyleOrderIndexproperties to1, but do not reset other axes properties. The next plot added to the axes uses the first color and line style based on theColorOrderandLineStyleorder properties. This value is similar to usingclabefore every new plot.'replace'— Delete existing plots and reset axes properties, exceptPositionandUnits, to their default values before displaying the new plot.'replaceall'— Delete existing plots and reset axes properties, exceptPositionandUnits, to their default values before displaying the new plot. This value is similar to usingcla resetbefore every new plot.
Note
For
UIAxesobjects with only one y-axis, the'replace'and'replaceall'property values are equivalent. ForAxesobjects with two y-axes, the'replace'value affects only the active side while the'replaceall'value affects both sides.Passing a
UIAxesobject to theclafunction with the'reset'option sets theNextPlotproperty to'replace'unless you define a different default for theNextPlotproperty.
Figures created with the uifigure function also have
a NextPlot property. Alternatively, you can use the
newplot function to
prepare figures and axes for subsequent graphics commands.
Order for rendering objects, specified as one of these values:
'depth'— Draw objects in back-to-front order based on the current view. Use this value to ensure that objects in front of other objects are drawn correctly.'childorder'— Draw objects in the order in which they are created by graphics functions, without considering the relationship of the objects in three dimensions. This value can result in faster rendering, particularly if the figure is very large, but also can result in improper depth sorting of the objects displayed.
Line style order index, specified as a positive integer. This property specifies the
next line style MATLAB selects from the axes LineStyleOrder property
to create the next plot line.
Note
Setting the SeriesIndex property of individual plot objects
is recommended over setting the LineStyleOrderIndex property of
the axes. The behavior of the LineStyleOrderIndex property
changed in R2019b. For more information, see Indexing scheme for ColorOrder and LineStyleOrder might change plot colors and line styles.
Color and Transparency Maps
Color map, specified as an m-by-3 array of RGB (red, green, blue) triplets that define m individual colors.
Example: ax.Colormap = [1 0 1; 0 0 1; 1 1 0] sets the color map to three colors: magenta, blue, and yellow.
MATLAB accesses these colors by their row number.
Alternatively, use the colormap function to change the color map.
Scale for color mapping, specified as one of these values:
'linear'— Linear scale. The tick values along the colorbar also use a linear scale.'log'— Log scale. The tick values along the colorbar also use a log scale.
Color limits for objects in axes that use the colormap, specified as a
two-element vector of the form [cmin cmax]. This property
determines how data values map to the colors in the colormap where:
cminspecifies the data value that maps to the first color in the colormap.cmaxspecifies the data value that maps to the last color in the colormap.
The Axes object interpolates data values
between cmin and cmax across the
colormap. Values outside this range use either the first or last color,
whichever is closest.
Selection mode for the CLim property, specified
as one of these values:
'auto'— Automatically select the limits based on the color data of the graphics objects contained in the axes.'manual'— Manually specify the values. To specify the values, set theCLimproperty. The values do not change when the limits of the axes children change.
Transparency map, specified as an array of finite alpha values that progress linearly from
0 to 1. The size of the array can be
m-by-1 or 1-by-m. MATLAB accesses alpha values by their index in the array. An alphamap can be any
length.
Scale for transparency mapping, specified as one of these values:
'linear'— Linear scale'log'— Log scale
Alpha limits, specified as a two-element vector of the form [amin
amax]. This property affects the
AlphaData values of graphics objects, such as
surface, image, and patch objects. This property determines how the
AlphaData values map to the figure alpha map,
where:
aminspecifies the data value that maps to the first alpha value in the figure alpha map.amaxspecifies the data value that maps to the last alpha value in the figure alpha map.
The UIAxes object interpolates data values between
amin and amax across the figure
alpha map. Values outside this range use either the first or last alpha map
value, whichever is closest.
The Alphamap property
of the figure contains the alpha map. For more information, see the
alpha function.
Selection mode for the ALim property, specified
as one of these values:
'auto'— Automatically select the limits based on theAlphaDatavalues of the graphics objects contained in the axes.'manual'— Manually specify the alpha limits. To specify the alpha limits, set theALimproperty.
Box Styling
Color of plot area, specified as an RGB triplet, a hexadecimal color code,
a color name, or a short name. The color affects the area defined by the
InnerPosition property value.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Example: ax.Color = [0 0 1]
Example: ax.Color = 'blue'
Example: ax.Color = '#0000FF'
Color of margin around plot area, returned as 'none'.
Note
Setting this property has no effect.
Line width of axes outline, tick marks, and grid lines, specified as a positive numeric value in point units. One point equals 1/72 inch.
Example: ax.LineWidth = 1.5
Box outline, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0
(false). A value of 'on' is
equivalent to true, and 'off' is
equivalent to false. Thus, you can use the value of this
property as a logical value. The value is stored as an on/off logical value
of type matlab.lang.OnOffSwitchState.
| Value | Description | 2-D Result | 3-D Result |
|---|---|---|---|
'on' | Display the box outline around the axes. For
3-D views, use the Example:
|
|
|
'off' | Do not display the box outline around the axes. Example:
|
|
|
The XColor,
YColor, and ZColor properties
control the color of the outline.
Example: ax.Box = 'on'
Box outline style, specified as 'back' or
'full'. This property affects only 3-D views.
| Value | Description | Result |
|---|---|---|
'back' | Outline the back planes of the 3-D box. Example:
|
|
'full' | Outline the entire 3-D box. Example:
|
|
Clipping of objects to the axes limits, specified as
'on' or 'off', or as numeric or
logical 1 (true) or
0 (false). A value of
'on' is equivalent to true, and
'off' is equivalent to false.
Thus, you can use the value of this property as a logical value. The value
is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
The clipping behavior of an object within the Axes object depends on both the Clipping
property of the Axes object and the
Clipping property of the individual object. The
property value of the Axes object has
these effects:
'on'— Enable each individual object within the axes to control its own clipping behavior based on theClippingproperty value for the object.'off'— Disable clipping for all objects within the axes, regardless of theClippingproperty value for the individual objects. Parts of objects can appear outside of the axes limits. For example, parts can appear outside the limits if you create a plot, use thehold oncommand, freeze the axis scaling, and then add a plot that is larger than the original plot.
This table lists the results for different combinations of
Clipping property values.
| Clipping Property for Axes Object | Clipping Property for Individual Object | Result |
|---|---|---|
'on' | 'on' | Individual object is clipped. Others might or might not be. |
'on' | 'off' | Individual object is not clipped. Others might or might not be. |
'off' | 'on' | All objects are unclipped. |
'off' | 'off' | All objects are unclipped. |
Clipping boundaries, specified as one of the values in this table. If a plot contains markers, then as long as the data point lies within the axes limits, MATLAB draws the entire marker.
The ClippingStyle property has no effect if the
Clipping property is set to
'off'.
| Value | Descriptions | Illustration of Boundary Region |
|---|---|---|
'3dbox' | Clip plotted objects to the six sides of the axes box defined by the axis limits. Thick lines might display outside the axes limits. |
|
'rectangle' | Clip plotted objects to a rectangular boundary enclosing the axes in any given view. Clip thick lines at the axes limits. |
|
Background light color, specified as an RGB triplet, a hexadecimal color
code, a color name, or a short name. The background light is a directionless
light that shines uniformly on all objects in the axes. To add light, use
the light function.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
This table lists the default color palettes for plots in the light and dark themes.
| Palette | Palette Colors |
|---|---|
Before R2025a: Most plots use these colors by default. |
|
|
|
You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.
RGB = orderedcolors("gem");
H = rgb2hex(RGB);Before R2023b: Get the RGB triplets using RGB =
get(groot,"FactoryAxesColorOrder").
Before R2024a: Get the hexadecimal color codes using H =
compose("#%02X%02X%02X",round(RGB*255)).
Example: ax.AmbientLightColor = [1 0 1]
Example: ax.AmbientLightColor = 'magenta'
Example: ax.AmbientLightColor = '#FF00FF'
Position
Size and location of axes, including the labels and margins, specified as a four-element
vector of the form [left bottom width height]. This property is
equivalent to the OuterPosition property. The vector defines a
rectangle that encloses the outer bounds of the axes. The values are measured in the
units specified by the Units property, which defaults to pixels.
The
leftandbottomelements define the position of the rectangle, measured from the lower left corner of the parent container.The
widthandheightdefine the size of the rectangle.
If you want to specify the position and account for the text around the axes, then set
the either the Position or the OuterPosition
property. These figures show the areas defined by the Position (or
OuterPosition) in blue, and the
InnerPosition in red.
| 2-D View of Axes | 3-D View of Axes |
|---|---|
|
|
Note
Setting this property has no effect when the parent container is a
TiledChartLayout object.
Inner size and location, excluding labels and margins, specified as a
four-element vector of the form [left bottom width
height]. The values are measured in the units specified by the
Units property, which defaults to pixels.
The
leftandbottomelements define the position of the rectangle, measured from the lower left corner of the parent container.The
widthandheightdefine the size of the rectangle.
If you want to specify the position and account for the text around the
axes, then set the either the Position or the
OuterPosition property. These figures show the
areas defined by the Position (or
OuterPosition) in blue, and the
InnerPosition in red.
| 2-D View of Axes | 3-D View of Axes |
|---|---|
|
|
MATLAB automatically sets InnerPosition to the
largest possible values that conform to all other properties. Other UIAxes properties that affect the axes size and
shape include Position,
DataAspectRatio and
PlotBoxAspectRatio.
Note
When querying the inner position of axes with constrained aspect ratios (such as square axes or those containing images) consider using the
tightPositionfunction for more accuracy. (since R2022b)Setting this property has no effect when the parent container is a
TiledChartLayout
Size and location of the axes, including the labels and margins, specified
as a four-element vector of the form [left bottom width
height].
This property value is identical to the Position
property value.
This property is read-only.
Margin for text labels, returned as a four-element vector of the form
[left bottom right top]. The elements define the
distances between the bounds of the InnerPosition
property and the extent of the axes text labels and title. By default, the
values are measured in pixels. To change the units, set the
Units property.
Position property to hold constant when adding, removing, or changing decorations, specified as one of the following values:
"outerposition"— TheOuterPositionproperty remains constant when you add, remove, or change decorations such as a title or an axis label. If any positional adjustments are needed, MATLAB adjusts theInnerPositionproperty."innerposition"— TheInnerPositionproperty remains constant when you add, remove, or change decorations such as a title or an axis label. If any positional adjustments are needed, MATLAB adjusts theOuterPositionproperty.
Note
Setting this property has no effect when the parent container is a
TiledChartLayout object.
Position units, specified as one of these values.
Units | Description |
|---|---|
'normalized' | Normalized with respect to the container, which is
typically the figure or a panel. The lower left corner
of the container maps to (0,0) and
the upper right corner maps to
(1,1). |
'inches' | Inches. |
'centimeters' | Centimeters. |
'characters' | Based on the default uicontrol font of the graphics root object:
|
'points' | Typography points. One point equals 1/72 inch. |
'pixels' | On Windows and Macintosh systems, the size of a pixel is 1/96th of an inch. This size is independent of your system resolution. On Linux systems, the size of a pixel is determined by your system resolution. |
When specifying the units as a Name,Value pair during
object creation, you must set the Units property before
specifying the properties that you want to use these units, such as
Position.
Relative length of data units along each axis, specified as a
three-element vector of the form [dx dy dz]. This vector
defines the relative x, y, and
z data scale factors. For example, specifying this
property as [1 2 1] sets the length of one unit of data
in the x-direction to be the same length as two units of
data in the y-direction and one unit of data in the
z-direction.
Alternatively, use the daspect function to change
the data aspect ratio.
Example: ax.DataAspectRatio = [1 1 1]
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Data aspect ratio mode, specified as one of these values:
'auto'— Automatically select values that make best use of the available space. IfPlotBoxAspectRatioModeandCameraViewAngleModeare also set to'auto', then enable "stretch-to-fill" behavior. Stretch the axes so that it fills the available space as defined by thePositionproperty.'manual'— Disable the "stretch-to-fill" behavior and use the manually specified data aspect ratio. To specify the values, set theDataAspectRatioproperty.
Relative length of each axis, specified as a three-element vector of the
form [px py pz] defining the relative
x-axis, y-axis, and
z-axis scale factors. The plot box is a box
enclosing the axes data region as defined by the axis limits.
Alternatively, use the pbaspect function to
change the data aspect ratio.
If you specify the axis limits, data aspect ratio, and plot box aspect ratio, then MATLAB ignores the plot box aspect ratio. It adheres to the axis limits and data aspect ratio.
Example: ax.PlotBoxAspectRatio = [1 0.75
0.75]
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Selection mode for the PlotBoxAspectRatio property,
specified as one of these values:
'auto'— Automatically select values that make best use of the available space. IfDataAspectRatioModeandCameraViewAngleModealso are set to'auto', then enable "stretch-to-fill" behavior. Stretch theAxesobject so that it fills the available space as defined by thePositionproperty.'manual'— Disable the "stretch-to-fill" behavior and use the manually specified plot box aspect ratio. To specify the values, set thePlotBoxAspectRatioproperty.
Layout options, specified as a
GridLayoutOptions or
TiledChartLayoutOptions object. This property
specifies options when the axes is in a grid layout or a tiled chart layout.
If the axes is not in either type of layout, then this property is empty and
has no effect.
To position the axes in a specific row and column of a grid layout, set
the Row and Column properties on
the GridLayoutOptions object. For example, this code
places the axes in the third row and second column of a grid
layout.
g = uigridlayout([4 3]); ax = uiaxes(g); ax.Layout.Row = 3; ax.Layout.Column = 2;
To make the axes span multiple rows or columns, specify the
Row or Column property as a
two-element vector. For example, this axes spans columns
2 through
3:
ax.Layout.Column = [2 3];
View
Azimuth and elevation of view, specified as a two-element vector of the
form [azimuth elevation] defined in degree units.
Alternatively, use the view function to set the
view.
Note
Setting the azimuth and elevation angles might reset other camera-related properties. For best results, set the azimuth and elevation angles before setting other camera-related properties.
Example: ax.View = [45 45]
Type of projection onto a 2-D screen, specified as one of these values:
'orthographic'— Maintain the correct relative dimensions of graphics objects regarding the distance of a given point from the viewer, and draw lines that are parallel in the data parallel on the screen.'perspective'— Incorporate foreshortening, which enables you to perceive depth in 2-D representations of 3-D objects. Perspective projection does not preserve the relative dimensions of objects. Instead, it displays a distant line segment smaller than a nearer line segment of the same length. Lines that are parallel in the data might not appear parallel on screen.
Camera location, or the viewpoint, specified as a three-element vector of
the form [x y z]. This vector defines the axes
coordinates of the camera location, which is the point from which you view
the axes. The camera is oriented along the view axis, which is a straight
line that connects the camera position and the camera target. For an
illustration, see Camera Graphics Terminology.
If the Projection
property is set to 'perspective', then as you change the
CameraPosition setting, the amount of perspective
also changes.
Alternatively, use the campos function to set the
camera location.
Example: ax.CameraPosition = [0.5 0.5 9]
Data Types: single | double
Selection mode for the CameraPosition property,
specified as one of these values:
'auto'— Automatically setCameraPositionalong the view axis. Calculate the position so that the camera lies a fixed distance from the target along the azimuth and elevation specified by the current view, as returned by theviewfunction. Functions likerotate3d,zoom, andpan, change this mode to'auto'to perform their actions.'manual'— Manually specify the value. To specify the value, set theCameraPositionproperty.
Camera target point, specified as a three-element vector of the form
[x y z]. This vector defines the axes coordinates of
the point. The camera is oriented along the view axis, which is a straight
line that connects the camera position and the camera target. For an
illustration, see Camera Graphics Terminology.
Alternatively, use the camtarget function to set the
camera target.
Example: ax.CameraTarget = [0.5 0.5 0.5]
Data Types: single | double
Selection mode for the CameraTarget property,
specified as one of these values:
'auto'— Position the camera target at the centroid of the axes plot box.'manual'— Use the manually specified camera target value. To specify a value, set theCameraTargetproperty.
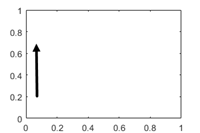
Vector defining upwards direction, specified as a three-element direction
vector of the form [x y z]. For 2-D views, the default
value is [0 1 0]. For 3-D views, the default value is
[0 0 1]. For an illustration, see Camera Graphics Terminology.
Alternatively, use the camup function to set the
upwards direction.
Example: ax.CameraUpVector = [sin(45) cos(45)
1]
Selection mode for the CameraUpVector property,
specified as one of these values:
'auto'— Automatically set the value to[0 0 1]for 3-D views so that the positive z-direction is up. Set the value to[0 1 0]for 2-D views so that the positive y-direction is up.'manual'— Manually specify the vector defining the upwards direction. To specify a value, set theCameraUpVectorproperty.
Field of view, specified as a scalar angle greater than 0 and less than or equal to 180. Changing the camera view angle affects the size of graphics objects displayed in the axes, but does not affect the degree of perspective distortion. The greater the angle, the larger the field of view and the smaller objects appear in the scene. For an illustration, see Camera Graphics Terminology.
Example: ax.CameraViewAngle = 15
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Selection mode for the CameraViewAngle property,
specified as one of these values:
'auto'— Automatically select the field of view as the minimum angle that captures the entire scene, up to 180 degrees.'manual'— Manually specify the field of view. To specify a value, set theCameraViewAngleproperty.
Interactivity
Options to customize interaction behavior, specified as a
CartesianAxesInteractionOptions object. Use the
properties of the CartesianAxesInteractionOptions object to
customize the behavior of interactions with the axes. For a complete list of
properties, see CartesianAxesInteractionOptions Properties.
Before R2024a: Specify this property as an
InteractionOptions object instead of as a
CartesianAxesInteractionOptions object.
The options set by the CartesianAxesInteractionOptions
object apply to these interactions on the associated axes:
The built-in interactions specified by the
Interactionsproperty of the axesInteractions enabled by using mode functions, such as
panandzoomInteractions enabled using the axes toolbar
Example: ax.InteractionOptions.LimitsDimensions = "x"
constrains all pan and zoom interactions to the
x-dimension.
Toolbar with individual interaction buttons, specified as an
AxesToolbar object or an empty array. Use this property
to customize the appearance and behavior of the toolbar. Create the toolbar
using the axtoolbar function. The toolbar appears at the top-right
corner of the UI axes when you hover over it.
![]()
The toolbar buttons depend on the contents of the UI axes, but typically
include zooming, panning, rotating, brushing, exporting, and restoring the
original view. You can customize the toolbar buttons using the axtoolbar and axtoolbarbtn functions.
For a complete list of properties, see AxesToolbar Properties.
To remove the toolbar, set this property to an empty array.
Built-in interactions, specified as an array of interaction objects or an empty array. These interactions are available within your chart through gestures. You do not have to select any axes toolbar buttons to use them.
The default set of built-in interactions depends on the chart type. You can replace the default set with a new set of interactions, but you cannot access or modify the default set of interactions.
To remove all interactions from the axes, set this property to an empty
array. To temporarily disable the current set of interactions, call the
disableDefaultInteractivity function. You can reenable them
by calling the enableDefaultInteractivity function.
For a list of interaction objects, see Customize Built-In Interactions.
Example: ax.Interactions = [panInteraction
zoomInteraction] replaces the default set of built-in
interactions with the panInteraction and zoomInteraction objects. This set of interactions enables
dragging to pan within the chart and scrolling to zoom within the
chart.
State of visibility, specified as 'on' or 'off', or as numeric or logical 1 (true) or 0 (false). A value of 'on' is equivalent to true, and 'off' is equivalent to false. Thus, you can use the value of this property as a logical value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
'on'— Display the axes and its children.'off'— Hide the axes without deleting it. You still can access the properties of an invisible axes object.
Note
When the Visible property is 'off', the axes
object is invisible, but child objects such as lines remain visible.
Location of mouse pointer, specified as a 2-by-3 array. The
CurrentPoint property contains the
(x,y,z)
coordinates of the mouse pointer with respect to the axes. The returned
array is of the
form:
[xfront yfront zfront xback yback zback]
The two points indicate the location of the last mouse click. However, if
the figure has a WindowButtonMotionFcn callback
defined, then the points indicate the last location of the mouse pointer.
The figure also has a CurrentPoint property.
The values of the current point when using perspective projection can be different from the same point in orthographic projection because the shape of the axes volume can be different.
Orthogonal Projection
When using orthogonal projection, the values depend on whether the click is within the axes or outside the axes.
If the click is inside the axes, the two points lie on the line that is perpendicular to the plane of the screen and that passes through the pointer. The coordinates are the points where this line intersects the front and back surfaces of the axes volume (which is defined by the axes x, y, and z limits). The first row is the point nearest to the camera position. The second row is the point farthest from the camera position. This is true for both 2-D and 3-D views.
If the click is outside the axes, but within the figure, then the points lie on a line that passes through the pointer and is perpendicular to the camera target and camera position planes. The first row is the point in the camera position plane. The second row is the point in the plane of the camera target.
Perspective Projection
Clicking outside of the UIAxes object in perspective
projection returns the front point as the current camera position. Only
the back point updates with the coordinates of a point that lies on a
line extending from the camera position through the pointer and
intersecting the camera target at that point.
Context menu, specified as a ContextMenu object. Use this property
to display a context menu when you right-click the object. Create the context menu using
the uicontextmenu function.
Note
If the PickableParts property is set to
'none' or if the HitTest property is set
to 'off', then the context menu does not appear.
Selection state, specified as 'on' or 'off', or as
numeric or logical 1 (true) or
0 (false). A value of 'on'
is equivalent to true, and 'off' is equivalent to
false. Thus, you can use the value of this property as a logical
value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
'on'— Selected. If you click the object when in plot edit mode, then MATLAB sets itsSelectedproperty to'on'. If theSelectionHighlightproperty also is set to'on', then MATLAB displays selection handles around the object.'off'— Not selected.
Display of selection handles when selected, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0 (false). A
value of 'on' is equivalent to true, and
'off' is equivalent to false. Thus, you can
use the value of this property as a logical value. The value is stored as an on/off
logical value of type matlab.lang.OnOffSwitchState.
'on'— Display selection handles when theSelectedproperty is set to'on'.'off'— Never display selection handles, even when theSelectedproperty is set to'on'.
Callbacks
Mouse-click callback, specified as one of these values:
Function handle
Cell array containing a function handle and additional arguments
Character vector that is a valid MATLAB command or function, which is evaluated in the base workspace (not recommended)
Use this property to execute code when you click the object. If you specify this property using a function handle, then MATLAB passes two arguments to the callback function when executing the callback:
Clicked object — Access properties of the clicked object from within the callback function.
Event data — Empty argument. Replace it with the tilde character (
~) in the function definition to indicate that this argument is not used.
For more information on how to use function handles to define callback functions, see Create Callbacks for Graphics Objects.
Note
If the PickableParts property is set to 'none' or
if the HitTest property is set to 'off',
then this callback does not execute.
Object creation function, specified as one of these values:
Function handle.
Cell array in which the first element is a function handle. Subsequent elements in the cell array are the arguments to pass to the callback function.
Character vector containing a valid MATLAB expression (not recommended). MATLAB evaluates this expression in the base workspace.
For more information about specifying a callback as a function handle, cell array, or character vector, see Callbacks in App Designer.
This property specifies a callback function to execute when MATLAB creates the object. MATLAB initializes all property values before executing the CreateFcn callback. If you do not specify the CreateFcn property, then MATLAB executes a default creation function.
Setting the CreateFcn property on an existing component has no effect.
If you specify this property as a function handle or cell array, you can access the object that is being created using the first argument of the callback function. Otherwise, use the gcbo function to access the object.
Object deletion function, specified as one of these values:
Function handle.
Cell array in which the first element is a function handle. Subsequent elements in the cell array are the arguments to pass to the callback function.
Character vector containing a valid MATLAB expression (not recommended). MATLAB evaluates this expression in the base workspace.
For more information about specifying a callback as a function handle, cell array, or character vector, see Callbacks in App Designer.
This property specifies a callback function to execute when MATLAB deletes the object. MATLAB executes the DeleteFcn callback before destroying the
properties of the object. If you do not specify the DeleteFcn
property, then MATLAB executes a default deletion function.
If you specify this property as a function handle or cell array, you can access the
object that is being deleted using the first argument of the callback function.
Otherwise, use the gcbo function to access the
object.
Callback Execution Control
Callback interruption, specified as 'on' or 'off', or as
numeric or logical 1 (true) or
0 (false). A value of 'on'
is equivalent to true, and 'off' is equivalent to
false. Thus, you can use the value of this property as a logical
value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
This property determines if a running callback can be interrupted. There are two callback states to consider:
The running callback is the currently executing callback.
The interrupting callback is a callback that tries to interrupt the running callback.
MATLAB determines callback interruption behavior whenever it executes a command that
processes the callback queue. These commands include drawnow, figure, uifigure, getframe, waitfor, and pause.
If the running callback does not contain one of these commands, then no interruption occurs. MATLAB first finishes executing the running callback, and later executes the interrupting callback.
If the running callback does contain one of these commands, then the
Interruptible property of the object that owns the running
callback determines if the interruption occurs:
If the value of
Interruptibleis'off', then no interruption occurs. Instead, theBusyActionproperty of the object that owns the interrupting callback determines if the interrupting callback is discarded or added to the callback queue.If the value of
Interruptibleis'on', then the interruption occurs. The next time MATLAB processes the callback queue, it stops the execution of the running callback and executes the interrupting callback. After the interrupting callback completes, MATLAB then resumes executing the running callback.
Note
Callback interruption and execution behave differently in these situations:
If the interrupting callback is a
DeleteFcn,CloseRequestFcn, orSizeChangedFcncallback, then the interruption occurs regardless of theInterruptibleproperty value.If the running callback is currently executing the
waitforfunction, then the interruption occurs regardless of theInterruptibleproperty value.If the interrupting callback is owned by a
Timerobject, then the callback executes according to schedule regardless of theInterruptibleproperty value.
Callback queuing, specified as 'queue' or 'cancel'. The BusyAction property determines how MATLAB handles the execution of interrupting callbacks. There are two callback states to consider:
The running callback is the currently executing callback.
The interrupting callback is a callback that tries to interrupt the running callback.
The BusyAction property determines callback queuing behavior only
when both of these conditions are met:
Under these conditions, the BusyAction property of the
object that owns the interrupting callback determines how MATLAB handles the interrupting callback. These are possible values of the
BusyAction property:
'queue'— Puts the interrupting callback in a queue to be processed after the running callback finishes execution.'cancel'— Does not execute the interrupting callback.
Ability to capture mouse clicks, specified as one of these values:
'visible'— Capture mouse clicks only when visible. TheVisibleproperty must be set to'on'. TheHitTestproperty determines if theUIAxesobject responds to the click or if an ancestor does.'all'— Capture mouse clicks regardless of visibility. TheVisibleproperty can be set to'on'or'off'. TheHitTestproperty determines if theUIAxesobject responds to the click or if an ancestor does.'none'— Cannot capture mouse clicks. Clicking theUIAxesobject passes the click to the object below it in the current view of the figure window, which is typically the axes or the figure. TheHitTestproperty has no effect.
If you want an object to be clickable when it is underneath
other objects that you do not want to be clickable, then set the PickableParts property
of the other objects to 'none' so that the click
passes through them.
Response to captured mouse clicks, specified as 'on' or
'off', or as numeric or logical 1
(true) or 0 (false). A
value of 'on' is equivalent to true, and 'off' is
equivalent to false. Thus, you can use the value of this property as
a logical value. The value is stored as an on/off logical value of type matlab.lang.OnOffSwitchState.
'on'— Trigger theButtonDownFcncallback of theUIAxesobject. If you have defined theContextMenuproperty, then invoke the context menu.'off'— Trigger the callbacks for the nearest ancestor of theUIAxesobject that meets one of these conditions:HitTestproperty is set to'on'.PickablePartsproperty is set to a value that enables the ancestor to capture mouse clicks.
Note
The PickableParts property determines if
the UIAxes object can capture
mouse clicks. If it cannot, then the HitTest property
has no effect.
This property is read-only.
Deletion status, returned as an on/off logical value of type matlab.lang.OnOffSwitchState.
MATLAB sets the BeingDeleted property to
'on' when the DeleteFcn callback begins
execution. The BeingDeleted property remains set to
'on' until the component object no longer exists.
Check the value of the BeingDeleted property to verify that the object is not about to be deleted before querying or modifying it.
Parent/Child
Parent container, specified as a Figure,
Panel, Tab, GridLayout, or TiledChartLayout object. If
no container is specified, MATLAB calls the uifigure function to create a
new Figure object that serves as the
parent container.
Children, returned as an array of graphics objects. Use this property to view a list of the children or to reorder the children by setting the property to a permutation of itself.
You cannot add or remove children using the Children property.
To add a child to this list, set the Parent property
of the child graphics object to the UIAxes object.
Visibility of the object handle in the Children property
of the parent, specified as one of these values:
"on"— Object handle is always visible."off"— Object handle is invisible at all times. This option is useful for preventing unintended changes by another function. SetHandleVisibilityto"off"to temporarily hide the handle during the execution of that function."callback"— Object handle is visible from within callbacks or functions invoked by callbacks, but not from within functions invoked from the command line. This option blocks access to the object at the command line, but permits callback functions to access it.
If the object is not listed in the Children property of the parent, then
functions that obtain object handles by searching the object hierarchy or querying
handle properties cannot return it. Examples of such functions include the
get, findobj, gca, gcf, gco, newplot, cla, clf, and close functions.
Hidden object handles are still valid. Set the root ShowHiddenHandles
property to "on" to list all object handles regardless of their
HandleVisibility property setting.
Identifiers
This property is read-only.
Type of graphics object returned as 'axes'.
Object identifier, specified as a character vector or string scalar. You can specify a unique Tag value to serve as an identifier for an object. When you need access to the object elsewhere in your code, you can use the findobj function to search for the object based on the Tag value.
User data, specified as any MATLAB array. For example, you can specify a scalar, vector, matrix, cell array, character array, table, or structure. Use this property to store arbitrary data on an object.
If you are working in App Designer, create public or private properties in the app to share data instead of using the UserData property. For more information, see Share Data Within App Designer Apps.
Version History
Introduced in R2016aThe default ColorOrder, XColor,
YColor, and ZColor property values in
the light theme have changed slightly. This table lists the changes.
| Property | R2024b Color | R2025a Color | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||||||||||||||||||||||||
XColor, YColor, and
ZColor |
|
|
The InteractionOptions object is now called
CartesianAxesInteractionOptions. The behavior remains the same.
The name of the InteractionOptions property has not changed.
Starting in R2024a, set the InteractionOptions property using a
CartesianAxesInteractionOptions object.
Use the LineStyleCyclingMethod property to control how
different lines are distinguished from one another in the axes.
Change the thickness of grid lines independently of the box outline and tick marks
by setting the GridLineWidth and
MinorGridLineWidth properties of the axes. Before R2023a,
the LineWidth property of the axes was the only property for
controlling the grid line width. However, that property controlled the grid lines,
box outline, and tick marks together. Now you can control the thickness of the grid
lines separately.
Use the InteractionOptions property to control the behavior
of axes interactions, such as pan, zoom, and rotate.
Control the selection mode for tick label rotation by setting the
XTickLabelRotationMode,
YTickLabelRotationMode, or
ZTickLabelRotationMode property.
You can remove all the tick marks from the axes by setting the
TickDir property to "none".
Control the axis limits for your plots by setting the
XLimitMethod, YLimitMethod, or
ZLimitMethod on the axes.
Setting the BackgroundColor property on a
UIAxes object no longer has any effect. Starting in R2020b,
the area around the plot box is transparent regardless of the value of the
BackgroundColor property.
To produce the same effect as setting the background color in previous releases,
create a panel with the desired BackgroundColor value, and then
place the UIAxes in the panel.
The stacking order (also called the Z-order) of objects in the figure has changed
so that UIAxes objects and their contents appear behind all UI
components in the figure. This behavior is consistent with the behavior of other
types of axes.
For example, this code creates a figure, a button, and then a
UIAxes object.
fig = uifigure; b = uibutton(fig); uax = uiaxes(fig);
In R2020a, executing the preceding code displays the UIAxes in
front of the button, as shown in the figure on the left. The figure on the right
shows the behavior in R2020b, where the UIAxes appears behind UI
components regardless of the order of creation.

The order of the objects listed in the Children property of
the figure also reflects this change. The UIAxes object is always
after UI components in the
list.
fig.Children
ans = 2×1 graphics array: Button (Button) UIAxes
Plot objects such as lines might not clip to the bounds defined by the
OuterPosition property of the UIAxes. The
lines extend beyond the bounds when the Clipping property of
each line is set to 'off'. In previous releases, the lines clip
to the OuterPosition regardless of the value of the
Clipping property. For example, the plot on the left shows
the R2020a behavior, and the plot on the right shows the R2020b behavior. In both
cases, the Clipping properties of the lines are set to
'off'.

To prevent the axes content from overlapping with components in your app, set the
Clipping property of each object in the axes to
'on'.
The SizeChangedFcn callback for UIAxes
objects has been removed. If your app requires a callback that executes when the
size of the axes changes, create a SizeChangedFCn callback for
the parent figure or another container.
When you create a plot in a UIAxes object, and then create a
colorbar or legend for that plot, the parent object of the colorbar or legend is the
same as the parent object of the UIAxes object. In previous
releases, the parent object of the colorbar or legend is the
UIAxes object.
You can control the alignment of a plot title by setting the
TitleHorizontalAlignment property of the axes to
"left", "right", or
"center".
Add a subtitle to your plot by setting the Subtitle property
or calling the subtitle function. To control the appearance of the subtitle, set
the SubtitleFontWeight property.
Set the PositionConstraint property of an
Axes object to control the space around the plot box when you
add or modify decorations such as titles and axis labels.
If you change the axes ColorOrder or
LineStyleOrder properties after plotting into the axes, the colors
and line styles in your plot update immediately. In R2019a and previous releases, the new
colors and line styles affect only subsequent plots, not the existing plots.
To preserve the original behavior, set the axes ColorOrderIndex or
LineStyleOrderIndex property to any value (such as its current
value) before changing the ColorOrder or
LineStyleOrder property.
There is a new indexing scheme that enables you to change the colors and line styles of
existing plots by setting the ColorOrder or
LineStyleOrder properties. MATLAB applies this indexing scheme to all objects that have a
ColorMode, FaceColorMode,
MarkerFaceColorMode, or CDataMode. As a
result, your code might produce plots that cycle though the colors and line styles
differently than in previous releases.
In R2019a and earlier releases, MATLAB uses a different indexing scheme which does not allow you to change the colors of existing plots.
To preserve the way your plots cycle through colors and line styles, set the axes
ColorOrderIndex or LineStyleOrderIndex
property to any value (such as its current value) before plotting into the axes.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)