TuningGoal.MaxLoopGain
Maximum loop gain constraint for control system tuning
Description
Use TuningGoal.MaxLoopGain to enforce a maximum
loop gain and desired roll-off in a particular frequency band. Use this tuning goal with control
system tuning commands such as systune or
looptune.
This tuning goal imposes a maximum gain on the open-loop frequency response (L) at a specified location in your control system. You specify the maximum open-loop gain as a function of frequency (a maximum gain profile). For MIMO feedback loops, the specified gain profile is interpreted as an upper bound on the largest singular value of L.
When you tune a control system, the maximum gain profile is converted to a maximum gain constraint on the complementary sensitivity function, T) = L/(I + L).
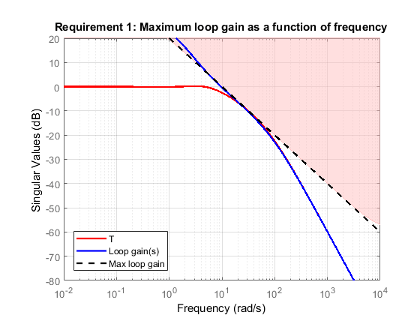
The following figure shows a typical specified maximum gain profile (dashed line) and a resulting tuned loop gain, L (blue line). The shaded region represents gain profile values that are forbidden by this tuning goal. The figure shows that when L is much smaller than 1, imposing a maximum gain on T is a good proxy for a maximum open-loop gain.
TuningGoal.MaxLoopGain and TuningGoal.MinLoopGain specify only high-gain or low-gain constraints in certain
frequency bands. When you use these tuning goals, systune and
looptune determine the best loop shape near crossover. When the loop shape
near crossover is simple or well understood (such as integral action), you can use TuningGoal.LoopShape to specify that target loop shape.
Creation
Syntax
Description
Req = TuningGoal.MaxLoopGain(location,loopgain)loopgain. You can specify the maximum gain
profile as a smooth transfer function or sketch a piecewise error profile using an
frd model or the makeweight (Robust Control Toolbox) command. Only gain values smaller than 1 are enforced.
Input Arguments
Properties
Examples
Tips
This tuning goal imposes an implicit stability constraint on the closed-loop sensitivity function measured at
Location, evaluated with loops opened at the points identified inOpenings. The dynamics affected by this implicit constraint are the stabilized dynamics for this tuning goal. TheMinDecayandMaxRadiusoptions ofsystuneOptionscontrol the bounds on these implicitly constrained dynamics. If the optimization fails to meet the default bounds, or if the default bounds conflict with other requirements, usesystuneOptionsto change these defaults.
Algorithms
When you tune a control system using a TuningGoal, the software converts
the tuning goal into a normalized scalar value f(x). Here,
x is the vector of free (tunable) parameters in the control system. The
software then adjusts the parameter values to minimize f(x)
or to drive f(x) below 1 if the tuning goal is a hard
constraint.
For TuningGoal.MaxLoopGain, f(x) is
given by:
Here, D is a diagonal scaling (for MIMO loops). T is
the complementary sensitivity function at Location.
WT is a frequency-weighting function derived from the
maximum loop gain profile, MaxGain. The gain of this function roughly matches
1/MaxGain for values ranging from –60 dB to 20 dB. For numerical reasons, the
weighting function levels off outside this range, unless the specified gain profile changes slope
outside this range. This adjustment is called regularization. Because
poles of WT close to s = 0 or
s = Inf might lead to poor numeric conditioning of the
systune optimization problem, it is not recommended to specify gain
profiles with very low-frequency or very high-frequency dynamics.
To obtain WT, use:
WT = getWeight(Req,Ts)
where Req is the tuning goal, and Ts is the sample
time at which you are tuning (Ts = 0 for continuous time). For more
information about regularization and its effects, see Visualize Tuning Goals.
Although T is a closed-loop transfer function, driving f(x) < 1 is equivalent to enforcing an upper bound on the open-loop transfer, L, in a frequency band where the gain of L is less than one. To see why, note that T = L/(I + L). For SISO loops, when |L| << 1, |T| ≈ |L|. Therefore, enforcing the open-loop maximum gain requirement, |L| < 1/|WT|, is roughly equivalent to enforcing |WTT| < 1. For MIMO loops, similar reasoning applies, with ||T|| ≈ σmax(L), where σmax is the largest singular value.
Version History
Introduced in R2014aSee Also
looptune | systune | looptune (for slTuner) (Simulink Control Design) | systune (for slTuner) (Simulink Control Design) | viewGoal | evalGoal | TuningGoal.Gain | TuningGoal.LoopShape | TuningGoal.MinLoopGain | TuningGoal.Margins | slTuner (Simulink Control Design) | sigma