mechss

Sparse second-order state-space model

Since R2020b

Description

Use mechss to represent second-order sparse models using matrices obtained from your finite element analysis (FEA) package. Such sparse models arise from finite element analysis (FEA) and are useful in fields like structural analysis, fluid flow, heat transfer, and electromagnetics. The resultant matrices from this type of modeling are quite large with a sparse pattern. Hence, using mechss is an efficient way to represent such large sparse state-space models in MATLAB^® to perform linear analysis. You can also use mechss to convert a first-order sparss model object or other dynamic system models to a mechss object.

You can use mechss model objects to represent SISO or MIMO state-space models in continuous time or discrete time. In continuous time, a second-order sparse mass-spring-damper model is represented in the following form:

$$\begin{array}{r}\text{M }\ddot{q}(t)+\text{C }\dot{q}(t)+\text{K }q(t)\text{ = B }u(t)\\ y(t)\text{ = F }q(t)+\text{G }\dot{q}(t)+\text{D }u(t)\end{array}$$

Here, the full state vector is given by $$\left[q,\dot{q}\right]$$ where $$q$$ and $$\dot{q}$$ are the displacement and velocity vectors. u and y represent the inputs and outputs, respectively. M, C and K represent the mass, damping and stiffness matrices, respectively. B is the input matrix while F and G are the output matrices for displacement and velocity, respectively. D is the input-to-output matrix.

You can use a mechss object to:

• Perform time-domain and frequency-domain response analysis.

• Specify signal-based connections with other LTI models.

• Specify physical interfaces between components using the interface command.

For more information, see Sparse Model Basics.

Creation

Syntax

sys = mechss(M,C,K,B,F,G,D)

sys = mechss(M,C,K,B,F,G,D,ts)

sys = mechss(M,C,K)

sys = mechss(D)

sys = mechss(___,Name,Value)

sys = mechss(ltiSys)

Description

sys = mechss(M,C,K,B,F,G,D) creates a mechss object representing this continuous-time second-order mass-spring-damper model:

$$\begin{array}{r}\text{M }\ddot{q}(t)+\text{C }\dot{q}(t)+\text{K }q(t)\text{ = B }u(t)\\ y(t)\text{ = F }q(t)+\text{G }\dot{q}(t)+\text{D }u(t)\end{array}$$

Here, M, C, and K represent the mass, damping, and stiffness matrices, respectively. B is the input-to-state matrix while F and G are the displacement-to-output and velocity-to-output matrices resulting from the two components of the state x. D is the input-to-output matrix. You can set M to [] when the mass matrix is an identity matrix. Set G and D to [] or omit them when they are empty.

sys = mechss(M,C,K,B,F,G,D,ts) uses the sample time ts to create a mechss object representing this discrete-time second-order mass-spring-damper model:

$$\begin{array}{r}\text{M }q\left[k+2\right]+\text{C }q\left[k+1\right]+\text{K }q\left[k\right]\text{ = B }u\left[k\right]\\ y\left[k\right]\text{ = F }q\left[k\right]+\text{G }q\left[k+1\right]+\text{D }u\left[k\right]\end{array}$$

To leave the sample time unspecified, set ts to -1.

sys = mechss(M,C,K) creates a mechss model object with the following assumptions:

• Identity matrices for B and F with the same size as mass matrix M

• Matrices of zeros for G and D

sys = mechss(D) creates a mechss model object that represents the static gain D. The output sparse state-space model is equivalent to mechss([],[],[],[],[],[],D).

sys = mechss(___,Name,Value) sets properties of the second-order sparse state-space model using one or more name-value pair arguments. Use this syntax with any of the previous input-argument combinations.

sys = mechss(ltiSys) converts the dynamic system model ltiSys to a second-order sparse state-space model.

Input Arguments

M — Mass matrix

Nq-by-Nq sparse matrix

Mass matrix, specified as an Nq-by-Nq sparse matrix, where Nq is the number of degrees of freedom. This input sets the value of property M.

C — Damping matrix

Nq-by-Nq sparse matrix

Damping matrix, specified as an Nq-by-Nq sparse matrix, where Nq is the number of degrees of freedom. You can also set C=[] to specify zero damping. This input sets the value of property C.

K — Stiffness matrix

Nq-by-Nq sparse matrix

Stiffness matrix, specified as an Nq-by-Nq sparse matrix, where Nq is the number of degrees of freedom. This input sets the value of property K.

B — Input-to-state matrix

Nq-by-Nu sparse matrix

Input-to-state matrix, specified as an Nq-by-Nu sparse matrix, where Nq is the number of degrees of freedom and Nu is the number of inputs. This input sets the value of property B.

F — Displacement-to-output matrix

Ny-by-Nq sparse matrix

Displacement-to-output matrix, specified as an Ny-by-Nq sparse matrix, where Nq is the number of degrees of freedom and Ny is the number of outputs. This input sets the value of property F.

G — Velocity-to-output matrix

Ny-by-Nq sparse matrix

Velocity-to-output matrix, specified as an Ny-by-Nq sparse matrix, where Nq is the number of degrees of freedom and Ny is the number of outputs. This input sets the value of property G.

D — Input-to-output matrix

Ny-by-Nu sparse matrix

Input-to-output matrix, specified as an Ny-by-Nu sparse matrix, where Ny is the number of outputs and Nu is the number of inputs. This input sets the value of property D.

ts — Sample time

scalar

Sample time, specified as a scalar. For more information see the Ts property.

ltiSys — Dynamic system to convert to second-order sparse state-space form

dynamic system model | model array

Dynamic system to convert to second-order sparse state-space form, specified as a SISO or MIMO dynamic system model or array of dynamic system models. Dynamic systems that you can convert include:

• Continuous-time or discrete-time numeric LTI models, such as sparss, tf, zpk, ss, or pid models.

Output Arguments

sys — Output system model

mechss model object

Output system model, returned as a mechss model object.

Properties

M — Mass matrix

Nq-by-Nq sparse matrix

Mass matrix, specified as an Nq-by-Nq sparse matrix where, Nq is the number of degrees of freedom.

C — Damping matrix

Nq-by-Nq sparse matrix

Damping matrix, specified as an Nq-by-Nq sparse matrix where, Nq is the number of degrees of freedom.

K — Stiffness matrix

Nq-by-Nq sparse matrix

Damping matrix, specified as an Nq-by-Nq sparse matrix where, Nq is the number of degrees of freedom.

B — Input-to-state matrix

Nq-by-Nu sparse matrix

Input-to-state matrix, specified as an Nq-by-Nu sparse matrix where, Nq is the number of degrees of freedom and Nu is the number of inputs.

F — Displacement-to-output matrix

Ny-by-Nq sparse matrix

Displacement-to-output matrix, specified as an Ny-by-Nq sparse matrix where, Nq is the number of degrees of freedom and Ny is the number of outputs.

G — Velocity-to-output matrix

Ny-by-Nq sparse matrix

Velocity-to-output matrix, specified as an Ny-by-Nq sparse matrix where, Nq is the number of degrees of freedom and Ny is the number of outputs.

D — Input-to-output matrix

Ny-by-Nu sparse matrix

Input-to-output matrix, specified as an Ny-by-Nu sparse matrix where, Ny is the number of outputs and Nu is the number of inputs. D is also called the static gain matrix, and represents the ratio of the output to the input in steady state condition.

StateInfo — State partition information

structure array

State partition information containing state vector components, interfaces between components and internal signal connecting components, specified as a structure array with the following fields:

• Type — Type includes component, signal or physical interface

• Name — Name of the component, signal or physical interface

• Size — Number of states or degrees of freedom in the partition

You can view the partition information of the sparse state-space model using showStateInfo. You can also sort and order the partitions in your sparse model using xsort.

SolverOptions — Options for model analysis

structure

Options for model analysis, specified as a structure with the following fields:

• UseParallel — Set this option to true to enable parallel computing and false to disable it. Parallel computing is disabled by default. The UseParallel option requires a Parallel Computing Toolbox™ license.

• DAESolver — Use this option to select the type of differential algebraic equation (DAE) solver. The following DAE solvers are available:

  • 'trbdf2' — Fixed-step solver with an accuracy of o(h^2), where h is the step size.[2] This is the default solver for the mechss model object.

  • 'trbdf3' — Fixed-step solver with an accuracy of o(h^3), where h is the step size.

  • 'hht' — Fixed-step solver with an accuracy of o(h^2), where h is the step size.[1]

  Reducing the step size increases accuracy and extends the frequency range where numerical damping is negligible. 'hht' is the fastest but can run into difficulties with high initial acceleration (for example, an impulse response with initial jerk). 'trbdf2' requires about twice as many computations as 'hht' and 'trbdf3' requires another 50% more computations than 'trbdf2'.

  For an example, see Time and Frequency Response of Sparse Second-Order Model.

InternalDelay — Internal delays in the model

vector

Internal delays in the model, specified as a vector. Internal delays arise, for example, when closing feedback loops on systems with delays, or when connecting delayed systems in series or parallel. For more information about internal delays, see Closing Feedback Loops with Time Delays.

For continuous-time models, internal delays are expressed in the time unit specified by the TimeUnit property of the model. For discrete-time models, internal delays are expressed as integer multiples of the sample time Ts. For example, InternalDelay = 3 means a delay of three sampling periods.

You can modify the values of internal delays using the property InternalDelay. However, the number of entries in sys.InternalDelay cannot change, because it is a structural property of the model.

InputDelay — Input delay

0 (default) | scalar | Nu-by-1 vector

Input delay for each input channel, specified as one of the following:

• Scalar — Specify the input delay for a SISO system or the same delay for all inputs of a multi-input system.

• Nu-by-1 vector — Specify separate input delays for input of a multi-input system, where Nu is the number of inputs.

For continuous-time systems, specify input delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify input delays in integer multiples of the sample time, Ts.

For more information, see Time Delays in Linear Systems.

OutputDelay — Output delay

0 (default) | scalar | Ny-by-1 vector

Output delay for each output channel, specified as one of the following:

• Scalar — Specify the output delay for a SISO system or the same delay for all outputs of a multi-output system.

• Ny-by-1 vector — Specify separate output delays for output of a multi-output system, where Ny is the number of outputs.

For continuous-time systems, specify output delays in the time unit specified by the TimeUnit property. For discrete-time systems, specify output delays in integer multiples of the sample time, Ts.

For more information, see Time Delays in Linear Systems.

Ts — Sample time

0 (default) | positive scalar | -1

Sample time, specified as:

• 0 for continuous-time systems.

• A positive scalar representing the sampling period of a discrete-time system. Specify Ts in the time unit specified by the TimeUnit property.

• -1 for a discrete-time system with an unspecified sample time.

Note

Changing Ts does not discretize or resample the model. To convert between continuous-time and discrete-time representations, use c2d and d2c. To change the sample time of a discrete-time system, use d2d.

TimeUnit — Time variable units

'seconds' (default) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

Time variable units, specified as one of the following:

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

Changing TimeUnit has no effect on other properties, but changes the overall system behavior. Use chgTimeUnit to convert between time units without modifying system behavior.

InputName — Input channel names

'' (default) | character vector | cell array of character vectors

Input channel names, specified as one of the following:

• A character vector, for single-input models.

• A cell array of character vectors, for multi-input models.

• '', no names specified, for any input channels.

Alternatively, you can assign input names for multi-input models using automatic vector expansion. For example, if sys is a two-input model, enter the following.

sys.InputName = 'controls';

The input names automatically expand to {'controls(1)';'controls(2)'}.

You can use the shorthand notation u to refer to the InputName property. For example, sys.u is equivalent to sys.InputName.

Use InputName to:

• Identify channels on model display and plots.

• Extract subsystems of MIMO systems.

• Specify connection points when interconnecting models.

InputUnit — Input channel units

'' (default) | character vector | cell array of character vectors

Input channel units, specified as one of the following:

• A character vector, for single-input models.

• A cell array of character vectors, for multi-input models.

• '', no units specified, for any input channels.

Use InputUnit to specify input signal units. InputUnit has no effect on system behavior.

InputGroup — Input channel groups

structure

Input channel groups, specified as a structure. Use InputGroup to assign the input channels of MIMO systems into groups and refer to each group by name. The field names of InputGroup are the group names and the field values are the input channels of each group. For example, enter the following to create input groups named controls and noise that include input channels 1 and 2, and 3 and 5, respectively.

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

You can then extract the subsystem from the controls inputs to all outputs using the following.

sys(:,'controls')

By default, InputGroup is a structure with no fields.

OutputName — Output channel names

'' (default) | character vector | cell array of character vectors

Output channel names, specified as one of the following:

• A character vector, for single-output models.

• A cell array of character vectors, for multi-output models.

• '', no names specified, for any output channels.

Alternatively, you can assign output names for multi-output models using automatic vector expansion. For example, if sys is a two-output model, enter the following.

sys.OutputName = 'measurements';

The output names automatically expand to {'measurements(1)';'measurements(2)'}.

You can also use the shorthand notation y to refer to the OutputName property. For example, sys.y is equivalent to sys.OutputName.

Use OutputName to:

• Identify channels on model display and plots.

• Extract subsystems of MIMO systems.

• Specify connection points when interconnecting models.

OutputUnit — Output channel units

'' (default) | character vector | cell array of character vectors

Output channel units, specified as one of the following:

• A character vector, for single-output models.

• A cell array of character vectors, for multi-output models.

• '', no units specified, for any output channels.

Use OutputUnit to specify output signal units. OutputUnit has no effect on system behavior.

OutputGroup — Output channel groups

structure

Output channel groups, specified as a structure. Use OutputGroup to assign the output channels of MIMO systems into groups and refer to each group by name. The field names of OutputGroup are the group names and the field values are the output channels of each group. For example, create output groups named temperature and measurement that include output channels 1, and 3 and 5, respectively.

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

You can then extract the subsystem from all inputs to the measurement outputs using the following.

sys('measurement',:)

By default, OutputGroup is a structure with no fields.

Notes — User-specified text

{} (default) | character vector | cell array of character vectors

User-specified text that you want to associate with the system, specified as a character vector or cell array of character vectors. For example, 'System is MIMO'.

UserData — User-specified data

[] (default) | any MATLAB data type

User-specified data that you want to associate with the system, specified as any MATLAB data type.

Name — System name

'' (default) | character vector

System name, specified as a character vector. For example, 'system_1'.

SamplingGrid — Sampling grid for model arrays

structure array

Sampling grid for model arrays, specified as a structure array.

Use SamplingGrid to track the variable values associated with each model in a model array.

Set the field names of the structure to the names of the sampling variables. Set the field values to the sampled variable values associated with each model in the array. All sampling variables must be numeric scalars, and all arrays of sampled values must match the dimensions of the model array.

For example, you can create an 11-by-1 array of linear models, sysarr, by taking snapshots of a linear time-varying system at times t = 0:10. The following code stores the time samples with the linear models.

 sysarr.SamplingGrid = struct('time',0:10)

Similarly, you can create a 6-by-9 model array, M, by independently sampling two variables, zeta and w. The following code maps the (zeta,w) values to M.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

By default, SamplingGrid is a structure with no fields.

Object Functions

The following lists show functions you can use with mechss model objects.

Modeling

sparss	Sparse first-order state-space model
getx0	Map initial conditions from a mechss object to a sparss object
full	Convert sparse models to dense storage
imp2exp	Convert implicit linear relationship to explicit input-output relation
inv	Invert dynamic system models
getDelayModel	State-space representation of internal delays

Data Access

sparssdata	Access first-order sparse state-space model data
mechssdata	Access second-order sparse state-space model data
showStateInfo	State vector map for sparse model
spy	Visualize sparsity pattern of a sparse model

Time and Frequency Response

step	Step response of dynamic system
impulse	Impulse response plot of dynamic system; impulse response data
initial	System response to initial states of state-space model
lsim	Compute time response simulation data of dynamic system to arbitrary inputs
bode	Bode frequency response of dynamic system
nyquist	Nyquist response of dynamic system
nichols	Nichols response of dynamic system
sigma	Singular values of frequency response of dynamic system
passiveplot	Compute or plot passivity index as function of frequency
dcgain	Low-frequency (DC) gain of LTI system
evalfr	Evaluate system response at specific frequency
freqresp	Evaluate system response over a grid of frequencies

Model Interconnection

interface	Specify physical connections between components of mechss model
xsort	Sort states based on state partition
feedback	Feedback connection of multiple models
parallel	Parallel connection of two models
append	Group models by appending their inputs and outputs
connect	Block diagram interconnections of dynamic systems
lft	Generalized feedback interconnection of two models (Redheffer star product)
series	Series connection of two models

Examples

Continuous-Time Sparse Second-Order Model

For this example, consider the sparse matrices for the 3-D beam model subjected to an impulsive point load at its tip in the file sparseBeam.mat.

Extract the sparse matrices from sparseBeam.mat.

load('sparseBeam.mat','M','K','B','F','G','D');

Create the mechss model object by specifying [] for matrix C, since there is no damping.

sys = mechss(M,[],K,B,F,G,D)

Sparse continuous-time second-order model with 3 outputs, 1 inputs, and 3408 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

The output sys is a mechss model object containing a 3-by-1 array of sparse models with 3408 degrees of freedom, 1 input, and 3 outputs.

You can use the spy command to visualize the sparsity of the mechss model object.

spy(sys)

Discrete-Time Sparse Second-Order Model

For this example, consider the sparse matrices of the discrete system in the file discreteSOSparse.mat.

Load the sparse matrices from discreteSOSparse.mat.

load('discreteSOSparse.mat','M','C','K','B','F','G','D','ts');

Create the discrete-time mechss model object by specifying the sample time ts.

sys = mechss(M,C,K,B,F,G,D,ts)

Sparse discrete-time second-order model with 1 outputs, 1 inputs, and 28408 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

The output sys is a discrete-time mechss model object with 28408 degrees of freedom, 1 input, and 1 output.

You can use the spy command to visualize the sparsity pattern of the mechss model object. You can right-click on the plot to select matrices to be displayed.

spy(sys)

Array of Sparse Second-Order Models

For this example, consider sparseSOArray.mat which contains three sets of sparse matrices that define multiple sparse second-order state-space models.

Extract the data from sparseSOArray.mat.

load('sparseSOArray.mat');

Preallocate a 3-by-1 array of mechss models.

sys = mechss(zeros(1,1,3));

Next, use indexed assignment to populate the 3-by-1 array with sparse second-order models.

sys(:,:,1) = mechss(M1,[],K1,B1,F1,G1,[]);
sys(:,:,2) = mechss(M2,[],K2,B2,F2,G2,[]);
sys(:,:,3) = mechss(M3,[],K3,B3,F3,G3,[]);
size(sys)

3x1 array of sparse second-order models.
Each model has 1 outputs, 1 inputs, and between 385 and 738 degrees of freedom.

Alternatively, you can also create an array of sparse second-order models using the stack command when you have models with the same I/O sizes.

Copyright 2020 The MathWorks, Inc

MIMO Static Gain Sparse Second-Order Model

Create a static gain MIMO sparse second-order state-space model.

Consider the following two-input, three-output static gain matrix:

$$D=\left[\begin{array}{cc}1& 5\\ 2& 3\\ 5& 9\end{array}\right]$$

Specify the gain matrix and create the static gain sparse second-order state-space model.

D = [1,5;2,3;5,9];
sys = mechss(D);
size(sys)

Sparse second-order model with 3 outputs, 2 inputs, and 0 degrees of freedom.

Mass-Spring-Damper Sparse Second-Order Model

For this example, consider sparseSOSignal.mat which contains the mass, stiffness, and damping sparse matrices.

Load the sparse matrices from sparseSOSignal.mat and create the sparse second-order model object.

load('sparseSOModel.mat','M','C','K');
sys = mechss(M,C,K);

mechss creates the model object sys with the following assumptions:

• Identity matrices for B and F with the same size as mass matrix M.

• Zero matrices for G and D.

Convert First-Order Sparse Model to Second-Order Sparse Model Representation

For this example, consider sparssModel.mat that contains a sparss model object ltiSys.

Load the sparss model object from sparssModel.mat.

load('sparssModel.mat','ltiSys');
ltiSys

Sparse continuous-time state-space model with 1 outputs, 1 inputs, and 354 states.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help sparssOptions" for available solver options for this model.

Use the mechss command to convert to mechss model object representation.

sys = mechss(ltiSys)

Sparse continuous-time second-order model with 1 outputs, 1 inputs, and 354 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

Time and Frequency Response of Sparse Second-Order Model

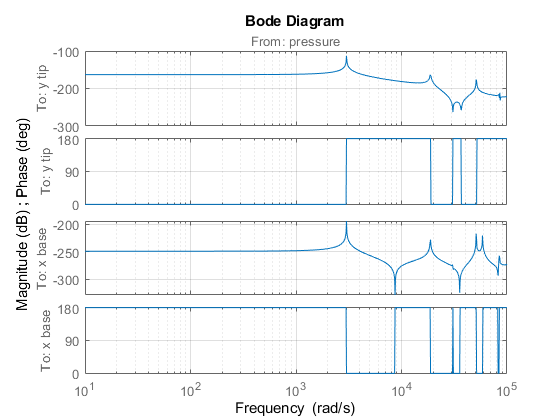
For this example, consider tuningForkData.mat that contains the sparse second-order model of a tuning fork being struck gently but quickly on one of its tines. The system has one input, the pressure applied on one of its tines, which results in two outputs - the displacements at the tip and base of the tuning fork.

Load the sparse matrices from tuningForkData.mat into the workspace and create the mechss model object.

load('tuningForkData.mat','M','K','B','F');
sys = mechss(M,[],K,B,F,'InputName','pressure','Outputname',{'y tip','x base'})

Next, set solver options for the model by setting the UseParallel parameter to true and the DAESolver to use trbdf3. Use spy to inspect the model structure. Enabling parallel computing requires a Parallel Computing Toolbox™ license.

sys.SolverOptions.UseParallel = true;
sys.SolverOptions.DAESolver = 'trbdf3';
spy(sys)

You can also use showStateInfo to examine the components.

showStateInfo(sys)

Use step to obtain the step response plot of the system. You need to provide the time vector or final time for sparse models.

t = linspace(0,0.5,1000);
step(sys,t)

Next, obtain the Bode plot to examine the frequency response. You need to provide the frequency vector for sparse models.

w = logspace(1,5,1000);
bode(sys,w), grid

Sparse Second-Order Model in a Feedback Loop

For this example, consider sparseSOSignal.mat that contains a sparse second-order model. Define an actuator, sensor, and controller and connect them together with the plant in a feedback loop.

Load the sparse matrices and create the mechss object.

load sparseSOSignal.mat
plant = mechss(M,C,K,B,F,[],[],'Name','Plant');

Next, create an actuator and sensor using transfer functions.

act = tf(1,[1 0.5 3],'Name','Actuator');
sen = tf(1,[0.02 7],'Name','Sensor');

Create a PID controller object for the plant.

con = pid(1,1,0.1,0.01,'Name','Controller');

Use the feedback command to connect the plant, sensor, actuator, and controller in a feedback loop.

sys = feedback(sen*plant*act*con,1)

Sparse continuous-time second-order model with 1 outputs, 1 inputs, and 7111 degrees of freedom.

Use "spy" and "showStateInfo" to inspect model structure. 
Type "help mechssOptions" for available solver options for this model.

The resultant system sys is a mechss object since mechss objects take precedence over all other model object types.

Use showStateInfo to view the component and signal groups.

showStateInfo(sys)

The state groups are:

    Type          Name       Size
  -------------------------------
  Component      Sensor         1
  Component      Plant       7102
  Signal                        1
  Component     Actuator        2
  Signal                        1
  Component    Controller       2
  Signal                        1
  Signal                        1

Use xsort to sort the components and signals, and then view the component and signal groups.

sysSort = xsort(sys);
showStateInfo(sysSort)

The state groups are:

    Type          Name       Size
  -------------------------------
  Component      Sensor         1
  Component      Plant       7102
  Component     Actuator        2
  Component    Controller       2
  Signal                        4

Observe that the components are now ordered before the signal partition. The signals are now sorted and grouped together in a single partition.

You can also visualize the sparsity pattern of the resultant system using spy.

spy(sysSort)

Physical Connections Between Components in Sparse Second-Order Model

For this example, consider a structural model that consists of two square plates connected with pillars at each vertex as depicted in the figure below. The lower plate is attached rigidly to the ground while the pillars are attached rigidly to each vertex of the square plate.

Load the finite element model matrices contained in platePillarModel.mat and create the sparse second-order model representing the above system.

load('platePillarModel.mat')
model = ...
   mechss(M1,[],K1,B1,F1,'Name','Plate1') + ...
   mechss(M2,[],K2,B2,F2,'Name','Plate2') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar3') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar4') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar5') + ...
   mechss(Mp,[],Kp,Bp,Fp,'Name','Pillar6');
sys = model;

Use showStateInfo to examine the components of the mechss model object.

showStateInfo(sys)

The state groups are:

    Type        Name      Size
  ----------------------------
  Component    Plate1     2646
  Component    Plate2     2646
  Component    Pillar3     132
  Component    Pillar4     132
  Component    Pillar5     132
  Component    Pillar6     132

Now, load the interfaced degree of freedom (DOF) index data from dofData.mat and use interface to create the physical connections between the two plates and the four pillars. dofs is a 6x7 cell array where the first two rows contain DOF index data for the first and second plates while the remaining four rows contain index data for the four pillars. By default, the function uses dual-assembly method of physical coupling.

load('dofData.mat','dofs')
for i=3:6
   sys = interface(sys,"Plate1",dofs{1,i},"Pillar"+i,dofs{i,1});
   sys = interface(sys,"Plate2",dofs{2,i},"Pillar"+i,dofs{i,2});
end

Specify connection between the bottom plate and the ground.

sysConDual = interface(sys,"Plate2",dofs{2,7});

Use showStateInfo to confirm the physical interfaces.

showStateInfo(sysConDual)

The state groups are:

    Type            Name         Size
  -----------------------------------
  Component        Plate1        2646
  Component        Plate2        2646
  Component       Pillar3         132
  Component       Pillar4         132
  Component       Pillar5         132
  Component       Pillar6         132
  Interface    Plate1-Pillar3      12
  Interface    Plate2-Pillar3      12
  Interface    Plate1-Pillar4      12
  Interface    Plate2-Pillar4      12
  Interface    Plate1-Pillar5      12
  Interface    Plate2-Pillar5      12
  Interface    Plate1-Pillar6      12
  Interface    Plate2-Pillar6      12
  Interface    Plate2-Ground        6

You can use spy to visualize the sparse matrices in the final model.

spy(sysConDual)

Now, specify physical connections using the primal-assembly method.

sys = model;
for i=3:6
   sys = interface(sys,"Plate1",dofs{1,i},"Pillar"+i,dofs{i,1},'primal');
   sys = interface(sys,"Plate2",dofs{2,i},"Pillar"+i,dofs{i,2},'primal');
end
sysConPrimal = interface(sys,"Plate2",dofs{2,7},'primal');

Use showStateInfo to confirm the physical interfaces.

showStateInfo(sysConPrimal)

The state groups are:

    Type        Name      Size
  ----------------------------
  Component    Plate1     2646
  Component    Plate2     2640
  Component    Pillar3     108
  Component    Pillar4     108
  Component    Pillar5     108
  Component    Pillar6     108

Primal assembly eliminates half of the redundant DOFs associated with the shared set of DOFs in the global finite element mesh.

You can use spy to visualize the sparse matrices in the final model.

spy(sysConPrimal)

The data set for this example was provided by Victor Dolk from ASML.

References

[1] H. Hilber, T. Hughes & R. Taylor. " Improved numerical dissipation for time integration algorithms in structural dynamics." Earthquake Engineering and Structural Dynamics, vol. 5, no. 3, pp. 283-292, 1977.

[2] M. Hosea and L. Shampine. "Analysis and implementation of TR-BDF2." Applied Numerical Mathematics, vol. 20, no. 1-2, pp. 21-37, 1996.

Version History

Introduced in R2020b