qorthwavf
Kingsbury Q-shift filters
Description
[
returns the Kingsbury Q-shift filters for the Q-shift complex dual-tree transform. The
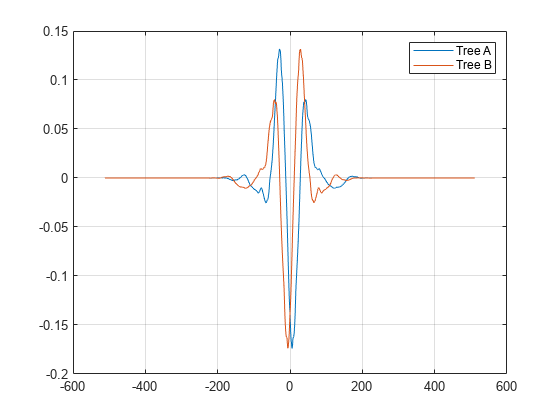
integer LoDa,LoDb,HiDa,HiDb,LoRa,LoRb,HiRa,HiRb] = qorthwavf(num)num refers to the number of nonzero coefficients (taps) in the
filter. Valid options for num are 6, 10, 14, 16, and 18. All filters
are of even lengths and the tree B filters are the time reverse of the tree A
filters.
Examples
Input Arguments
Output Arguments
References
[1] Antonini, M., M. Barlaud, P. Mathieu, and I. Daubechies. “Image Coding Using Wavelet Transform.” IEEE Transactions on Image Processing 1, no. 2 (April 1992): 205–20. https://doi.org/10.1109/83.136597.
[2] Kingsbury, Nick. “Complex Wavelets for Shift Invariant Analysis and Filtering of Signals.” Applied and Computational Harmonic Analysis 10, no. 3 (May 2001): 234–53. https://doi.org/10.1006/acha.2000.0343.
[3] Le Gall, D., and A. Tabatabai. “Sub-Band Coding of Digital Images Using Symmetric Short Kernel Filters and Arithmetic Coding Techniques.” In ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing, 761–64. New York, NY, USA: IEEE, 1988. https://doi.org/10.1109/ICASSP.1988.196696.
Extended Capabilities
Version History
Introduced in R2020a