incrementalRegressionLinear

Linear regression model for incremental learning

Since R2020b

Description

incrementalRegressionLinear creates an incrementalRegressionLinear model object, which represents an incremental linear model for regression problems. Supported learners include support vector machine (SVM) and least squares.

Unlike other Statistics and Machine Learning Toolbox™ model objects, incrementalRegressionLinear can be called directly. Also, you can specify learning options, such as performance metrics configurations, parameter values, and the objective solver, before fitting the model to data. After you create an incrementalRegressionLinear object, it is prepared for incremental learning.

incrementalRegressionLinear is best suited for incremental learning. For a traditional approach to training an SVM or linear regression model (such as creating a model by fitting it to data, performing cross-validation, tuning hyperparameters, and so on), see fitrsvm or fitrlinear.

Creation

You can create an incrementalRegressionLinear model object in several ways:

• Call the function directly — Configure incremental learning options, or specify initial values for linear model parameters and hyperparameters, by calling incrementalRegressionLinear directly. This approach is best when you do not have data yet or you want to start incremental learning immediately.

• Convert a traditionally trained model — To initialize an linear regression model for incremental learning using the model coefficients and hyperparameters of a trained model object, you can convert the traditionally trained model to an incrementalRegressionLinear model object by passing it to the incrementalLearner function. This table contains links to the appropriate reference pages.

  Convertible Model Object	Conversion Function
  RegressionSVM or CompactRegressionSVM	incrementalLearner
  RegressionLinear	incrementalLearner

• Call an incremental learning function — fit, updateMetrics, and updateMetricsAndFit accept a configured incrementalRegressionLinear model object and data as input, and return an incrementalRegressionLinear model object updated with information learned from the input model and data.

Syntax

Mdl = incrementalRegressionLinear()

Mdl = incrementalRegressionLinear(Name,Value)

Description

Mdl = incrementalRegressionLinear() returns a default incremental model object for linear regression, Mdl. Properties of a default model contain placeholders for unknown model parameters. You must train a default model before you can track its performance or generate predictions from it.

Mdl = incrementalRegressionLinear(Name,Value) sets properties and additional options using name-value arguments. Enclose each name in quotes. For example, incrementalRegressionLinear('Beta',[0.1 0.3],'Bias',1,'MetricsWarmupPeriod',100) sets the vector of linear model coefficients β to [0.1 0.3], the bias β₀ to 1, and the metrics warm-up period to 100.

Input Arguments

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Standardize',true standardizes the predictor data using the predictor means and standard deviations estimated during the estimation period.

Metrics — Model performance metrics to track during incremental learning

"epsiloninsensitive" | "mse" | string vector | function handle | cell vector | structure array

Model performance metrics to track during incremental learning, specified as a built-in loss function name, string vector of names, function handle (@metricName), structure array of function handles, or cell vector of names, function handles, or structure arrays.

When Mdl is warm (see IsWarm), updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of Mdl.

The following table lists the built-in loss function names and which learners, specified in Learner, support them. You can specify more than one loss function by using a string vector.

Name	Description	Learner Supporting Metric
"epsiloninsensitive"	Epsilon insensitive loss	'svm'
"mse"	Weighted mean squared error	'svm' and 'leastsquares'

For more details on the built-in loss functions, see loss.

Example: 'Metrics',["epsiloninsensitive" "mse"]

To specify a custom function that returns a performance metric, use function handle notation. The function must have this form:

metric = customMetric(Y,YFit)

• The output argument metric is an n-by-1 numeric vector, where each element is the loss of the corresponding observation in the data processed by the incremental learning functions during a learning cycle.

• You specify the function name (customMetric).

• Y is a length n numeric vector of observed responses, where n is the sample size.

• YFit is a length n numeric vector of corresponding predicted responses.

To specify multiple custom metrics and assign a custom name to each, use a structure array. To specify a combination of built-in and custom metrics, use a cell vector.

Example: 'Metrics',struct('Metric1',@customMetric1,'Metric2',@customMetric2)

Example: 'Metrics',{@customMetric1 @customMetric2 'mse' struct('Metric3',@customMetric3)}

updateMetrics and updateMetricsAndFit store specified metrics in a table in the property Metrics. The data type of Metrics determines the row names of the table.

'Metrics' Value Data Type	Description of Metrics Property Row Name	Example
String or character vector	Name of corresponding built-in metric	Row name for "epsiloninsensitive" is "EpsilonInsensitiveLoss"
Structure array	Field name	Row name for struct('Metric1',@customMetric1) is "Metric1"
Function handle to function stored in a program file	Name of function	Row name for @customMetric is "customMetric"
Anonymous function	CustomMetric_j, where j is metric j in Metrics	Row name for @(Y,YFit)customMetric(Y,YFit)... is CustomMetric_1

By default:

• Metrics is "epsiloninsensitive" if Learner is 'svm'.

• Metrics is "mse" if Learner is 'leastsquares'.

For more details on performance metrics options, see Performance Metrics.

Data Types: char | string | struct | cell | function_handle

Standardize — Flag to standardize predictor data

'auto' (default) | false | true

Flag to standardize the predictor data, specified as a value in this table.

Value	Description
'auto'	incrementalRegressionLinear determines whether the predictor variables need to be standardized. See Standardize Data.
true	The software standardizes the predictor data. For more details, see Standardize Data.
false	The software does not standardize the predictor data.

Example: 'Standardize',true

Data Types: logical | char | string

Shuffle — Flag for shuffling observations

true (default) | false

Flag for shuffling the observations at each iteration, specified as a value in this table.

Value	Description
true	The software shuffles the observations in an incoming chunk of data before the fit function fits the model. This action reduces bias induced by the sampling scheme.
false	The software processes the data in the order received.

This option is valid only when Solver is 'scale-invariant'. When Solver is 'sgd' or 'asgd', the software always shuffles the observations in an incoming chunk of data before processing the data.

Example: 'Shuffle',false

Data Types: logical

Properties

You can set most properties by using name-value argument syntax only when you call incrementalRegressionLinear. You can set some properties when you call incrementalLearner to convert a traditionally trained model. You cannot set the properties FittedLoss, NumTrainingObservations, Mu, Sigma, SolverOptions, and IsWarm.

Regression Model Parameters

Beta — Linear model coefficients β

numeric vector

This property is read-only.

Linear model coefficients β, specified as a NumPredictors-by-1 numeric vector.

Incremental fitting functions estimate Beta during training. The default initial Beta value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the initial value is specified by the corresponding property of the traditionally trained model.

• Otherwise, the initial value is zeros(NumPredictors,1).

Data Types: single | double

Bias — Model intercept β₀

numeric scalar

This property is read-only.

Model intercept β₀, or bias term, specified as a numeric scalar.

Incremental fitting functions estimate Bias during training. The default initial Bias value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the initial value is specified by the corresponding property of the traditionally trained model.

• Otherwise, the initial value is 0.

Data Types: single | double

Epsilon — Half of the width of epsilon insensitive band

'auto' | nonnegative scalar

This property is read-only.

Half of the width of the epsilon insensitive band, specified as 'auto' or a nonnegative scalar. incrementalRegressionLinear stores the Epsilon value as a numeric scalar.

If you specify 'auto' when you call incrementalRegressionLinear, incremental fitting functions estimate Epsilon during the estimation period, specified by EstimationPeriod, using this procedure:

• If iqr(Y) ≠ 0, Epsilon is iqr(Y)/13.49, where Y is the estimation period response data.

• If iqr(Y) = 0 or before you fit Mdl to data, Epsilon is 0.1.

The default Epsilon value depends on how you create the model:

• If you convert a traditionally trained SVM regression model (Learner is 'svm'), Epsilon is specified by the corresponding property of the traditionally trained model.

• Otherwise, the default value is 'auto'.

If Learner is 'leastsquares', you cannot set Epsilon and its value is NaN.

Data Types: single | double

FittedLoss — Loss function used to fit linear model

'epsiloninsensitive' | 'mse'

This property is read-only.

Loss function used to fit the linear model, specified as 'epsiloninsensitive' or 'mse'.

Value	Algorithm	Loss Function	Learner Value
'epsiloninsensitive'	Support vector machine regression	Epsilon insensitive: $$\ell \left[y,f\left(x\right)\right]=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right]$$	'svm'
'mse'	Linear regression through ordinary least squares	Mean squared error (MSE): $$\ell \left[y,f\left(x\right)\right]=\frac{1}{2}{\left[y-f\left(x\right)\right]}^2$$	'leastsquares'

Learner — Linear regression model type

'svm' | 'leastsquares'

This property is read-only.

Linear regression model type, specified as 'svm' or 'leastsquares'. incrementalRegressionLinear stores the Learner value as a character vector.

In the following table, $$f\left(x\right)=x\beta +b.$$

• β is Beta.

• x is an observation from p predictor variables.

• β₀ is Bias.

Value	Algorithm	Loss Function	FittedLoss Value
'svm'	Support vector machine regression	Epsilon insensitive: $$\ell \left[y,f\left(x\right)\right]=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right]$$	'epsiloninsensitive'
'leastsquares'	Linear regression through ordinary least squares	Mean squared error (MSE): $$\ell \left[y,f\left(x\right)\right]=\frac{1}{2}{\left[y-f\left(x\right)\right]}^2$$	'mse'

The default Learner value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl:

  • Learner is 'svm' when the traditionally trained model is RegressionSVM or CompactRegressionSVM.

  • Learner is specified by the corresponding property of the traditionally trained model when the traditionally trained model is RegressionLinear.

• Otherwise, the default value is 'svm'.

Data Types: char | string

NumPredictors — Number of predictor variables

nonnegative numeric scalar

This property is read-only.

Number of predictor variables, specified as a nonnegative numeric scalar.

The default NumPredictors value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, NumPredictors is specified by the corresponding property of the traditionally trained model.

• If you create Mdl by calling incrementalRegressionLinear directly, you can specify NumPredictors by using name-value argument syntax. If you do not specify the value, then the default value is 0, and incremental fitting functions infer NumPredictors from the predictor data during training.

Data Types: double

NumTrainingObservations — Number of observations fit to incremental model

0 (default) | nonnegative numeric scalar

This property is read-only.

Number of observations fit to the incremental model Mdl, specified as a nonnegative numeric scalar. NumTrainingObservations increases when you pass Mdl and training data to fit or updateMetricsAndFit.

Note

If you convert a traditionally trained model to create Mdl, incrementalRegressionLinear does not add the number of observations fit to the traditionally trained model to NumTrainingObservations.

Data Types: double

ResponseTransform — Response transformation function

'none' | function handle

This property is read-only.

Response transformation function, specified as 'none' or a function handle. incrementalRegressionLinear stores the ResponseTransform value as a character vector or function handle.

ResponseTransform describes how incremental learning functions transform raw response values.

For a MATLAB^® function or a function that you define, enter its function handle; for example, 'ResponseTransform',@function, where function accepts an n-by-1 vector (the original responses) and returns a vector of the same length (the transformed responses).

The default ResponseTransform value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, ResponseTransform is specified by the corresponding property of the traditionally trained model.

• Otherwise, the default value is "none".

Data Types: char | string | function_handle

Training Parameters

EstimationPeriod — Number of observations processed to estimate hyperparameters

nonnegative integer

This property is read-only.

Number of observations processed by the incremental model to estimate hyperparameters before training or tracking performance metrics, specified as a nonnegative integer.

Note

• If Mdl is prepared for incremental learning (all hyperparameters required for training are specified), incrementalRegressionLinear forces EstimationPeriod to 0.

• If Mdl is not prepared for incremental learning, incrementalRegressionLinear sets EstimationPeriod to 1000.

For more details, see Estimation Period.

Data Types: single | double

FitBias — Linear model intercept inclusion flag

true | false

This property is read-only.

Linear model intercept inclusion flag, specified as true or false.

Value	Description
true	incrementalRegressionLinear includes the bias term β0 in the linear model, which incremental fitting functions fit to data.
false	incrementalRegressionLinear sets β0 = 0.

If Bias ≠ 0, FitBias must be true. In other words, incrementalRegressionLinear does not support an equality constraint on β₀.

The default FitBias value depends on how you create the model:

• If you convert a traditionally trained linear regression model (RegressionLinear) to create Mdl, FitBias is specified by the FitBias value of the ModelParameters property of the traditionally trained model.

• Otherwise, the default value is true.

Data Types: logical

Mu — Predictor means

vector of numeric values | []

This property is read-only.

Predictor means, specified as a numeric vector.

If Mu is an empty array [] and you specify 'Standardize',true, incremental fitting functions set Mu to the predictor variable means estimated during the estimation period specified by EstimationPeriod.

You cannot specify Mu directly.

Data Types: single | double

Sigma — Predictor standard deviations

vector of numeric values | []

This property is read-only.

Predictor standard deviations, specified as a numeric vector.

If Sigma is an empty array [] and you specify 'Standardize',true, incremental fitting functions set Sigma to the predictor variable standard deviations estimated during the estimation period specified by EstimationPeriod.

You cannot specify Sigma directly.

Data Types: single | double

Solver — Objective function minimization technique

'scale-invariant' | 'sgd' | 'asgd'

This property is read-only.

Objective function minimization technique, specified as 'scale-invariant', 'sgd', or 'asgd'. incrementalRegressionLinear stores the Solver value as a character vector.

Value	Description	Notes
'scale-invariant'	Adaptive scale-invariant solver for incremental learning [1]	This algorithm is parameter free and can adapt to differences in predictor scales. Try this algorithm before using SGD or ASGD. To shuffle an incoming chunk of data before the fit function fits the model, set Shuffle to true.
'sgd'	Stochastic gradient descent (SGD) [3][2]	To train effectively with SGD, standardize the data and specify adequate values for hyperparameters using options listed in SGD and ASGD Solver Parameters. The fit function always shuffles an incoming chunk of data before fitting the model.
'asgd'	Average stochastic gradient descent (ASGD) [4]	To train effectively with ASGD, standardize the data and specify adequate values for hyperparameters using options listed in SGD and ASGD Solver Parameters. The fit function always shuffles an incoming chunk of data before fitting the model.

The default Solver value depends on how you create the model:

• If you create Mdl by calling incrementalRegressionLinear directly, the default value is 'scale-invariant'.

• If you convert a traditionally trained linear regression model (RegressionLinear) to create Mdl, and the traditionally trained model's Regularization property is 'ridge (L2)' and ModelParameters.Solver is 'sgd' or 'asgd', Solver is specified by the Solver value of the ModelParameters property of the traditionally trained model.

• Otherwise, the Solver name-value argument of the incrementalLearner function sets this property. The default value of the argument is 'scale-invariant'.

Data Types: char | string

SolverOptions — Objective solver configurations

structure array

This property is read-only.

Objective solver configurations, specified as a structure array. The fields of SolverOptions are properties specific to the specified solver Solver.

Data Types: struct

SGD and ASGD Solver Parameters

BatchSize — Mini-batch size

positive integer

This property is read-only.

Mini-batch size, specified as a positive integer. At each learning cycle during training, incrementalRegressionLinear uses BatchSize observations to compute the subgradient.

The number of observations for the last mini-batch (last learning cycle in each function call of fit or updateMetricsAndFit) can be smaller than BatchSize. For example, if you supply 25 observations to fit or updateMetricsAndFit, the function uses 10 observations for the first two learning cycles and 5 observations for the last learning cycle.

The default BatchSize value depends on how you create the model:

• If you create Mdl by calling incrementalRegressionLinear directly, the default value is 10.

• If you convert a traditionally trained linear regression model (RegressionLinear) to create Mdl, and the traditionally trained model's Regularization property is 'ridge (L2)' and ModelParameters.Solver is 'sgd' or 'asgd', BatchSize is specified by the BatchSize value of the ModelParameters property of the traditionally trained model.

• Otherwise, the BatchSize name-value argument of the incrementalLearner function sets this property. The default value of the argument is 10.

Data Types: single | double

Lambda — Ridge (L2) regularization term strength

nonnegative scalar

This property is read-only.

Ridge (L2) regularization term strength, specified as a nonnegative scalar.

The default Lambda value depends on how you create the model:

• If you create Mdl by calling incrementalRegressionLinear directly, the default value is 1e-5.

• If you convert a traditionally trained linear regression model (RegressionLinear) to create Mdl, and the traditionally trained model's Regularization property is 'ridge (L2)' and ModelParameters.Solver is 'sgd' or 'asgd', Lambda is specified by the corresponding property of the traditionally trained model.

• Otherwise, the Lambda name-value argument of the incrementalLearner function sets this property. The default value of the argument is 1e-5.

Data Types: double | single

LearnRate — Initial learning rate

'auto' | positive scalar

This property is read-only.

Initial learning rate, specified as 'auto' or a positive scalar. incrementalRegressionLinear stores the LearnRate value as a positive scalar.

The learning rate controls the optimization step size by scaling the objective subgradient. LearnRate specifies an initial value for the learning rate, and LearnRateSchedule determines the learning rate for subsequent learning cycles.

When you specify 'auto':

• The initial learning rate is 0.7.

• If EstimationPeriod > 0, fit and updateMetricsAndFit change the rate to 1/sqrt(1+max(sum(X.^2,obsDim))) at the end of EstimationPeriod. When the observations are the columns of the predictor data X collected during the estimation period, the obsDim value is 1; otherwise, the value is 2.

The default LearnRate value depends on how you create the model:

• If you create Mdl by calling incrementalRegressionLinear directly, the default value is 'auto'.

• If you convert a traditionally trained linear regression model (RegressionLinear) to create Mdl, and the traditionally trained model's Regularization property is 'ridge (L2)' and ModelParameters.Solver is 'sgd' or 'asgd', LearnRate is specified by the LearnRate value of the ModelParameters property of the traditionally trained model.

• Otherwise, the LearnRate name-value argument of the incrementalLearner function sets this property. The default value of the argument is 'auto'.

Example: 'LearnRate',0.001

Data Types: single | double | char | string

LearnRateSchedule — Learning rate schedule

'decaying' | 'constant'

This property is read-only.

Learning rate schedule, specified as a value in this table, where LearnRate specifies the initial learning rate ɣ₀. incrementalRegressionLinear stores the LearnRateSchedule value as a character vector.

Value	Description
'constant'	The learning rate is ɣ0 for all learning cycles.
'decaying'	The learning rate at learning cycle t is $${\gamma }_t=\frac{{\gamma }_0}{{\left(1+\lambda {\gamma }_{0}t\right)}^c}.$$ λ is the value of Lambda. If Solver is 'sgd', c = 1. If Solver is 'asgd': c = 2/3 if Learner is 'leastsquares'. c = 3/4 if Learner is 'svm' [4].

The default LearnRateSchedule value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the LearnRateSchedule name-value argument of the incrementalLearner function sets this property. The default value of the argument is 'decaying'.

• Otherwise, the default value is 'decaying'.

Data Types: char | string

Performance Metrics Parameters

IsWarm — Flag indicating whether model tracks performance metrics

false or 0 | true or 1

This property is read-only.

Flag indicating whether the incremental model tracks performance metrics, specified as logical 0 (false) or 1 (true).

The incremental model Mdl is warm (IsWarm becomes true) after incremental fitting functions fit (EstimationPeriod + MetricsWarmupPeriod) observations to the incremental model.

Value	Description
true or 1	The incremental model Mdl is warm. Consequently, updateMetrics and updateMetricsAndFit track performance metrics in the Metrics property of Mdl.
false or 0	updateMetrics and updateMetricsAndFit do not track performance metrics.

Data Types: logical

Metrics — Model performance metrics

table

This property is read-only.

Model performance metrics updated during incremental learning by updateMetrics and updateMetricsAndFit, specified as a table with two columns and m rows, where m is the number of metrics specified by the Metrics name-value argument.

The columns of Metrics are labeled Cumulative and Window.

• Cumulative: Element j is the model performance, as measured by metric j, from the time the model became warm (IsWarm is 1).

• Window: Element j is the model performance, as measured by metric j, evaluated over all observations within the window specified by the MetricsWindowSize property. The software updates Window after it processes MetricsWindowSize observations.

Rows are labeled by the specified metrics. For details, see the Metrics name-value argument of incrementalLearner or incrementalRegressionLinear.

Data Types: table

MetricsWarmupPeriod — Number of observations fit before tracking performance metrics

nonnegative integer

This property is read-only.

Number of observations the incremental model must be fit to before it tracks performance metrics in its Metrics property, specified as a nonnegative integer.

The default MetricsWarmupPeriod value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the MetricsWarmupPeriod name-value argument of the incrementalLearner function sets this property. The default value of the argument is 0.

• Otherwise, the default value is 1000.

For more details, see Performance Metrics.

Data Types: single | double

MetricsWindowSize — Number of observations to use to compute window performance metrics

positive integer

This property is read-only.

Number of observations to use to compute window performance metrics, specified as a positive integer.

The default MetricsWindowSize value depends on how you create the model:

• If you convert a traditionally trained model to create Mdl, the MetricsWindowSize name-value argument of the incrementalLearner function sets this property. The default value of the argument is 200.

• Otherwise, the default value is 200.

For more details on performance metrics options, see Performance Metrics.

Data Types: single | double

Object Functions

fit	Train linear model for incremental learning
updateMetricsAndFit	Update performance metrics in linear incremental learning model given new data and train model
updateMetrics	Update performance metrics in linear incremental learning model given new data
loss	Loss of linear incremental learning model on batch of data
predict	Predict responses for new observations from linear incremental learning model
perObservationLoss	Per observation regression error of model for incremental learning
reset	Reset incremental regression model

Examples

Create Incremental Learner Without Any Prior Information

Create a default incremental linear model for regression.

Mdl = incrementalRegressionLinear()

Mdl = 
  incrementalRegressionLinear

               IsWarm: 0
              Metrics: [1x2 table]
    ResponseTransform: 'none'
                 Beta: [0x1 double]
                 Bias: 0
              Learner: 'svm'

Mdl.EstimationPeriod

ans = 
1000

Mdl is an incrementalRegressionLinear model object. All its properties are read-only.

Mdl must be fit to data before you can use it to perform any other operations. The software sets the estimation period to 1000 because half the width of the epsilon insensitive band Epsilon is unknown. You can set Epsilon to a positive floating-point scalar by using the Epsilon name-value argument. This action results in a default estimation period of 0.

Load the robot arm data set.

load robotarm

For details on the data set, enter Description at the command line.

Fit the incremental model to the training data by using the updateMetricsAndFit function. To simulate a data stream fit the model in chunks of 50 observations at a time. At each iteration:

• Process 50 observations.

• Overwrite the previous incremental model with a new one fitted to the incoming observations.

• Store ${\beta }_1$, the cumulative metrics, and the window metrics to see how they evolve during incremental learning.

% Preallocation
n = numel(ytrain);
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ei = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta1 = zeros(nchunk+1,1);    

% Incremental fitting
rng("default"); % For reproducibility
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,Xtrain(idx,:),ytrain(idx));
    ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:};
    beta1(j + 1) = Mdl.Beta(1);
end

Mdl is an incrementalRegressionLinear model object trained on all the data in the stream. While updateMetricsAndFit processes the first 1000 observations, it stores the response values to estimate Epsilon; the function does not fit the coefficients until after this estimation period. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.

To see how the performance metrics and ${\beta }_1$ evolve during training, plot them on separate tiles.

t = tiledlayout(2,1);
nexttile
plot(beta1)
ylabel('\beta_1')
xlim([0 nchunk])
xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.')
nexttile
h = plot(ei.Variables);
xlim([0 nchunk])
ylabel('Epsilon Insensitive Loss')
xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.')
xline((Mdl.EstimationPeriod + Mdl.MetricsWarmupPeriod)/numObsPerChunk,'g-.')
legend(h,ei.Properties.VariableNames)
xlabel(t,'Iteration')

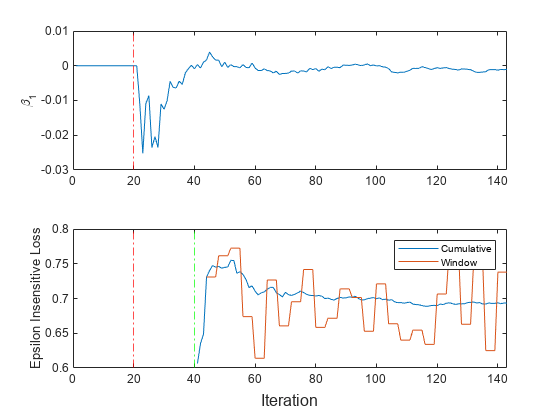
The plot suggests that updateMetricsAndFit does the following:

• After the estimation period (first 20 iterations), fit ${\beta }_1$ during all incremental learning iterations.

• Compute the performance metrics after the metrics warm-up period only.

• Compute the cumulative metrics during each iteration.

• Compute the window metrics after processing 500 observations (4 iterations).

Configure Incremental Learning Options

Prepare an incremental regression learner by specifying a metrics warm-up period, during which the updateMetricsAndFit function only fits the model. Specify a metrics window size of 500 observations. Train the model by using SGD, and adjust the SGD batch size, learning rate, and regularization parameter.

Load the robot arm data set.

load robotarm
n = numel(ytrain);

For details on the data set, enter Description at the command line.

Create an incremental linear model for regression. Configure the model as follows:

• Specify the SGD solver.

• Assume that these settings work well for the problem: a ridge regularization parameter value of 0.001, SGD batch size of 20, learning rate of 0.002, and half the width of the epsilon insensitive band for SVM of 0.05.

• Specify that the incremental fitting functions process the raw (unstandardized) predictor data.

• Specify a metrics warm-up period of 1000 observations.

• Specify a metrics window size of 500 observations.

• Track the epsilon insensitive loss, MSE, and mean absolute error (MAE) to measure the performance of the model. The software supports epsilon insensitive loss and MSE. Create an anonymous function that measures the absolute error of each new observation. Create a structure array containing the name MeanAbsoluteError and its corresponding function.

maefcn = @(z,zfit)abs(z - zfit);
maemetric = struct("MeanAbsoluteError",maefcn);

Mdl = incrementalRegressionLinear('Epsilon',0.05, ...
    'Solver','sgd','Lambda',0.001,'BatchSize',20,'LearnRate',0.002, ...
    'Standardize',false, ...
    'MetricsWarmupPeriod',1000,'MetricsWindowSize',500, ...
    'Metrics',{'epsiloninsensitive' 'mse' maemetric})

Mdl = 
  incrementalRegressionLinear

               IsWarm: 0
              Metrics: [3x2 table]
    ResponseTransform: 'none'
                 Beta: [0x1 double]
                 Bias: 0
              Learner: 'svm'

Mdl is an incrementalRegressionLinear model object configured for incremental learning without an estimation period.

Fit the incremental model to the data by using the updateMetricsAndFit function. At each iteration:

• Simulate a data stream by processing a chunk of 50 observations. Note that the chunk size is different from SGD batch size.

• Overwrite the previous incremental model with a new one fitted to the incoming observations.

• Store the estimated coefficient ${\beta }_{10}$, the cumulative metrics, and the window metrics to see how they evolve during incremental learning.

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ei = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
mse = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
mae = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta10 = zeros(nchunk+1,1);    

% Incremental fitting
rng("default"); % For reproducibility
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,Xtrain(idx,:),ytrain(idx));
    ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:};
    mse{j,:} = Mdl.Metrics{"MeanSquaredError",:};
    mae{j,:} = Mdl.Metrics{"MeanAbsoluteError",:};
    beta10(j + 1) = Mdl.Beta(10);
end

Mdl is an incrementalRegressionLinear model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.

To see how the performance metrics and ${\beta }_{10}$ evolve during training, plot them on separate tiles.

tiledlayout(2,2)
nexttile
plot(beta10)
ylabel('\beta_{10}')
xlim([0 nchunk])
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
xlabel('Iteration')
nexttile
h = plot(ei.Variables);
xlim([0 nchunk])
ylabel('Epsilon Insensitive Loss')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
legend(h,ei.Properties.VariableNames)
xlabel('Iteration')
nexttile
h = plot(mse.Variables);
xlim([0 nchunk])
ylabel('MSE')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
legend(h,mse.Properties.VariableNames)
xlabel('Iteration')
nexttile
h = plot(mae.Variables);
xlim([0 nchunk])
ylabel('MAE')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
legend(h,mae.Properties.VariableNames)
xlabel('Iteration')

The plot suggests that updateMetricsAndFit does the following:

• Fit ${\beta }_{10}$ during all incremental learning iterations.

• Compute the performance metrics after the metrics warm-up period only.

• Compute the cumulative metrics during each iteration.

• Compute the window metrics after processing 500 observations (10 iterations).

Convert Traditionally Trained Model to Incremental Learner

Train a linear regression model by using fitrlinear, convert it to an incremental learner, track its performance, and fit it to streaming data. Carry over training options from traditional to incremental learning.

Load and Preprocess Data

Load the 2015 NYC housing data set, and shuffle the data. For more details on the data, see NYC Open Data.

load NYCHousing2015
rng(1); % For reproducibility
n = size(NYCHousing2015,1);
idxshuff = randsample(n,n);
NYCHousing2015 = NYCHousing2015(idxshuff,:);

Suppose that the data collected from Manhattan (BOROUGH = 1) was collected using a new method that doubles its quality. Create a weight variable that attributes 2 to observations collected from Manhattan, and 1 to all other observations.

NYCHousing2015.W = ones(n,1) + (NYCHousing2015.BOROUGH == 1);

Extract the response variable SALEPRICE from the table. For numerical stability, scale SALEPRICE by 1e6.

Y = NYCHousing2015.SALEPRICE/1e6;
NYCHousing2015.SALEPRICE = [];

Create dummy variable matrices from the categorical predictors.

catvars = ["BOROUGH" "BUILDINGCLASSCATEGORY" "NEIGHBORHOOD"];
dumvarstbl = varfun(@(x)dummyvar(categorical(x)),NYCHousing2015, ...
    'InputVariables',catvars);
dumvarmat = table2array(dumvarstbl);
NYCHousing2015(:,catvars) = [];

Treat all other numeric variables in the table as linear predictors of sales price. Concatenate the matrix of dummy variables to the rest of the predictor data. Transpose the resulting predictor matrix.

idxnum = varfun(@isnumeric,NYCHousing2015,'OutputFormat','uniform');
X = [dumvarmat NYCHousing2015{:,idxnum}]';

Train Linear Regression Model

Fit a linear regression model to a random sample of half the data.

idxtt = randsample([true false],n,true);
TTMdl = fitrlinear(X(:,idxtt),Y(idxtt),'ObservationsIn','columns', ...
    'Weights',NYCHousing2015.W(idxtt))

TTMdl = 
  RegressionLinear
         ResponseName: 'Y'
    ResponseTransform: 'none'
                 Beta: [313x1 double]
                 Bias: 0.1116
               Lambda: 2.1977e-05
              Learner: 'svm'

TTMdl is a RegressionLinear model object representing a traditionally trained linear regression model.

Convert Trained Model

Convert the traditionally trained linear regression model to a linear regression model for incremental learning.

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalRegressionLinear

               IsWarm: 1
              Metrics: [1x2 table]
    ResponseTransform: 'none'
                 Beta: [313x1 double]
                 Bias: 0.1116
              Learner: 'svm'

Separately Track Performance Metrics and Fit Model

Perform incremental learning on the rest of the data by using the updateMetrics and fit functions. Simulate a data stream by processing 500 observations at a time. At each iteration:

1. Call updateMetrics to update the cumulative and window epsilon insensitive loss of the model given the incoming chunk of observations. Overwrite the previous incremental model to update the losses in the Metrics property. Note that the function does not fit the model to the chunk of data—the chunk is "new" data for the model. Specify that the observations are oriented in columns, and specify the observation weights.

2. Call fit to fit the model to the incoming chunk of observations. Overwrite the previous incremental model to update the model parameters. Specify that the observations are oriented in columns, and specify the observation weights.

3. Store the losses and last estimated coefficient ${\beta }_{313}$.

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 500;
nchunk = floor(nil/numObsPerChunk);
ei = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta313 = [IncrementalMdl.Beta(end); zeros(nchunk,1)];
Xil = X(:,idxil);
Yil = Y(idxil);
Wil = NYCHousing2015.W(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(:,idx),Yil(idx), ...
        'ObservationsIn','columns','Weights',Wil(idx));
    ei{j,:} = IncrementalMdl.Metrics{"EpsilonInsensitiveLoss",:};
    IncrementalMdl = fit(IncrementalMdl,Xil(:,idx),Yil(idx),'ObservationsIn','columns', ...
        'Weights',Wil(idx));
    beta313(j + 1) = IncrementalMdl.Beta(end);
end

IncrementalMdl is an incrementalRegressionLinear model object trained on all the data in the stream.

Alternatively, you can use updateMetricsAndFit to update performance metrics of the model given a new chunk of data, and then fit the model to the data.

Plot a trace plot of the performance metrics and estimated coefficient ${\beta }_{313}$.

t = tiledlayout(2,1);
nexttile
h = plot(ei.Variables);
xlim([0 nchunk])
ylabel('Epsilon Insensitive Loss')
legend(h,ei.Properties.VariableNames)
nexttile
plot(beta313)
ylabel('\beta_{313}')
xlim([0 nchunk])
xlabel(t,'Iteration')

The cumulative loss gradually changes with each iteration (chunk of 500 observations), whereas the window loss jumps. Because the metrics window is 200 by default, updateMetrics measures the performance based on the latest 200 observations in each 500 observation chunk.

${\beta }_{313}$ changes abruptly, then levels off as fit processes chunks of observations.

More About

Incremental Learning

Incremental learning, or online learning, is a branch of machine learning concerned with processing incoming data from a data stream, possibly given little to no knowledge of the distribution of the predictor variables, aspects of the prediction or objective function (including tuning parameter values), or whether the observations are labeled. Incremental learning differs from traditional machine learning, where enough labeled data is available to fit to a model, perform cross-validation to tune hyperparameters, and infer the predictor distribution.

Given incoming observations, an incremental learning model processes data in any of the following ways, but usually in this order:

• Predict labels.

• Measure the predictive performance.

• Check for structural breaks or drift in the model.

• Fit the model to the incoming observations.

For more details, see Incremental Learning Overview.

Adaptive Scale-Invariant Solver for Incremental Learning

The adaptive scale-invariant solver for incremental learning, introduced in [1], is a gradient-descent-based objective solver for training linear predictive models. The solver is hyperparameter free, insensitive to differences in predictor variable scales, and does not require prior knowledge of the distribution of the predictor variables. These characteristics make it well suited to incremental learning.

The standard SGD and ASGD solvers are sensitive to differing scales among the predictor variables, resulting in models that can perform poorly. To achieve better accuracy using SGD and ASGD, you can standardize the predictor data, and tune the regularization and learning rate parameters. For traditional machine learning, enough data is available to enable hyperparameter tuning by cross-validation and predictor standardization. However, for incremental learning, enough data might not be available (for example, observations might be available only one at a time) and the distribution of the predictors might be unknown. These characteristics make parameter tuning and predictor standardization difficult or impossible to do during incremental learning.

The incremental fitting functions for regression fit and updateMetricsAndFit use the more conservative ScInOL1 version of the algorithm.

Tips

• After creating a model, you can generate C/C++ code that performs incremental learning on a data stream. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.

Algorithms

Estimation Period

During the estimation period, the incremental fitting functions fit and updateMetricsAndFit use the first incoming EstimationPeriod observations to estimate (tune) hyperparameters required for incremental training. Estimation occurs only when EstimationPeriod is positive. This table describes the hyperparameters and when they are estimated, or tuned.

Hyperparameter	Model Property	Usage	Conditions
Predictor means and standard deviations	Mu and Sigma	Standardize predictor data	The hyperparameters are estimated when both of these conditions apply: Incremental fitting functions are configured to standardize predictor data (see Standardize Data). Mdl.Mu and Mdl.Sigma are empty arrays [].
Learning rate	LearnRate	Adjust the solver step size	The hyperparameter is estimated when both of these conditions apply: The solver is SGD or ASGD (see Solver). You do not specify the 'LearnRate' name-value argument as a positive scalar.
Half the width of the epsilon insensitive band	Epsilon	Control the number of support vectors	The hyperparameter is estimated when both of these conditions apply: The learner is SVM (see Learner). You do not specify the 'Epsilon' name-value argument as a nonnegative scalar.

During the estimation period, fit does not fit the model, and updateMetricsAndFit does not fit the model or update the performance metrics. At the end of the estimation period, the functions update the properties that store the hyperparameters.

Standardize Data

If incremental learning functions are configured to standardize predictor variables, they do so using the means and standard deviations stored in the Mu and Sigma properties of the incremental learning model Mdl.

• When you set 'Standardize',true and a positive estimation period (see EstimationPeriod), and Mdl.Mu and Mdl.Sigma are empty, incremental fitting functions estimate means and standard deviations using the estimation period observations.

• When you set 'Standardize','auto' (the default), the following conditions apply.

  • If you create incrementalRegressionLinear by converting a traditionally trained SVM regression model (CompactRegressionSVM or RegressionSVM), and the Mu and Sigma properties of the model being converted are empty arrays [], incremental learning functions do not standardize predictor variables. If the Mu and Sigma properties of the model being converted are nonempty, incremental learning functions standardize the predictor variables using the specified means and standard deviations. Incremental fitting functions do not estimate new means and standard deviations regardless of the length of the estimation period.

  • If you create incrementalRegressionLinear by converting a linear regression model (RegressionLinear), incremental learning functions does not standardize the data regardless of the length of the estimation period.

  • If you do not convert a traditionally trained model, incremental learning functions standardize the predictor data only when you specify an SGD solver (see Solver) and a positive estimation period (see EstimationPeriod).

• When incremental fitting functions estimate predictor means and standard deviations, the functions compute weighted means and weighted standard deviations using the estimation period observations. Specifically, the functions standardize predictor j (x_j) using

  $$x_j^{\ast }=\frac{x_j-{\mu }_j^{\ast }}{{\sigma }_j^{\ast }}.$$

  • x_j is predictor j, and x_jk is observation k of predictor j in the estimation period.

  • $${\mu }_j^{\ast }=\frac{1}{{\displaystyle \sum _k{w}_k}}{\displaystyle \sum _k{w}_k{x}_{jk}}.$$

  • $${\left({\sigma }_j^{\ast }\right)}^2=\frac{1}{{\displaystyle \sum _k{w}_k}}{\displaystyle \sum _k{w}_k{\left(x_{jk}-{\mu }_j^{\ast }\right)}^2}.$$

  • w_j is observation weight j.

Performance Metrics

• The updateMetrics and updateMetricsAndFit functions track model performance metrics ('Metrics') from new data when the incremental model is warm (IsWarm property). An incremental model becomes warm after fit or updateMetricsAndFit fit the incremental model to MetricsWarmupPeriod observations, which is the metrics warm-up period.

  If EstimationPeriod > 0, the functions estimate hyperparameters before fitting the model to data. Therefore, the functions must process an additional EstimationPeriod observations before the model starts the metrics warm-up period.

• The Metrics property of the incremental model stores two forms of each performance metric as variables (columns) of a table, Cumulative and Window, with individual metrics in rows. When the incremental model is warm, updateMetrics and updateMetricsAndFit update the metrics at the following frequencies:

  • Cumulative — The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.

  • Window — The functions compute metrics based on all observations within a window determined by the MetricsWindowSize name-value pair argument. MetricsWindowSize also determines the frequency at which the software updates Window metrics. For example, if MetricsWindowSize is 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:) and Y((end – 20 + 1):end)).

    Incremental functions that track performance metrics within a window use the following process:

    1. Store a buffer of length MetricsWindowSize for each specified metric, and store a buffer of observation weights.

    2. Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.

    3. When the buffer is filled, overwrite Mdl.Metrics.Window with the weighted average performance in the metrics window. If the buffer is overfilled when the function processes a batch of observations, the latest incoming MetricsWindowSize observations enter the buffer, and the earliest observations are removed from the buffer. For example, suppose MetricsWindowSize is 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.

• The software omits an observation with a NaN prediction when computing the Cumulative and Window performance metric values.

References

[1] Kempka, Michał, Wojciech Kotłowski, and Manfred K. Warmuth. "Adaptive Scale-Invariant Online Algorithms for Learning Linear Models." Preprint, submitted February 10, 2019. https://arxiv.org/abs/1902.07528.

[2] Langford, J., L. Li, and T. Zhang. “Sparse Online Learning Via Truncated Gradient.” J. Mach. Learn. Res., Vol. 10, 2009, pp. 777–801.

[3] Shalev-Shwartz, S., Y. Singer, and N. Srebro. “Pegasos: Primal Estimated Sub-Gradient Solver for SVM.” Proceedings of the 24th International Conference on Machine Learning, ICML ’07, 2007, pp. 807–814.

[4] Xu, Wei. “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent.” CoRR, abs/1107.2490, 2011.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• All object functions of an incrementalRegressionLinear model object support code generation.

• If you configure Mdl to shuffle data (see Solver and Shuffle), the fit function randomly shuffles each incoming batch of observations before it fits the model to the batch. The order of the shuffled observations might not match the order generated by MATLAB.

• When you generate code that loads or creates an incrementalRegressionLinear model object, the NumPredictors property must reflect the number of predictor variables.

For more information, see Introduction to Code Generation.

Version History

Introduced in R2020b