Cox

Create Cox model object for lifetime probability of default

Since R2021b

Description

Create and analyze a Cox model object to calculate lifetime probability of default (PD) using this workflow:

1. Use fitLifetimePDModel to create a Cox model object.

2. Optionally, use discardResiduals to remove residual information from the Cox model object.

3. Use predict to predict the conditional PD and predictLifetime to predict the lifetime PD.

4. Use modelDiscrimination to return AUROC and ROC data. You can plot the results using modelDiscriminationPlot.

5. Use modelCalibration to return the root mean square error (RMSE) of observed and predicted PD data. You can plot the results using modelCalibrationPlot.

Creation

Syntax

CoxPDModel = fitLifetimePDModel(data,ModelType,AgeVar=agevar_value)

CoxPDModel = fitLifetimePDModel(___,Name=Value)

Description

CoxPDModel = fitLifetimePDModel(data,ModelType,AgeVar=agevar_value) creates a Cox PD model object.

If you do not specify variable information for IDVar, LoanVars, MacroVars, and ResponseVar, then:

• IDVar is set to the first column in the data input.

• LoanVars is set to include all columns from the second to the second-to-last columns of the data input.

• ResponseVar is set to the last column in the data input.

CoxPDModel = fitLifetimePDModel(___,Name=Value) sets optional properties using additional name-value arguments in addition to the required arguments in the previous syntax. For example, CoxPDModel = fitLifetimePDModel(data(TrainDataInd,:),"Cox",ModelID="Cox_A",Description="Cox_model",AgeVar="YOB",IDVar="ID",LoanVars="ScoreGroup",MacroVars={'GDP','Market'},ResponseVar="Default",TimeInterval=1,TieBreakMethod="Efron",WeightsVar="Weights") creates a CoxPDModel using a Cox model type. You can specify multiple name-value arguments.

Input Arguments

data — Data

table

Data, specified as a table, in panel data form. The data must contain an ID column and an Age column. The response variable must be a binary variable with the value 0 or 1, with 1 indicating default.

Data Types: table

ModelType — Model type

string with value "Cox" | character vector with value 'Cox'

Model type, specified as a string with the value "Cox" or a character vector with the value 'Cox'.

Data Types: char | string

Name-Value Arguments

Specify required and optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: CoxPDModel = fitLifetimePDModel(data(TrainDataInd,:),"Cox",ModelID="Cox_A",Description="Cox_model",AgeVar="YOB",IDVar="ID",LoanVars="ScoreGroup",MacroVars={'GDP','Market'},ResponseVar="Default",TimeInterval=1,WeightsVar="Weights")

Required Cox Name-Value Argument

AgeVar — Age variable indicating which column in data contains loan age information

string | character vector

Age variable indicating which column in data contains the loan age information, specified as AgeVar and a string or character vector.

Note

The required name-value argument AgeVar is not treated as a predictor in the Cox lifetime PD model. When using a Cox model, you must specify predictor variables using LoanVars or MacroVars. The AgeVar values are the event times for the underlying Cox proportional hazards model.

AgeVar values for each ID should be increasing. If there are nonpositive age increments, fitLifetimePDModel warns when you create a Cox model and removes the IDs with nonpositive age increments. By default, the TimeInterval value is set to the most common age increment in the training data.

Data Types: string | char

Optional Cox Name-Value Arguments

ModelID — User-defined model ID

Cox (default) | string | character vector

User-defined model ID, specified as ModelID and a string or character vector. The software uses the ModelID to format outputs and is expected to be short.

Data Types: string | char

Description — User-defined description for model

"" (default) | string | character vector

User-defined description for model, specified as Description and a string or character vector.

Data Types: string | char

IDVar — ID variable indicating which column in data contains loan or borrower ID

1st column of data (default) | string | character vector

ID variable indicating which column in data contains the loan or borrower ID, specified as IDVar and a string or character vector.

Data Types: string | char

LoanVars — Loan variables indicating which column in data contains loan-specific information

all columns of data that are not the first or last column (default) | string array | cell array of character vectors

Loan variables indicating which column in data contains the loan-specific information, such as origination score or loan-to-value ratio, specified as LoanVars and a string array or cell array of character vectors.

Data Types: string | cell

MacroVars — Macro variables indicating which column in data contains macroeconomic information

"" (default) | string array | cell array of character vectors

Macro variables indicating which column in data contains the macroeconomic information, such as gross domestic product (GDP) growth or unemployment rate, specified as MacroVars and a string array or cell array of character vectors.

Data Types: string | cell

ResponseVar — Variable indicating which column in data contains response variable

string | character vector

Variable indicating which column in data contains the response variable, specified as ResponseVar and a logical value.

Note

The response variable values in the data must be a binary variable with 0 or 1 values, with 1 indicating default.

In Cox lifetime PD models, the ResponseVar values define the censoring information for the underlying Cox proportional hazards model.

Data Types: string | char

WeightsVar — Column name containing weights

"" (default) | string array

Column name of the input table containing weights, specified as a string scalar.

Note

The default value ("") results in a weight of 1 for each row in data. All weight values in data must be nonnegative.

For an example using WeightsVar, see Create Weighted Lifetime PD Model.

Data Types: string

TimeInterval — Time interval value

set to most common AgeVar increment in the training data (default) | positive numeric scalar

Time interval value, specified as a positive numeric scalar indicating the time interval used to define the 0-1 default indicator values in the response variable. The time interval typically coincides with the distance between age values in training data in the panel data input. For example, if the age data (AgeVar) is 1, 2, 3, ..., then the TimeInterval is 1; if the age data is 0.25, 0.5, 0.75,..., then the TimeInterval is 0.25. For more information, see Time Interval for Cox Models and Lifetime Prediction and Time Interval. For Cox models, the TimeInterval value is necessary to fit time-dependent models and also for the PD computation when you use the predict function.

Note

Unlike Logistic and Probit models, a Cox model requires an AgeVar variable. By default, if you do not specify a TimeInterval when creating a Cox model, the TimeInterval is inferred from the increments in the AgeVar values in the training data.

Data Types: double

TieBreakMethod — Method to handle tied default times

"breslow" (default) | string with value "breslow" or "efron" | character vector with value 'breslow' or 'efron'

Since R2023a

Method to handle tied default times, specified as a string or character vector with one of the following tie-break methods:

• breslow — Breslow's approximation to the partial likelihood

• efron — Efron's approximation to the partial likelihood

For credit applications, the time to default comes discretized and there are many "ties." This means that are multiple borrowers that may default at the same (discretized) time (such as, in the second year of their loan). TieBreakMethod supports the breslow or efron methods to handle this scenario.

Data Types: string | char

Properties

ModelID — User-defined model ID

Probit (default) | string

User-defined model ID, returned as a string.

Data Types: string

Description — User-defined description

"" (default) | string

User-defined description, returned as a string.

Data Types: string

UnderlyingModel — Underlying statistical model

Cox model

Underlying statistical model, returned as a returned as a Cox proportional hazards model object. For more information, see fitcox and CoxModel.

Data Types: CoxModel

IDVar — ID variable indicating which column in data contains loan or borrower ID

1st column of data (default) | string

ID variable indicating which column in data contains the loan or borrower ID, returned as a string.

Data Types: string

AgeVar — Age variable indicating which column in data contains loan age information

string

Age variable indicating which column in data contains the loan age information, returned as a string.

Data Types: string

LoanVars — Loan variables indicating which column in data contains loan-specific information

all columns of data that are not the first or last column (default) | string array

Loan variables indicating which column in data contains the loan-specific information, returned as a string array.

Data Types: string

MacroVars — Macro variables indicating which column in data contains macroeconomic information

"" (default) | string array

Macro variables indicating which column in data contains the macroeconomic information, returned as a string array.

Data Types: string

ResponseVar — Variable indicating which column in data contains response variable

string

Variable indicating which column in data contains the response variable, returned as a string.

Data Types: string

WeightsVar — Column name containing weights

"" (default) | string scalar

Column name of the input table containing weights, returned as a string scalar.

Data Types: string

TimeInterval — Time interval value

positive numeric scalar

This property is read-only.

Time interval value, returned as a positive numeric scalar.

Data Types: double

ExtrapolationFactor — Extrapolation factor

1 (default) | positive numeric between 0 and 1

Extrapolation factor, returned as a positive numeric scalar between 0 and 1.

By default, the ExtrapolationFactor is set to 1. For age values (AgeVar) greater than the maximum age observed in the training data, the conditional PD, computed with predict, uses the maximum age observed in the training data. In particular, the predicted PD value is constant if the predictor values do not change and only the age values change when the ExtrapolationFactor is 1. For more information, see Extrapolation for Cox Models, Extrapolation Factor for Cox Models, and Use Cox Lifetime PD Model to Predict Conditional PD.

Data Types: double

TieBreakMethod — Method to handle tied default times

"breslow" (default) | string with value "breslow" or "efron"

Method to handle tied default times, returned as a string.

Data Types: string

Object Functions

predict	Compute conditional PD
predictLifetime	Compute cumulative lifetime PD, marginal PD, and survival probability
modelDiscrimination	Compute AUROC and ROC data
modelCalibration	Compute RMSE of predicted and observed PDs on grouped data
modelDiscriminationPlot	Plot ROC curve
modelCalibrationPlot	Plot observed default rates compared to predicted PDs on grouped data
discardResiduals	Discard residual information of underlying Cox model

Examples

Create Cox Lifetime PD Model

This example shows how to use fitLifetimePDModel to create a Cox model using credit and macroeconomic data.

Load Data

Load the credit portfolio data.

load RetailCreditPanelData.mat
disp(head(data))

    ID    ScoreGroup    YOB    Default    Year
    __    __________    ___    _______    ____

    1      Low Risk      1        0       1997
    1      Low Risk      2        0       1998
    1      Low Risk      3        0       1999
    1      Low Risk      4        0       2000
    1      Low Risk      5        0       2001
    1      Low Risk      6        0       2002
    1      Low Risk      7        0       2003
    1      Low Risk      8        0       2004

disp(head(dataMacro))

    Year     GDP     Market
    ____    _____    ______

    1997     2.72      7.61
    1998     3.57     26.24
    1999     2.86      18.1
    2000     2.43      3.19
    2001     1.26    -10.51
    2002    -0.59    -22.95
    2003     0.63      2.78
    2004     1.85      9.48

Join the two data components into a single data set.

data = join(data,dataMacro);
disp(head(data))

    ID    ScoreGroup    YOB    Default    Year     GDP     Market
    __    __________    ___    _______    ____    _____    ______

    1      Low Risk      1        0       1997     2.72      7.61
    1      Low Risk      2        0       1998     3.57     26.24
    1      Low Risk      3        0       1999     2.86      18.1
    1      Low Risk      4        0       2000     2.43      3.19
    1      Low Risk      5        0       2001     1.26    -10.51
    1      Low Risk      6        0       2002    -0.59    -22.95
    1      Low Risk      7        0       2003     0.63      2.78
    1      Low Risk      8        0       2004     1.85      9.48

Partition Data

Separate the data into training and test partitions.

nIDs = max(data.ID);
uniqueIDs = unique(data.ID);

rng('default'); % For reproducibility
c = cvpartition(nIDs,'HoldOut',0.4);

TrainIDInd = training(c);
TestIDInd = test(c);

TrainDataInd = ismember(data.ID,uniqueIDs(TrainIDInd));
TestDataInd = ismember(data.ID,uniqueIDs(TestIDInd));

Create a Cox Lifetime PD Model

Use fitLifetimePDModel to create a Cox model using the training data.

pdModel = fitLifetimePDModel(data(TrainDataInd,:),"Cox",...
    AgeVar="YOB", ...
    IDVar="ID", ...
    LoanVars="ScoreGroup", ...
    MacroVars={'GDP','Market'}, ...
    ResponseVar="Default");
disp(pdModel)

  Cox with properties:

    ExtrapolationFactor: 1
                ModelID: "Cox"
            Description: ""
        UnderlyingModel: [1x1 CoxModel]
                  IDVar: "ID"
                 AgeVar: "YOB"
               LoanVars: "ScoreGroup"
              MacroVars: ["GDP"    "Market"]
            ResponseVar: "Default"
             WeightsVar: ""
           TimeInterval: 1

Display the underlying model.

disp(pdModel.UnderlyingModel)

Cox Proportional Hazards regression model

                                 Beta          SE         zStat       pValue   
                              __________    _________    _______    ___________

    ScoreGroup_Medium Risk       -0.6794     0.037029    -18.348     3.4442e-75
    ScoreGroup_Low Risk          -1.2442     0.045244    -27.501    1.7116e-166
    GDP                        -0.084533     0.043687     -1.935       0.052995
    Market                    -0.0084411    0.0032221    -2.6198      0.0087991


Log-likelihood: -41742.871

Validate Model

Use modelDiscrimination to measure the ranking of customers by PD.

DataSetChoice = "Testing";
if DataSetChoice=="Training"
    Ind = TrainDataInd;
else
    Ind = TestDataInd;
end

DiscMeasure = modelDiscrimination(pdModel,data(Ind,:),SegmentBy="ScoreGroup")

DiscMeasure=3×1 table
                                    AUROC 
                                   _______

    Cox, ScoreGroup=High Risk      0.64112
    Cox, ScoreGroup=Medium Risk    0.61989
    Cox, ScoreGroup=Low Risk        0.6314

disp(DiscMeasure)

                                    AUROC 
                                   _______

    Cox, ScoreGroup=High Risk      0.64112
    Cox, ScoreGroup=Medium Risk    0.61989
    Cox, ScoreGroup=Low Risk        0.6314

Use modelDiscriminationPlot to visualize the ROC curve.

modelDiscriminationPlot(pdModel,data(Ind,:),SegmentBy="ScoreGroup")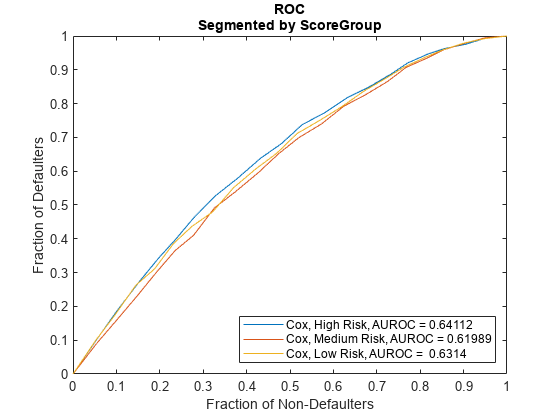

Use modelCalibration to measure the calibration of the predicted PD values. The modelCalibration function requires a grouping variable and compares the accuracy of the observed default rate in the group with the average predicted PD for the group.

CalMeasure = modelCalibration(pdModel,data(Ind,:),{'YOB','ScoreGroup'})

CalMeasure=table
                                         RMSE   
                                       _________

    Cox, grouped by YOB, ScoreGroup    0.0012471

disp(CalMeasure)

                                         RMSE   
                                       _________

    Cox, grouped by YOB, ScoreGroup    0.0012471

Use modelCalibrationPlot to visualize the observed default rates compared to the predicted PD.

modelCalibrationPlot(pdModel,data(Ind,:),{'YOB','ScoreGroup'})

Predict Conditional and Lifetime PD

Use the predict function to predict conditional PD values. The prediction is a row-by-row prediction.

%dataCustomer1 = data(1:8,:);
CondPD = predict(pdModel,data(Ind,:));

Use predictLifetime to predict the lifetime cumulative PD values (computing marginal and survival PD values is also supported).

LifetimePD = predictLifetime(pdModel,data(Ind,:));

Select Tie-Break Method for Cox Lifetime PD Models

Since R2023a

This example shows how to create a Cox model and select the tie-break method while fitting a Cox lifetime PD model.

Load Data

Load the credit portfolio data.

load RetailCreditPanelData.mat
disp(head(data))

    ID    ScoreGroup    YOB    Default    Year
    __    __________    ___    _______    ____

    1      Low Risk      1        0       1997
    1      Low Risk      2        0       1998
    1      Low Risk      3        0       1999
    1      Low Risk      4        0       2000
    1      Low Risk      5        0       2001
    1      Low Risk      6        0       2002
    1      Low Risk      7        0       2003
    1      Low Risk      8        0       2004

disp(head(dataMacro))

    Year     GDP     Market
    ____    _____    ______

    1997     2.72      7.61
    1998     3.57     26.24
    1999     2.86      18.1
    2000     2.43      3.19
    2001     1.26    -10.51
    2002    -0.59    -22.95
    2003     0.63      2.78
    2004     1.85      9.48

Join the two data components into a single data set.

data = join(data,dataMacro);
disp(head(data))

    ID    ScoreGroup    YOB    Default    Year     GDP     Market
    __    __________    ___    _______    ____    _____    ______

    1      Low Risk      1        0       1997     2.72      7.61
    1      Low Risk      2        0       1998     3.57     26.24
    1      Low Risk      3        0       1999     2.86      18.1
    1      Low Risk      4        0       2000     2.43      3.19
    1      Low Risk      5        0       2001     1.26    -10.51
    1      Low Risk      6        0       2002    -0.59    -22.95
    1      Low Risk      7        0       2003     0.63      2.78
    1      Low Risk      8        0       2004     1.85      9.48

Join the Data

Join the two data components into a single data set.

data = join(data,dataMacro);
disp(head(data))

    ID    ScoreGroup    YOB    Default    Year     GDP     Market
    __    __________    ___    _______    ____    _____    ______

    1      Low Risk      1        0       1997     2.72      7.61
    1      Low Risk      2        0       1998     3.57     26.24
    1      Low Risk      3        0       1999     2.86      18.1
    1      Low Risk      4        0       2000     2.43      3.19
    1      Low Risk      5        0       2001     1.26    -10.51
    1      Low Risk      6        0       2002    -0.59    -22.95
    1      Low Risk      7        0       2003     0.63      2.78
    1      Low Risk      8        0       2004     1.85      9.48

Partition the Data

Separate the data into training and test partitions.

nIDs = max(data.ID);
uniqueIDs = unique(data.ID);

rng('default'); % for reproducibility
c = cvpartition(nIDs,'HoldOut',0.4);

TrainIDInd = training(c);
TestIDInd = test(c);

TrainDataInd = ismember(data.ID,uniqueIDs(TrainIDInd));
TestDataInd = ismember(data.ID,uniqueIDs(TestIDInd));

Create a Cox Lifetime PD Model with Breslow's Method

Use fitLifetimePDModel to create a Cox model using the training data. Use the name-value argument TieBreakMethod to set tie-break method to 'breslow'. This is the default choice for this argument.

pdModel1 = fitLifetimePDModel(data(TrainDataInd,:),"Cox",...
ModelID="Cox-Breslow", IDVar="ID", AgeVar="YOB", ...
LoanVars="ScoreGroup", MacroVars={'GDP','Market'}, ...
ResponseVar="Default",TieBreakMethod='breslow');

Display the underlying model.

disp(pdModel1.Model)

Cox Proportional Hazards regression model

                                 Beta          SE         zStat       pValue   
                              __________    _________    _______    ___________

    ScoreGroup_Medium Risk       -0.6794     0.037029    -18.348     3.4442e-75
    ScoreGroup_Low Risk          -1.2442     0.045244    -27.501    1.7116e-166
    GDP                        -0.084533     0.043687     -1.935       0.052995
    Market                    -0.0084411    0.0032221    -2.6198      0.0087991


Log-likelihood: -41742.871

Use predict to predict the conditional PD.

pd1 = predict(pdModel1,data(TestDataInd,:));

Create a Cox Lifetime PD Model with Efron's Method

Use fitLifetimePDModel to create a Cox model using the training data. Use the name-value argument TieBreakMethod to set tie-break method to 'Efron'. This is the default choice for this argument.

pdModel2 = fitLifetimePDModel(data(TrainDataInd,:),"Cox",...
ModelID="Cox-Efron", IDVar="ID", AgeVar="YOB", ...
LoanVars="ScoreGroup", MacroVars={'GDP','Market'}, ...
ResponseVar="Default",TieBreakMethod='efron');

Display the underlying model. The coefficients are only slightly different for this data set.

disp(pdModel2.Model)

Cox Proportional Hazards regression model

                                 Beta          SE         zStat       pValue  
                              __________    _________    _______    __________

    ScoreGroup_Medium Risk       -0.6844     0.037029    -18.483    2.8461e-76
    ScoreGroup_Low Risk          -1.2515     0.045243    -27.662    2.006e-168
    GDP                        -0.084985     0.043691    -1.9452      0.051756
    Market                    -0.0085126    0.0032223    -2.6418     0.0082469


Log-likelihood: -41713.445

Use predict to predict the conditional PD for the second Cox model.

pd2 = predict(pdModel2,data(TestDataInd,:));

Compare Cox Models

The predictions for the two Cox models are almost the same for this data set.

[pd1(1:10) pd2(1:10)]

ans = 10×2

    0.0162    0.0161
    0.0091    0.0090
    0.0081    0.0081
    0.0073    0.0072
    0.0064    0.0064
    0.0072    0.0072
    0.0030    0.0030
    0.0016    0.0016
    0.0162    0.0161
    0.0091    0.0090

For this data set, the model discrimination (modelDiscrimination) does not seem to change with the TieBreakMethod method and the model accuracy (modelCalibration) shows only a negligible difference in RMSE.

modelDiscriminationPlot(pdModel1,data(TestDataInd,:),ReferencePD=pd2,ReferenceID=pdModel2.ModelID)

modelCalibrationPlot(pdModel1,data(TestDataInd,:),'Year',ReferencePD=pd2,ReferenceID=pdModel2.ModelID)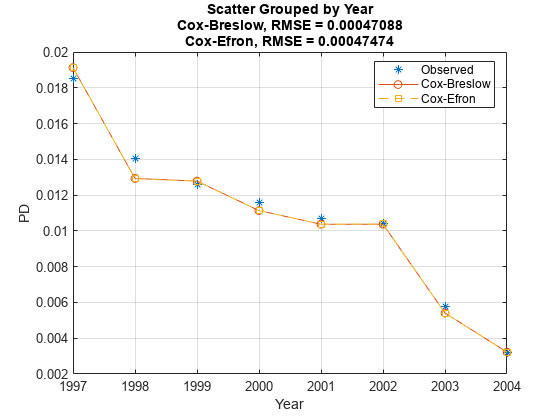

More About

Cox Proportional Hazards Models

The Cox proportional hazards (PH) model is a survival model and it models the time until an event of interest occurs.

For probability of default (PD) models, the event of interest is the default on a credit obligation. Cox models need information on whether there was a default and when it happened. For other commonly used PD models, a binary variable indicating whether there was a default is enough. Cox PD models need that information, plus the age of the loan at the time of default.

The Cox proportional hazards (PH) model, also known as a Cox regression model, assumes the hazard rate is of the form

$$h(t;X)=h_0(t)\exp (X\beta )$$

where

• h₀(t) is the baseline hazard rate.

• X is the predictor data.

• β is a vector of coefficients of the predictors.

• exp(Xβ) is the hazard ratio.

The baseline hazard rate is a reference hazard level, common to all observations, and it does not depend on the predictor values. The hazard ratio is the factor that scales the baseline hazard value up or down, depending on the predictor values. For lower risk observations, the hazard ratio is less than 1 and this reduces the hazard rate. For higher risk observations, the hazard ratio increases the hazard rate.

In the hazard rate formula, the predictor values in X are fixed, or independent of time. This is the basic version of the Cox PH model. For PD models, the basic version of the Cox PH model includes predictors that have constant values, such as the origination score, or whether a property is for residential or commercial purposes.

The time-dependent Cox PH model allows predictor values to change over time. For example, the loan-to-value (LTV) ratio changes over the life of a loan, and the macroeconomic variables change from period to period. Therefore, the following hazard rate formula for time-dependent models includes predictor values that can be a function of time:

$$h(t;X)=h_0(t)\exp (X(t)\beta )$$

The data input for fitLifetimePDModel must be in panel data form. For each ID (IDVar), there are multiple rows of data. The panel data input is required for both time-dependent and time -independent models.

For time-independent predictors, the predictor value is constant for each ID. For example, the score at origination for each customer is constant throughout the life of the loan, and this value is repeated for each row corresponding to the same ID in the panel data format.

For time-dependent predictors, the values may change from one row to the next for the same ID. The assumption is that the predictor values in each row are valid in the time interval defined by the age value (AgeVar) in the previous row and the age value in the current row.

Time Interval for Cox Models

Time is discretized into intervals, and predictor values in the training data (data input) are constant for each interval: X₁ from t₀ to t₁; X₂ from t₁ to t₂; and so forth.

The data input must be in panel data form, with multiple observations for each ID, with corresponding age information (the t_k values, the AgeVar column) and the corresponding default indicator values (the ResponseVar column).

Assume that t_k - t_{k - 1} = Δt for all k and this is the time interval. This time interval is the age increment for consecutive observations in the age data (AgeVar). The assumption is that these increments are regular and that the default indicator (ResponseVar) is defined consistently with this time interval, in the sense that a 1 means there was a default in a time interval of length Δt. The time interval Δt is also used for the computation of the probability of default. For more information, see Survival and Probability of Default for Cox Models. The TimeInterval property is also used to validate the data input to predictLifetime; for more information see Validation of Data Input for Lifetime Prediction and Lifetime Prediction and Time Interval.

Survival and Probability of Default for Cox Models

The survival function S(t) is a function of time, and gives the probability of surviving longer than a given time t.

$$S(t)=P(T>t)$$

where

• T is the failure time, the random variable of interest, and in the Cox model case, the time to default.

• t is the specific time of interest, for example, 1 year.

The main relationship between the survival function and the hazard rate is

$$S(t)=\exp \left(-{\displaystyle {\int }_0^{t}h(u)du}\right)$$

Higher values of the hazard rate cause the survival probability to drop faster. Conversely, lower values of the hazard rate cause the survival probability to rise faster.

The probability of default (PD) is the conditional probability of defaulting in a time interval, given that there has been no default prior to that interval. For example, the probability of default between time s and t, with s < t, is represented as:

$$\begin{array}{l}PD(s,t)=P(s<T\le t|T>s)\\ \text{ = }\frac{S(s)-S(t)}{S(s)}\\ \text{ = 1-}\frac{S(t)}{S(s)}\end{array}$$

In credit applications, the time interval of interest, Δt, is consistent with the training data and the definition of default in the response variable. The PD is a function of a single time variable t and the implicit time interval Δt:

$$PD(t)=1-\frac{S(t)}{S(t-\Delta t)}$$

References

[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.

[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.

[3] Breeden, Joseph. Living with CECL: The Modeling Dictionary. Santa Fe, NM: Prescient Models LLC, 2018.

[4] Roesch, Daniel and Harald Scheule. Deep Credit Risk: Machine Learning with Python. Independently published, 2020.

Version History

Introduced in R2021b

R2023b: Added WeightsVar name-value argument for Cox model

The Cox model supports a WeightsVar name-value argument for observation weights.

R2023a: modelAccuracy object function is renamed to modelCalibration function

The modelAccuracy object function is renamed to modelCalibration function. The use of modelAccuracy is discouraged, use modelCalibration instead.

R2023a: modelAccuracyPlot object function is renamed to modelCalibrationPlot function

The modelAccuracyPlot object function is renamed to modelCalibrationPlot function. The use of modelAccuracyPlot is discouraged, use modelCalibrationPlot instead.

R2023a: Added TieBreakMethod name-value argument

The TieBreakMethod name-value argument enables you to specify the method to handle tied default times.

R2023a: Added discardResiduals method for Cox model

Use the discardResiduals method to discard residual information of the underlying Cox model.

R2023a: Model property renamed to UnderlyingModel

The Model property is renamed to UnderlyingModel.