rfsystem

Generate RF Blockset model and perform circuit envelope or idealized baseband simulation

Since R2021a

expand all in page

Description

Use the rfsystem System object™ to generate RF Blockset™ model and perform circuit envelope and idealized baseband (since R2023a) simulation of an RF system designed using an rfbudget object. This object supports vector inputs and has no limitations on the frame size.

Note

You can add or delete RF Blockset blocks from the model but you cannot modify the parameters of the Inport and Outport blocks. After this update, the input rfbudget object to the rfsystem will be preserved and you can inspect this rfbudget object using the RF Budget Analyzer app.

To perform circuit envelope simulation of an RF system:

  1. Create the rfsystem object and set its properties.

  2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

rfs = rfsystem(rfb)
rfs = rfsystem(rfb,Name=Value)

Description

rfs = rfsystem(rfb) generates an RF Blockset model from the RF budget object rfb and perform circuit envelope or idealized baseband (since R2023a) simulation.

Use Object Functions to open, save, close, or hide the RF Blockset model.

example

rfs = rfsystem(rfb,Name=Value) sets Properties using name-value arguments. For example, rfsystem(rfb,'ModelName'='rfmodel') sets the name of the RF Blockset model to rfmodel.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Name of the RF Blockset model, specified as a string scalar or character vector.

Example: 'ModelName','RFModel'

Input frequency for each input in the RF system, specified as a row vector in Hz. The default value of this property is the value you specify in the InputFrequency argument in the rfbudget object.

If the rfb.InputFrequency(1) is set to 0, then in:

  • Circuit Envelope Simulation — Your RF system has two inputs, I and Q, at DC.

  • Idealized Baseband Simulation — Your RF system input is at DC with the I and Q components distributed on the real and imaginary parts of the signal input argument. (since R2023a)

Note

You can set InputFrequency to a vector after creating the System object if you want to investigate the intermodulation of nearby signals using the same model.

Output frequency for each output of the RF system, specified as a row vector in Hz. This output frequency is derived from the RF system designed using an rfbudget object.

If the value of the rfb.OutputFrequency(1) is 0, then in:

  • Circuit Envelope Simulation — Your RF system will have two outputs, I and Q, at DC.

  • Idealized Baseband Simulation — Your RF system output is at DC, with the I and Q components distributed on the real and imaginary components of the signal returned output. (since R2023a)

Time step for circuit envelope simulation, specified as a positive scalar. This property sets the step size between simulations.

Number of input chains in a multiple-input single-output receiver system, specified as a positive scalar.

Note

You can set:

  • Either the 'Rx' or the 'Tx' property when creating the System object.

  • 'Rx' property only when creating the System object.

Number of output chains in a single-input multiple-output transmitter system, specified as a positive scalar.

Note

You can set:

  • Either the 'Rx' or the 'Tx' property when creating the System object.

  • 'Rx' property only when creating the System object.

Number of optional Simulink inputs, specified as a positive scalar. The Simulink inputs are added as Inport (Simulink) block in the model.

By default, the Signal Type parameter in the Simulink Inport blocks is set to complex. To change this complex signal to real, either add a Complex to Real-Imag (Simulink) block to your model, or in the Simulink Inport block, on the Signal Attributes tab set the Signal Type parameter real.

Number of optional Simulink outputs, specified as a positive scalar. The Simulink outputs are added as Outport (Simulink) blocks in the model.

By default, the Signal Type parameter in the Simulink Outport block is set to complex. To change this complex signal to real, either add a Complex to Real-Imag (Simulink) block to your model, or in the Simulink Inport block, on the Signal Attributes tab set the Signal Type parameter real.

This property is read-only.

Number of RF inputs implemented as RF Blockset Inport blocks in the generated model, returned as a nonnegative scalar. The value of this property depends on the 'Rx' property and the first value in the 'InputFrequency' row vector.

This property is read-only.

Number of RF outputs implemented as RF Blockset Outport blocks in the generated model, returned as a nonnegative scalar. The value of this property depends on the 'Tx' property and the last value in the 'OutputFrequency' row vector.

Since R2023a

RF Blockset libraries, specified as one of the following:

  • 'CircuitEnvelope' — Use Circuit Envelope library blocks to perform circuit envelope simulation.

  • 'IdealizedBaseband' — Use Idealized Baseband library blocks to perform idealized baseband simulation.

Note

This property cannot be reset once the system object is created.

Since R2025a

Model impedance mismatch loss between idealized baseband elements and export the RF chain into an RF Budget block, specified as logical false(0) or true(1).

Dependencies

To enable this property, set Library='IdealizedBaseband'.

Usage

Syntax

out = rfs(in)

Description

out = rfs(in) creates an RF Blockset circuit envelope or idealized baseband simulation output out using input signal values in. Pass in as an input argument to an automatically-generated RF Blockset model.

You can design four architectures, RF to RF, DC to RF, RF to DC, and DC to DC, using the rfsystem object. For more information, see Design RF-RF, IQ-RF, RF-IQ, and IQ-IQ Architectures.

Note

Passing multiple input vectors and concatenating the output vectors is equivalent to performing one long simulation with a vertically-concatenated input.

example

Input Arguments

expand all

Time-domain input signal, specified as a scalar or column vectors.

  • Circuit Envelope Simulation — Specify a column vector of N columns, where N is the number of input frequencies in the 'InputFrequency' property.

  • Idealized Baseband Simulation — Specify a scalar because idealized Baseband library only supports one carrier frequency. (since R2023a)

If 'RFInputs' > 1 , 'SLInputs' > 1, or both, pass the inputs to the step function as arguments out = rfs(RFin1,RFin2,...,SLin1,SLin2,...).

Output Arguments

expand all

Time-domain output signal, returned as scalar or column vectors. The out is returned as an array of N column vectors when there are N 'OutputFrequency' values to be computed.

If 'RFOutputs' > 1, 'SLOutputs' > 1,or both, then the outputs are returned by the step function is [RFout1,RFout2,...,SLout1,SLout2,...] = rfs(in).

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

expand all

open_systemOpen RF Blockset model created using rfsystem
save_systemSave RF Blockset model created using rfsystem
close_systemClose RF Blockset model window created using rfsystem
hide_systemHide RF Blockset model window created using rfsystem
load_systemLoad RF Blockset model to memory
RF Budget AnalyzerAnalyze gain, noise figure, IP2, and IP3 of cascaded RF elements and export to RF Blockset

expand all

stepRun System object algorithm
releaseRelease resources and allow changes to System object property values and input characteristics
resetReset internal states of System object

Examples

collapse all

This example uses:

Open Script

Design an RF receiver to perform circuit envelope simulation.

Create fifth- and seventh-order bandpass RF filters.

f1 = rffilter('ResponseType','Bandpass','FilterOrder',5, ...
        'PassbandFrequency',[4.85 5.15]*1e9);
f2 = rffilter('ResponseType','Bandpass','FilterOrder',7, ...
        'PassbandFrequency',[10 130]*1e6);

Create two amplifier objects with 3 dB and 5 dB gain, respectively.

a1 = amplifier('Gain',3,'NF',1.53,'OIP3',35);
a2 = amplifier('Gain',5,'NF',8,'OIP3',37);

Create a modulator with a local frequency of 4.93 GHz.

d = modulator('Gain',0,'NF',4,'OIP3',50,'LO',4.93e9, ...
        'ConverterType','Down');

Design an RF receiver with the budget elements at an input frequency of 5 GHz, an available input power of -30 dBm, and a bandwidth of 200 MHz.

rfb = rfbudget([f1 a1 d f2 a2],5e9,-30,200e6);

Create an RF system for the RF receiver using the rfbudget object.

rfs = rfsystem(rfb);

Specify input time-domain signal for the RF system.

in = [1e-3*ones(8,1); zeros(8,1)] .* ones(1,10);
in = in(:);

Calculate the output time-domain signal of the RF system.

out = rfs(in);
out = [out; rfs(in)];

Specify the sample time of the RF system.

t = rfs.SampleTime*(0:length(out)-1);

Plot the simulated output.

plot(t,[in; in],'-o',t,abs(out),'-+')
grid on

Release system resources and turn off fast restart.

release(rfs)

Open an RF Blockset model of the designed RF system using the open_system object function.

open_system(rfs)

This example uses:

Open Script

Design four different chain architectures using an RF System object.

Create an input column vector.

in = (1:8)';

Design RF-RF Architecture

Create an rfbudget object using an amplifier object.

a = amplifier;

Calculate the RF budget of the amplifier at an input frequency of 5 GHz, an available input power of –30 dBm, and a bandwidth of 10 KHz.

rfb = rfbudget(a,5e9,-30,10e3);

Create an RF system using the rfbudget object.

rfs = rfsystem(rfb);

Create an RF-RF architecture using the input column vector.

out0 = rfs(in);

Release system resources and turn off fast restart.

release(rfs)

Open an RF Blockset model of the RF system.

open_system(rfs)

Design IQ-RF Architecture

Use a modulator object with an up converter to create an rfbudget object.

u = modulator('ConverterType','Up','LO',1e9);

Calculate the RF budget of the modulator at an input frequency of 0 GHz, an available input power of –30 dBm, and a bandwidth of 10 KHz.

rfb2 = rfbudget(u,0,-30,10e3);

Create an RF system using the rfbudget object.

rfs2 = rfsystem(rfb2);

Create an IQ-RF architecture using the input column vector.

inI = in;
inQ = in;
out = rfs2(inI,inQ);

Release system resources and turn off fast restart.

release(rfs2)

Open an RF Blockset model of the RF system.

open_system(rfs2)

Design RF-IQ Architecture

Use a modulator object with a down converter to create an rfbudget object.

d = modulator('ConverterType','Down','LO',1e9);

Calculate the RF budget of the modulator at an input frequency of 1 GHz, an available input power of –30 dBm, and a bandwidth of 10 KHz.

rfb3 = rfbudget(d,1e9,-30,10e3);

Create an RF system using the rfbudget object.

rfs3 = rfsystem(rfb3);

Create an RF-IQ architecture using the input column vector.

[outI,outQ] = rfs3(in);

Release system resources and turn off fast restart.

release(rfs3)

Open an RF Blockset model of the RF system.

open_system(rfs3)

Design IQ-IQ Architecture

Create an rfbudget object using an amplifier object.

a1 = amplifier;

Calculate the RF budget of the amplifier at an input frequency of 0 GHz, an available input power of –30 dBm, and a bandwidth of 10 KHz.

rfb4 = rfbudget(a1,0,-30,10e3);

Create an RF system using the rfbudget object.

rfs4 = rfsystem(rfb4);

Create an IQ-IQ architecture using the input column vector.

[outI2,outQ2] = rfs4(inI,inQ);

Release system resources and turn off fast restart.

release(rfs4)

Open an RF Blockset model of the RF system.

open_system(rfs4)

This example uses:

Open Script

Create a fifth-order bandpass RF filter.

f1 = rffilter('ResponseType','Bandpass','FilterOrder',5, ...
   'PassbandFrequency',[4.85 5.15]*1e9);

Create an amplifier with 3 dB gain.

a1 = amplifier('Gain',3,'NF',1.53,'OIP3',35);

Create a modulator with a local frequency of 4.93 GHz.

d = modulator('Gain',0,'NF',4,'OIP3',50,'LO',4.93e9, ...
   'ConverterType','Down');

Create a seventh-order bandpass RF filter.

f2 = rffilter('ResponseType','Bandpass','FilterOrder',7, ...
   'PassbandFrequency',[10 130]*1e6);

Create another amplifier with a 3 dB gain.

a2 = amplifier('Gain',5,'NF',8,'OIP3',37);

Design an RF receiver with the budget elements at an input frequency of 5 GHz, an available input power of –30 dBm, and a bandwidth of 200 MHz.

b = rfbudget([f1 a1 d f2 a2],5e9,-30,200e6);

Duplicate the budget chain into a multiple-input single-output receiver (MISO) system with four branches.

rfs = rfsystem(b,Rx=4);

Open the underlying RF system model to inspect the MISO receiver

open_system(rfs)


set_param(bdroot,'ZoomFactor','FitSystem')

Create four inputs to the MISO receiver. The pulsed carrier square wave input is time-sliced into four pieces.

in1 = [1e-3*[1;1;0;0;0;0;0;0]; zeros(8,1)] .* ones(1,10);
in1 = in1(:);
in2 = [1e-3*[0;0;1;1;0;0;0;0]; zeros(8,1)] .* ones(1,10);
in2 = in2(:);
in3 = [1e-3*[0;0;0;0;1;1;0;0]; zeros(8,1)] .* ones(1,10);
in3 = in3(:);
in4 = [1e-3*[0;0;0;0;0;0;1;1]; zeros(8,1)] .* ones(1,10);
in4 = in4(:);
out = rfs(in1,in2,in3,in4);

Release system resources and turn off fast restart.

release(rfs)
reset(rfs)

Plot the circuit envelope simulated result.

t = rfs.SampleTime*(0:length(out)-1);
plot(t,in1+in2+in3+in4,'-o',t,abs(out),'-+')
grid on

Type rfBudgetAnalyzer(rfs) command at the command line to open the MISO receiver in the RF Budget Analyzer app to visualize the initial budget chain b.

Duplicate the budget chain into a single-input multiple-output (SIMO) array system with sixteen branches.

rfs2 = rfsystem(b,Tx=16);

Open the underlying RF system model to inspect the SIMO receiver

open_system(rfs2)

Type this command at the MATLAB® command line to create 16 outputs to the SIMO transmitter.

[out1(1:16).val] = rfs2(in1);

This example uses:

Open Script

Create a fifth-order bandpass RF filter.

f1 = rffilter('ResponseType','Bandpass','FilterOrder',5,'PassbandFrequency',[4.85 5.15]*1e9);

Create an amplifier with the gain of 3 dB, noise figure of 1.53 dB, and OIP3 of 35 dBm.

a1 = amplifier('Gain',3,'NF',1.53,'OIP3',35);

Create an rfbudget object using these elements at an input frequency of 5 GHz, an available input power of -30 dBm, and a bandwidth of 200 MHz.

rfb = rfbudget([f1 a1],5e9,-30,200e6);

Create an RF system using the rfbdget object. Name the model and save the RF Blockset model.

rfs = rfsystem(rfb,'ModelName','myRFSystem_Model')
save_system(rfs);

rfs = 

  rfsystem with properties:

          ModelName: 'myRFSystem_Model'
         SampleTime: 6.2500e-10
     InputFrequency: 5.0000e+09
    OutputFrequency: 5.0000e+09
           RFInputs: 1
          RFOutputs: 1
            Library: 'CircuitEnvelope'

This example uses:

Open Script

Design an RF receiver using the rfsystem system object. View the object in the RF Budget Analyzer app to perform harmonic balance (HB) analysis.

Create fifth- and seventh-order bandpass RF filters.

f1 = rffilter('ResponseType','Bandpass','FilterOrder',5, ...
        'PassbandFrequency',[4.85 5.15]*1e9);
f2 = rffilter('ResponseType','Bandpass','FilterOrder',7, ...
        'PassbandFrequency',[10 130]*1e6);

Create two amplifier objects with 3 dB and 5 dB gain, respectively.

a1 = amplifier('Gain',3,'NF',1.53,'OIP3',35);
a2 = amplifier('Gain',5,'NF',8,'OIP3',37);

Create a modulator with a local frequency of 4.93 GHz.

d = modulator('Gain',0,'NF',4,'OIP3',50,'LO',4.93e9, ...
        'ConverterType','Down');

Design an RF receiver with the budget elements at an input frequency of 5 GHz, an available input power of – 30 dBm, and a bandwidth of 10 MHz.

rfb = rfbudget([f1 a1 d f2 a2],5e9,-30,10e6);

Create an RF system for the RF receiver using the rfbudget object.

rfs = rfsystem(rfb);

Open an RF Blockset model of the designed RF system using the open_system function.

open_system(rfs)

Type rfBudgetAnalyzer(rfs) command at the MATLAB® command line to open this RF system in the RF Budget Analyzer app.

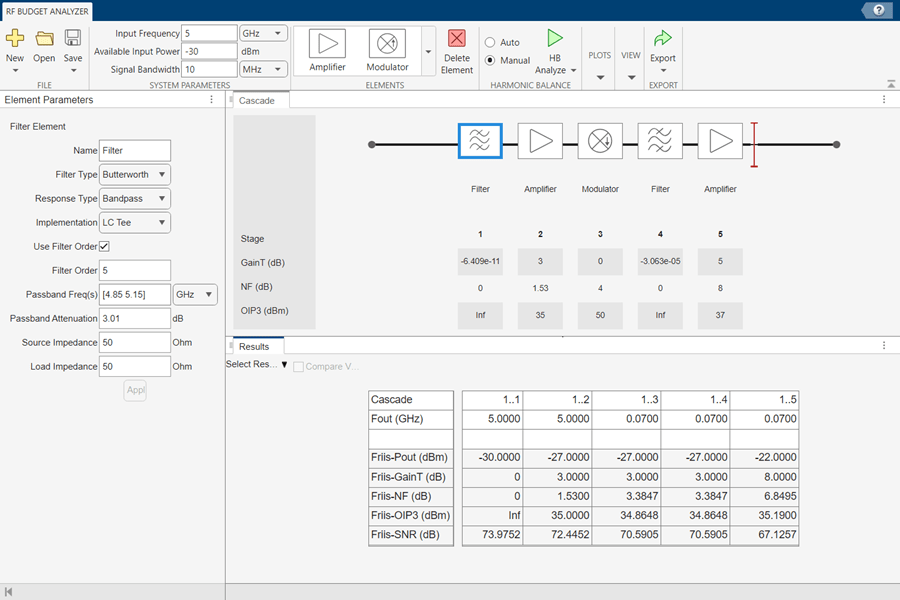
To conduct HB analysis in the app, click the HB-Analyze button.

Since R2025a

This example uses:

Open Script

This example shows you how to account mismatch loss between two elements in an RF chain. To do this:

  • First, define system parameters and construct RF elements.

  • Second, create an rfbudget object to construct an RF chain with the elements that you have designed in the first step and compute its RF budget.

  • Finally, input this rfbudget object to an RF system object to create an RF Blockset model and simulate to account mismatch loss between two elements.

You can choose to simulate your RF chain with either circuit envelope or idealized baseband simulation. This example compares:

  • Simulation fidelity between circuit envelope or idealized baseband simulation.

  • Simulated output with RF budget results.

Define System Parameters

Define input frequency, signal bandwidth, and input power.

fin = 4e9;
bw = 5e6;
in_dBm = -30;

Create RF Elements

Create an amplifier, n-port device, modulator, and RF filter.

a = amplifier( ...
    Gain = 31, ...
    Zin = 41+15i, ...
    Zout = 92+65i);
s = nport('passive.s2p');
m = modulator( ...
    LO = 1e9, ...
    Gain = 42, ...
    Zin = 35+89i, ...
    Zout = 79+32i);
r = rffilter( ...
    PassbandFrequency = fin+1e9-bw/2, ...
    Zin = 38, ...
    Zout = 38);

Create RF Budget and Construct RF Chain

Create rfbudget object and calculate its RF budget.

rfobj = rfbudget([a s m r],fin,in_dBm,bw);

Simulate RF Chain in Circuit Envelope Simulation Environment

Input this budget object to an rfsystem System object™. The rfsystem object enables you to simulate your RF chain using circuit envelope and idealized baseband simulation.

Build your RF chain using circuit envelope simulation. Circuit envelope simulation allows multicarrier simulation of RF networks with arbitrary topology. It also allows impedance mismatches. Estimate the computation time using tic and toc functions.

tic
rfsCE = rfsystem(rfobj);
toc

Elapsed time is 66.067408 seconds.

Open the system modeled using circuit envelope blocks in Simulink.

open_system(rfsCE)

To simulate, first load the MAT file containing the 5G NR baseband input signal.

load('input.mat');
input = input(1:400);

Turn off the noise so that you can compare circuit envelope and idealized baseband simulations.

set_param([rfsCE.ModelName '/Configuration1'],'AddNoise','off')

Define the input signal for rfsystem object.

tic
outCE = rfsCE(input);
tocCE = toc

tocCE =

   21.6998

Simulate RF Chain in Idealized Baseband Simulation Environment

Build your RF chain using idealized baseband simulation. Estimate the computation time using tic and toc functions. This allows you to analyze a cascade of mathematical models of RF components within the MATLAB® environment. The Idealized Baseband System objects assume perfect impedance matching. However, by using Mismatch property in rfsystem System object, you can account for mismatch loss between two elements in an RF chain in your simulation. Estimate the computation time using tic and toc functions.

tic
rfsIdeal = rfsystem(rfobj,'Library','IdealizedBaseband','Mismatch',true);
toc

Elapsed time is 13.137983 seconds.

Open the system modeled using idealized baseband blocks in Simulink.

open_system(rfsIdeal)

Turn off the noise so that you can compare circuit envelope and idealized baseband simulations.

set_param([rfsIdeal.ModelName '/Thermal noise'],'NoiseSrc','None')

tic
outIdeal = rfsIdeal(input);
tocIdeal = toc

tocIdeal =

    4.0277

Plot Simulation Fidelity

Plot the real and imaginary components of the original input signal.

f1 = figure;
subplot(2,1,1),plot(real(input)),title('Real')
subplot(2,1,2),plot(imag(input)),title('Imag')
sgtitle('Original input signal')

Compare circuit envelope and idealized baseband simulations and observe the simulation fidelity overlaps.

f2 = figure;
subplot(2,1,1),plot(real(outCE)),hold('on'),plot(real(outIdeal),'+')
legend(['CE - ' num2str(tocCE) ' seconds'],['Ideal - ' num2str(tocIdeal) ' seconds'])
title('Real')
subplot(2,1,2),plot(imag(outCE)),hold('on'),plot(imag(outIdeal),'+')
legend(['CE - ' num2str(tocCE) ' seconds'],['Ideal - ' num2str(tocIdeal) ' seconds'])
title('Imag')
sgtitle('Simulation fidelity between circuit envelope and idealized baseband simulation')

Observe the simulation fidelity between two solvers and their computation time. The data points overlap.

Compare Simulation Results to RF Budget Output

Release the rfsystem System object from fast restart.

release(rfsCE)
release(rfsIdeal)

Define the input signal to the system.

in_DC = 10^((in_dBm-30)/20)*((1+1j)/sqrt(2));

Observe that circuit envelope and idealized baseband simulations give similar output power.

outCE_DC = rfsCE(in_DC);
outIdeal_DC = rfsIdeal(in_DC);
outCE_DC_dBm = 20*log10(abs(outCE_DC)) + 30
outIdeal_DC_dBm = 20*log10(abs(outIdeal_DC)) + 30

outCE_DC_dBm =

   34.2893


outIdeal_DC_dBm =

   34.2893

Observe the output power computed from the rfbudget object.

Note that the mismatch loss calculations using the rfsystem and rfbudget objects are based on the computeBudget method, but output power calculations between these two objects differ because mismatch loss calculations employ rational interpolation to ensure causality and passivity for transient simulation, whereas rfbudget does not.

rfbudget_DC_dBm = rfobj.OutputPower(end)

rfbudget_DC_dBm =

   34.3116

Tips

  • Create multiple rfsystem outputs using this optional syntax:

    [out(1:n).val] = rfs(in)

    , where n is the number of output chains in a single-input multiple-output (SIMO) transmitter system 'Tx' using the input signal in.

Version History

Introduced in R2021a

expand all

See Also

| | |

Topics