setSolverMINLP
Choose mixed integer nonlinear programming (MINLP) solver for portfolio optimization
Description
obj = setSolverMINLP(obj,solverTypeMINLP)Portfolio, PortfolioCVaR, or PortfolioMAD object.
When any one or any combination of 'Conditional'
BoundType, MinNumAssets, or
MaxNumAssets constraints are active, the portfolio problem is formulated by
adding NumAssets binary variables. The binary variable 0
indicates that an asset is not invested and the binary variable 1 indicates
that an asset is invested. For more information on using 'Conditional'
BoundType, see setBounds. For more information
on specifying MinNumAssets and MaxNumAssets, see
setMinMaxNumAssets.
If you use the Financial Toolbox™
estimate functions with a Portfolio,
PortfolioCVaR, or PortfolioMAD object for which any of
the 'Conditional'
BoundType, MinNumAssets, or
MaxNumAssets constraints are active, MINLP solver is automatically used.
For details on MINLP, see Algorithms and Choose MINLP Solvers for Portfolio Problems.
obj = setSolverMINLP(___,Name,Value)
Examples
Configure the MINLP solver for a three-asset portfolio for which you have the mean and covariance values of the asset returns.
AssetMean = [ 0.0101110; 0.0043532; 0.0137058 ];
AssetCovar = [ 0.00324625 0.00022983 0.00420395;
0.00022983 0.00049937 0.00019247;
0.00420395 0.00019247 0.00764097 ];
p = Portfolio('AssetMean', AssetMean, 'AssetCovar', AssetCovar);When working with a Portfolio object, use setBounds with a 'Conditional'BoundType constraint to set xi = 0 or 0.02 <= xi <= 0.5 for all i = 1,...NumAssets.
p = setBounds(p, 0.02, 0.5,'BoundType', 'Conditional', 'NumAssets', 3);
When working with a Portfolio object, use setMinMaxNumAssets function to set up MinNumAssets and MaxNumAssets constraints for a portfolio. This sets limit constraints for the Portfolio object, where the total number of allocated assets satisfying the constraints is between MinNumAssets and MaxNumAssets. Setting MinNumAssets = MaxNumAssets = 2, specifies that only two of the three assets are invested in the portfolio.
p = setMinMaxNumAssets(p, 2, 2);
Three different MINLP solvers (OuterApproximation, ExtendedCP, TrustRegionCP) use the cutting plane method. Use the setSolverMINLP function to configure the OuterApproximation solver and options.
pint = setSolverMINLP(p,'OuterApproximation', 'NonlinearScalingFactor', 1e4, 'Display', 'iter', 'CutGeneration', 'basic'); pint.solverTypeMINLP
ans = 'OuterApproximation'
pint.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 10000
ObjectiveScalingFactor: 1000
Display: 'iter'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
You can also configure the options for intlinprog, which is the Main solver for mixed integer linear programming problems in the MINLP solver.
pint = setSolverMINLP(p,'OuterApproximation', 'IntMainSolverOptions', optimoptions('intlinprog','Display','off')); pint.solverOptionsMINLP.IntMainSolverOptions
ans =
intlinprog options:
Options used by current Algorithm ('highs'):
(Other available algorithms: 'legacy')
Set properties:
Display: 'off'
Default properties:
AbsoluteGapTolerance: 1.0000e-06
Algorithm: 'highs'
ConstraintTolerance: 1.0000e-06
MaxFeasiblePoints: 2.1475e+09
MaxNodes: 10000000
MaxTime: 7200
ObjectiveCutOff: Inf
OutputFcn: []
PlotFcn: []
RelativeGapTolerance: 1.0000e-04
Show options not used by current Algorithm ('highs')
Configure the MINLP solver for a 12 asset portfolio that is using semicontinuous and cardinality constraints.
load CAPMuniverse p = PortfolioCVaR('AssetList',Assets(1:12)); p = simulateNormalScenariosByData(p, Data(:,1:12),20000,'missingdata',true); p = setProbabilityLevel(p, 0.95);
When working with a PortfolioCVaR object, the setMinMaxNumAssets function enables you to set up the limits on the number of assets invested. The following example specifies that a minimum of five assets and a maximum of 10 assets should be invested using setMinMaxNumAssets and the investments should be greater than 4% and less than 45% using setBounds.
p = setMinMaxNumAssets(p, 5, 10); p = setBounds(p, 0.04, 0.45, 'BoundType','conditional');
Three different MINLP solvers (OuterApproximation, ExtendedCP, TrustRegionCP) use the cutting plane method. Use the setSolverMINLP function to configure the OuterApproximation solver and options.
pint = setSolverMINLP(p,'OuterApproximation','NonlinearScalingFactor', 1e4, 'Display', 'iter', 'CutGeneration', 'basic'); pint.solverTypeMINLP
ans = 'OuterApproximation'
pint.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 10000
ObjectiveScalingFactor: 1000
Display: 'iter'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
You can also configure the options for intlinprog, which is the Main solver for mixed integer linear programming problems in the MINLP solver.
pint = setSolverMINLP(p,'OuterApproximation','IntMainSolverOptions', optimoptions('intlinprog','Display','off')); pint.solverOptionsMINLP.IntMainSolverOptions
ans =
intlinprog options:
Options used by current Algorithm ('highs'):
(Other available algorithms: 'legacy')
Set properties:
Display: 'off'
Default properties:
AbsoluteGapTolerance: 1.0000e-06
Algorithm: 'highs'
ConstraintTolerance: 1.0000e-06
MaxFeasiblePoints: 2.1475e+09
MaxNodes: 10000000
MaxTime: 7200
ObjectiveCutOff: Inf
OutputFcn: []
PlotFcn: []
RelativeGapTolerance: 1.0000e-04
Show options not used by current Algorithm ('highs')
Configure the MINLP solver for a 12 asset portfolio that is using semicontinuous and cardinality constraints.
load CAPMuniverse p = PortfolioMAD('AssetList',Assets(1:12)); p = simulateNormalScenariosByData(p, Data(:,1:12), 20000 ,'missingdata',true);
When working with a PortfolioMAD object, the setMinMaxNumAssets function enables you to set up the limits on the number of assets invested. The following example specifies that a minimum of five assets and a maximum of 10 assets should be invested using setMinMaxNumAssets and the investments should be greater than 4% and less than 45% using setBounds.
p = setMinMaxNumAssets(p, 5, 10); p = setBounds(p, 0.04, 0.45, 'BoundType', 'conditional');
Three different MINLP solvers (OuterApproximation, ExtendedCP, TrustRegionCP) use the cutting plane method. Use the setSolverMINLP function to configure the OuterApproximation solver and options.
pint = setSolverMINLP(p,'OuterApproximation', 'NonlinearScalingFactor', 1e4, 'Display', 'iter', 'CutGeneration', 'basic'); pint.solverTypeMINLP
ans = 'OuterApproximation'
pint.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 10000
ObjectiveScalingFactor: 1000
Display: 'iter'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
You can also configure the options for intlinprog, which is the Main solver for mixed integer linear programming problems in the MINLP solver.
pint = setSolverMINLP(p,'OuterApproximation', 'IntMainSolverOptions', optimoptions('intlinprog','Display','off')); pint.solverOptionsMINLP.IntMainSolverOptions
ans =
intlinprog options:
Options used by current Algorithm ('highs'):
(Other available algorithms: 'legacy')
Set properties:
Display: 'off'
Default properties:
AbsoluteGapTolerance: 1.0000e-06
Algorithm: 'highs'
ConstraintTolerance: 1.0000e-06
MaxFeasiblePoints: 2.1475e+09
MaxNodes: 10000000
MaxTime: 7200
ObjectiveCutOff: Inf
OutputFcn: []
PlotFcn: []
RelativeGapTolerance: 1.0000e-04
Show options not used by current Algorithm ('highs')
This example shows how to solve a portfolio optimization problem with constraints in the number of selected assets and conditional (semi-continuous) bounds. This example demonstrates setSolverMINLP support for extended formulation, using the name-value argument ExtendedFormulation, for the OuterApproximation solverTypeMINLP. The extended formulation reformulates problems with quadratic functions to work in an extended space to decrease the computation time.
Create Mean-Variance Portfolio
Load the returns data in CAPMuniverse.mat. Then, create a standard mean-variance Portfolio object with default constraints, a long-only portfolio whose weights sum to 1. For this example, you can define the feasible region of weights as
% Load data load CAPMuniverse.mat % Create a mean-variance Portfolio object with default constraints p = Portfolio(AssetList=Assets(1:12)); p = estimateAssetMoments(p,Data(:,1:12)); p = setDefaultConstraints(p); p.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 1000
ObjectiveScalingFactor: 1000
Display: 'off'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
Include binary variables for this scenario by setting conditional (semicontinuous) bounds using setBounds. Conditional bounds are those such that or . In this example, for all assets.
% Set conditional bounds condLB = 0.1; condUB = 0.5; p = setBounds(p,condLB,condUB,BoundType="conditional")
p =
Portfolio with properties:
BuyCost: []
SellCost: []
RiskFreeRate: []
AssetMean: [12×1 double]
AssetCovar: [12×12 double]
TrackingError: []
TrackingPort: []
Turnover: []
BuyTurnover: []
SellTurnover: []
Name: []
NumAssets: 12
AssetList: {'AAPL' 'AMZN' 'CSCO' 'DELL' 'EBAY' 'GOOG' 'HPQ' 'IBM' 'INTC' 'MSFT' 'ORCL' 'YHOO'}
InitPort: []
AInequality: []
bInequality: []
AEquality: []
bEquality: []
LowerBound: [12×1 double]
UpperBound: [12×1 double]
LowerBudget: 1
UpperBudget: 1
GroupMatrix: []
LowerGroup: []
UpperGroup: []
GroupA: []
GroupB: []
LowerRatio: []
UpperRatio: []
MinNumAssets: []
MaxNumAssets: []
ConditionalBudgetThreshold: []
ConditionalUpperBudget: []
BoundType: [12×1 categorical]
Set ExtendedFormulation of OuterApproximation
Use setSolverMINLP to apply the extended formulation to the problem by setting the solverTypeMINLP argument for OuterApproximation and the ExtendedFormulation name-value argument to true. The extended formulation reformulates problems with quadratic functions to work in an extended space to decrease the computation time. You can use the name-value arguments NumInnerCuts and NumInitialOuterCuts to control the extended formulation algorithm:
NumInnerCuts— Number of cuts per asset added to the inner approximation problem to obtain an initial feasible point and upper boundNumInitialOuterCuts— Number of cuts per asset added to the initial outer approximation problem.
% Increase the number of inner cuts and initial outer cuts pEOA = setSolverMINLP(p,'OuterApproximation',ExtendedFormulation=true,NumInnerCuts=20,NumInitialOuterCuts=20); pEOA.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 1000
ObjectiveScalingFactor: 1000
Display: 'off'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 1
NumInnerCuts: 20
NumInitialOuterCuts: 20
Estimate Set of Portfolios on Efficient Frontier
Use estimateFrontier to compute the efficient frontier, which is the curve that shows the trade-off between the return and risk achieved by Pareto-optimal portfolios. For a given return level, the portfolio on the efficient frontier is the one that minimizes the risk while maintaining the desired return. Conversely, for a given risk level, the portfolio on the efficient frontier is the one that maximizes return while maintaining the desired risk level. Compute risks and returns of the portfolios on the efficient frontier.
% Find the efficient frontier
wEOA = estimateFrontier(pEOA)wEOA = 12×10
0 0 0.1000 0.1253 0.1745 0.2236 0.2715 0.3327 0.4111 0.5000
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0.1350 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0.1000 0.1450 0.1406 0.1910 0.2344 0.2778 0.3200 0.3726 0.4415 0.5000
0.1000 0.1609 0.1642 0.2121 0.2415 0.2709 0.3085 0.2947 0.1474 0
0.2354 0.1875 0.1290 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0.4296 0.4066 0.3662 0.3717 0.2496 0.1277 0 0 0 0
0 0.1000 0.1000 0.1000 0.1000 0.1000 0.1000 0 0 0
0 0 0 0 0 0 0 0 0 0
⋮
% Compute risk and returns of the portfolios on the efficient frontier
[rskEOA,retEOA] = estimatePortMoments(p,wEOA)rskEOA = 10×1
0.0076
0.0080
0.0085
0.0094
0.0105
0.0117
0.0132
0.0147
0.0168
0.0193
retEOA = 10×1
0.0008
0.0012
0.0017
0.0021
0.0026
0.0030
0.0034
0.0039
0.0043
0.0048
Maximize Return by Risk
Problems modeled to obtain the efficient frontier are of the type that minimizes risk subject to a return level. Another common portfolio problem is one that maximizes return for a fixed risk level. The risk level selected should be achievable by the portfolio. That is, the risk level should be between the risk attained by the minimum risk portfolio and the maximum return portfolio. The following code first checks if the target risk level is achievable and, if it is, computes the portfolio that maximizes the return subject to the target risk level.
% Set a risk level that is "achievable"
targetRisk_A = mean(rskEOA);
wAchievRisk = estimateFrontierByRisk(p,targetRisk_A)wAchievRisk = 12×1
0.2322
0.0000
0.0000
0.0000
0.0000
0.2853
0.2760
0.0000
0.0000
0.1065
0.1000
0.0000
⋮
Input Arguments
Object for portfolio, specified using Portfolio,
PortfolioCVaR, or PortfolioMAD object. For more
information on creating a portfolio object, see
Data Types: object
MINLP solver for portfolio optimization when any one or any combination of
'Conditional'
BoundType, MinNumAssets, or
MaxNumAssets constraints are active. Specify
solverTypeMINLP using a character vector or string with a value of
'OuterApproximation', or 'ExtendedCP',
'TrustRegionCP'.
Using Portfolio Object
For a
Portfolioobject, when using the default value of thesolverTypeMINLPas'OuterApproximation', the following name-value arguments, with their default values, are supported forsetSolverMINLP:MaxIterations—1000AbsoluteGapTolerance—1.0000e-07RelativeGapTolerance—1.0000e-05Display—'off'NonlinearScalingFactor—1000ObjectiveScalingFactor—1000ExtendedFormulation—falseCutGeneration—'basic'ActiveCutTolerance—1.0000e-07IntMainSolverOptions—optimoptions('intlinprog',’Algorithm’,’legacy’,'Display','off','ConstraintTolerance',1e-5,'MaxTime',1000,'IPPreprocess','none','CutGeneration','advanced','Heuristics','rins','IntegerTolerance',1e-5,'NodeSelection','mininfeas','LPPreprocess','none')
For the extended formulation with a
Portfolioobject, when you specify the value of thesolverTypeMINLPas'OuterApproximation'and set the name-value argumentExtendedFormulationtotrue, the following name-value arguments, with their default values, are supported forsetSolverMINLP:MaxIterations—1000AbsoluteGapTolerance—1.0000e-07RelativeGapTolerance—1.0000e-05Display—'off'NonlinearScalingFactor—1000ObjectiveScalingFactor—1000ExtendedFormulation—trueNumInnerCuts—10NumInitialOuterCuts—10MaxIterationsInactiveCut—30NumIterationsEarlyIntegerConvergence—30ActiveCutTolerance—1.0000e-07IntMainSolverOptions—optimoptions('intlinprog',’Algorithm’,’legacy’,'Display','off','ConstraintTolerance',1e-5,'MaxTime',1000,'IPPreprocess','none','CutGeneration','advanced','Heuristics','rins','IntegerTolerance',1e-5,'NodeSelection','mininfeas','LPPreprocess','none')
For more information on the extended formulation solver, see Extended Formulation. For examples of using extended formulation, see Use Extended Formulation of OuterApproximation Solver Type and Mixed-Integer Mean-Variance Portfolio Optimization Problem.
Using PortfolioCVaR or PortfolioMAD Object
For a PortfolioCVaR and PortfolioMAD object, the
default value of the solverTypeMINLP is 'TrustRegionCP'
with the following default settings for name-value pairs for setSolverMINLP:
MaxIterations—1000AbsoluteGapTolerance—1.0000e-07RelativeGapTolerance—1.0000e-05Display—'off'NonlinearScalingFactor—1000ObjectiveScalingFactor—1000CutGeneration—'basic'MaxIterationsInactiveCut—30NumIterationsEarlyIntegerConvergence—30ActiveCutTolerance—1.0000e-07ShrinkRatio—0.75InitialDelta—0.5DeltaLimit—1e6DeltaLowerBound—0.01IntMainSolverOptions—optimoptions('intlinprog',’Algorithm’,’legacy’,'Display','off','ConstraintTolerance',1e-5,'MaxTime',1000,'IPPreprocess','none','CutGeneration','advanced','Heuristics','rins','IntegerTolerance',1e-5,'NodeSelection','mininfeas','LPPreprocess','none')
Data Types: char | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: p =
setSolverMINLP(p,'ExtendedCP','MaxIterations',10000,'NonlinearScalingFactor',1000)
Maximum number of iterations, specified as the comma-separated pair consisting of
'MaxIterations' and a nonnegative integer value.
Data Types: double
Scaling factor for nonlinear function and gradient, specified as the comma-separated
pair consisting of 'NonlinearScalingFactor' and a nonnegative real
value.
Data Types: double
Scales the objective function used by the MainSolver by a factor, specified as the
comma-separated pair consisting of 'ObjectiveScalingFactor' and a
nonnegative real value.
Data Types: double
The solver stops if the absolute difference between the approximated nonlinear function
value and its true value is less than or equal to AbsoluteGapTolerance.
AbsoluteGapTolerance is specified as the comma-separated pair consisting
of 'AbsoluteGapTolerance' and a nonnegative real value.
Data Types: double
The solver stops if the relative difference between the approximated nonlinear function
value and its true value is less than or equal to RelativeGapTolerance.
RelativeGapTolerance is specified as the comma-separated pair consisting
of 'AbsoluteGapTolerance' and a nonnegative real value.
Data Types: double
Display output format, specified as the comma-separated pair consisting of
'Display' and a character vector with a value of:
'off'— Display no output'iter'— Display output at each iteration and the technical exit message'final'— Display only the final output and the final technical exit message
Data Types: char
Cut specification, specified as the comma-separated pair consisting of
'CutGeneration' and a character vector with one of these values:
'basic'— Add the new cut at the latest solution found.'midway'— Add the new cut at the midpoint between the latest and previous solutions found.
Data Types: char
Since R2023b
Extend problem if all functions are linear or quadratic for a
Portfolio object, specified as the comma-separated pair consisting of
'ExtendedFormulation' and a logical value:
true— If possible, use extended formulation. When set totrue, you can specify a value forNumInnerCutsandNumInitialOuterCuts.false— Use original formulation.
For more information on the extended formulation solver, see Extended Formulation. For an example of using extended formulation, see Use Extended Formulation of OuterApproximation Solver Type and Mixed-Integer Mean-Variance Portfolio Optimization Problem.
Data Types: logical
Since R2023b
Number of inner cuts (secant lines) added per asset to find a feasible point, specified
as the comma-separated pair consisting of 'NumInnerCuts' and a positive
numeric value ≤ 20. Consider decreasing NumInnerCuts
when the number of assets is greater than 100.
Note
NumInnerCuts is only applied when
ExtendedFormulation is set to true. If
NumInnerCuts = 0, the solver does not solve an inner
approximation to find an initial feasible point.
For more information on the extended formulation solver, see Extended Formulation. For an example of using extended formulation, see Use Extended Formulation of OuterApproximation Solver Type and Mixed-Integer Mean-Variance Portfolio Optimization Problem.
Data Types: double
Since R2023b
Number outer cuts added at the beginning of the algorithm to start the iterations with a
more accurate approximation, specified as the comma-separated pair consisting of
'NumInitialOuterCuts' and a positive numeric value ≤
20. Consider decreasing NumInitialOuterCuts when the
number of assets is greater than 100
Note
NumInitialOuterCuts is only applied when
ExtendedFormulation is set to true. If
NumInitialOuterCuts = 0, the initial MILP
approximation starts without outer cuts.
For more information on the extended formulation solver, see Extended Formulation. For an example of using extended formulation, see Use Extended Formulation of OuterApproximation Solver Type.
Data Types: double
Removes constraints that are not active for the last
MaxIterationsInactiveCut iterations, specified as the comma-separated
pair consisting of 'MaxIterationsInactiveCut' and a nonnegative integer
value. Generally, the MaxIterationsInactiveCut value is larger than
10.
Data Types: double
When the integer variable solution is stable for the last
NumIterationsEarlyIntegerConvergence iterations, the solver computes a
final NLP by using the latest integer variable solution in the MILP.
NumIterationsEarlyIntegerConvergence is specified as the comma-separated
pair consisting of 'NumIterationsEarlyIntegerConvergence' and a
nonnegative integer value.
Data Types: double
Determines if the cuts are active, specified as the comma-separated pair consisting of
'ActiveCutTolerance' and a nonnegative real value.
ActiveCutTolerance is used together with
MaxIterationsInactiveCut to decide which cuts to remove from the MILP
subproblem.
Data Types: double
Solver starts to apply the trust region heuristic at
TrustRegionStartIteration, specified as the comma-separated pair
consisting of 'TrustRegionStartIteration' and a nonnegative integer.
Note
The TrustRegionStartIteration name-value pair argument can only be
used with a solverTypeMINLP of
'TrustRegionCP'.
Data Types: double
Ratio to shrink size of trust region, specified as the comma-separated pair consisting
of 'ShrinkRatio' and a nonnegative real value between 0
and 1. If the approximated functions do not have good agreement in the
previous iterations, the algorithm uses this ratio to shrink the trust-region size.
Note
The ShrinkRatio name-value pair argument can only be used with a
solverTypeMINLP of 'TrustRegionCP'.
Data Types: double
Since R2022a
Value to initialize trust region, specified as the comma-separated pair consisting of
'InitialDelta' and a nonnegative real value.
Note
The InitialDelta name-value pair argument can only be used with a
solverTypeMINLP of 'TrustRegionCP'.
Data Types: double
Trust region of the approximated functions is bounded by DeltaLimit
during the iterations, specified as the comma-separated pair consisting of
'DeltaLimit' and a nonnegative real value.
Note
The DeltaLimit name-value pair argument can only be used with a
solverTypeMINLP of 'TrustRegionCP'.
Modifying 'DeltaLimit' might result in the solver not being able to
find a solution.
If you modify 'DeltaLimit' without specifying a value for
'InitialDelta', the 'InitialDelta' is
automatically set to InitialDelta' =
'DeltaLimit'/2.
Data Types: double
Since R2023a
Set lower bound for the trust-region radius, specified as the comma-separated pair
consisting of 'DeltaLowerBound' and a numeric value in
[0,1] that can include 0 and 1.
Note
The DeltaLowerBound name-value pair argument can only be used with
a solverTypeMINLP of 'TrustRegionCP'.
Data Types: double
Since R2023b
quadprog options to solve the continuous version of the mixed-integer
quadratic problem (MIQP), specified as the comma-separated pair consisting of
'QuadprogOptions' and an quadprog
optimoptions object.
Data Types: optim.options.Quadprog
Since R2023b
fmincon options to solve the continuous version of the mixed-integer
non-linear problem (MINLP), specified as the comma-separated pair consisting of
'FminconOptions' and a fmincon
optimoptions object.
Data Types: optim.options.Fmincon
Since R2023b
Nonnegative value subtracted from (when minimizing) or added to (when maximizing) the
objective bound to account for numerical inaccuracies in the objective bound, specified as
the comma-separated pair consisting of 'ObjectiveBoundRelaxation' and a
nonnegative numeric value.
Data Types: double
Since R2023b
Number of iterations allowed for the objective lower and upper bounds difference to
remain the same before stopping the algorithm, specified as the comma-separated pair
consisting of 'MaxIterationsGapStall' and an integer.
Data Types: double
Since R2023a
Options for the main solver intlinprog, specified as the comma-separated pair consisting of
'IntMainSolverOptions' and an optimoptions object.
Example: 'IntMainSolverOptions',
optimoptions('intlinprog','Display','off')
Data Types: object
Output Arguments
Updated portfolio object, returned as a Portfolio,
PortfolioCVaR, or PortfolioMAD object.
More About
All three MINLP solvers ('OuterApproximation',
'ExtendedCP', and 'TrustRegionCP') defined by
solverTypeMINLP rely on the cutting plane concept.
These MINLP solvers approximate the nonlinear convex function f(x) by a piecewise linear approximation, which is a sequence of linear cuts around the original function. In this way, the original MINLP is reduced to a sequence of MILP subproblems, each one with a more refined approximation to f(x) than previous MILPs, and yields a more optimal solution. The process continues until the solution found from MILP converges to the true function value within a certain tolerance.
The
'ExtendedCP'solver iteratively adds a linear cut at the latest solution found to approximate f(x).The
'OuterApproximation'solver is similar to'ExtendedCP', but they differ in where to add the cut. Instead of using the solution from the latest MILP,OuterApproximationuses the values of integer variables from the latest MILP solution and fixes them to reduce the MINLP to a nonlinear programming (NLP) problem. The cut is added at the solution from this NLP problem.The
'TrustRegionCP'solver is a version of'ExtendedCP'that is modified to speed up the optimization process. In general, the trust region method uses a model to approximate the true function within a region at each iteration. In the context of the MINLP solver, the model is the maximum of all the added cuts. The true function is the nonlinear function f(x) in the optimization problem. The region of the model is updated based on how well the model approximates the true function for the iteration. This approximation is the comparison of the predicted reduction of the objective function using the model vs. the true reduction.
The extended formulation solver can only be used
with a Portfolio object to solve problems to with quadratic functions, such
as variance and tracking error.
Assume the following problem
In the extended formulation, nonlinear functions must have separable terms, that is, each term must only depend on one variable. For example:
This allows the problem to be reformulated as
This reformulation obtains tighter approximations because, instead of adding just one cut
at each iteration, you are adding numVars cuts per iteration. Furthermore,
the univariate functions allow you to build a better initial approximation that helps to obtain
an initial feasible point. The initial approximation is achieved with the inner cuts. Unlike the
outer cuts that linearly approximate the nonlinear function with tangent lines, the inner cuts
use secant lines.
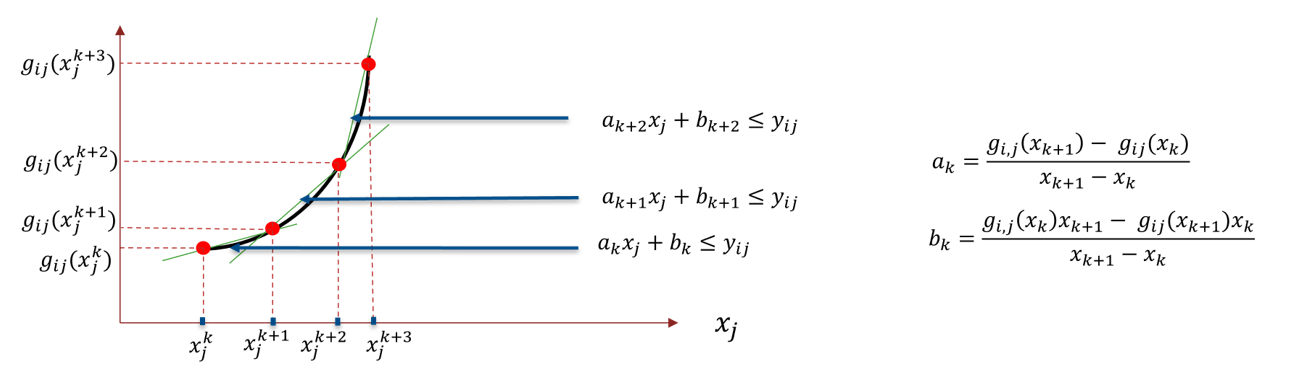
Quadratic functions are not originally separable. By introducing two sets of auxiliary variables (y and t), you can rewrite all quadratic functions in a problem as separable functions as long as the matrix of the quadratic coefficients is positive semidefinite.
Tips
You can also use dot notation to specify associated name-value options.
obj = obj.setSolverMINLP(Name,Value);
Note
The solverTypeMINLP and solverOptionsMINLP
properties cannot be set using dot notation because they are hidden properties. To set the
solverTypeMINLP and solverOptionsMINLP properties,
use the setSolverMINLP function directly.
Algorithms
When any one, or any combination of
'Conditional'
BoundType, MinNumAssets, or MaxNumAssets
constraints is active, the portfolio problem is formulated by adding NumAssets
binary variables. The binary variable 0 indicates that an asset is not
invested and the binary variable 1 indicates that an asset is invested.
The MinNumAssets and MaxNumAssets constraints narrow
down the number of active positions in a portfolio to the range of [minN,
maxN]. In addition, the 'Conditional'
BoundType constraint is to set a lower and upper bound so that the position is
either 0 or lies in the range [minWgt,
maxWgt]. These two types of constraints are incorporated into the portfolio
optimization model by introducing n variables,
νi, which only take binary values
0 and 1 to indicate whether the corresponding asset is
invested (1) or not invested (0). Here n
is the total number of assets and the constraints can be formulated as the following linear
inequality constraints:
In this equation, minN and maxN are
representations for MinNumAsset and MaxNumAsset that are
set using setMinMaxNumAssets. Also,
minWgt and maxWgt are representations for
LowerBound and UpperBound that are set using setBounds.
The portfolio optimization problem to minimize the variance of the portfolio, subject to achieving a target expected return and some additional linear constraints on the portfolio weights, is formulated as
In this equation, H represents the covariance and m represents the asset returns.
The portfolio optimization problem to maximize the return, subject to an upper limit on the variance of the portfolio return and some additional linear constraints on the portfolio weights, is formulated as
When the 'Conditional'
BoundType, MinNumAssets, and
MaxNumAssets constraints are added to the two optimization problems, the
problems become:
References
[1] Bonami, P., Kilinc, M., and J. Linderoth. "Algorithms and Software for Convex Mixed Integer Nonlinear Programs." Technical Report #1664. Computer Sciences Department, University of Wisconsin-Madison, 2009.
[2] Kelley, J. E. "The Cutting-Plane Method for Solving Convex Programs." Journal of the Society for Industrial and Applied Mathematics. Vol. 8, Number 4, 1960, pp. 703–712.
[3] Linderoth, J. and S. Wright. "Decomposition Algorithms for Stochastic Programming on a Computational Grid." Computational Optimization and Applications. Vol. 24, Issue 2–3, 2003, pp. 207–250.
[4] Nocedal, J., and S. Wright. Numerical Optimization. New York: Springer-Verlag, 1999.
Version History
Introduced in R2018bThe default for the name-value argument IntMainSolverOptions is
changed to
optimoptions('intlinprog',’Algorithm’,’legacy’,'Display','off','ConstraintTolerance',1e-5,'MaxTime',1000,'IPPreprocess','none','CutGeneration','advanced','Heuristics','rins','IntegerTolerance',1e-5,'NodeSelection','mininfeas','LPPreprocess','none').
To use the extended formulation solver with setSolverMINLP for a Portfolio object, you set the
solverTypeMINLP argument to OuterApproximation and
specify the name-value arguments for ExtendedFormulation,
NumInnerCuts, and NumInitialOuterCuts.
When using a Portfolio, PortfolioCVaR, or PortfolioMAD object, you can use the
setSolverMINLP name-value arguments for
QuadprogOptions, FminconOptions,
ObjectiveBoundRelaxation, and
MaxIterationsGapStall.
When using a solverTypeMINLP of 'TrustRegionCP',
you can use the 'DeltaLowerBound' name-value argument to set the lower
bound for the trust-region radius.
The 'IntMasterSolverOptions' name-value
argument is renamed to 'IntMainSolverOptions'. The use of
'IntMasterSolverOptions' name-value argument is
discouraged.
See Also
optimoptions | setBounds | setMinMaxNumAssets | estimateFrontier | estimateFrontierByReturn | estimateFrontierByRisk | estimateFrontierLimits | estimateMaxSharpeRatio | setSolver
Topics
- Portfolio Optimization with Semicontinuous and Cardinality Constraints
- Mixed-Integer Quadratic Programming Portfolio Optimization: Problem-Based
- Mixed-Integer CVaR Portfolio Optimization Problem
- Mixed-Integer MAD Portfolio Optimization Problem
- Mixed-Integer Mean-Variance Portfolio Optimization Problem
- Supported Constraints for Portfolio Optimization Using Portfolio Objects
- Supported Constraints for Portfolio Optimization Using PortfolioCVaR Object
- Supported Constraints for Portfolio Optimization Using PortfolioMAD Object
- Solver Guidelines for Portfolio Objects
- Choosing and Controlling the Solver for Mean-Variance Portfolio Optimization
- Choosing and Controlling the Solver for PortfolioCVaR Optimizations
- Choosing and Controlling the Solver for PortfolioMAD Optimizations
- Choose MINLP Solvers for Portfolio Problems
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)