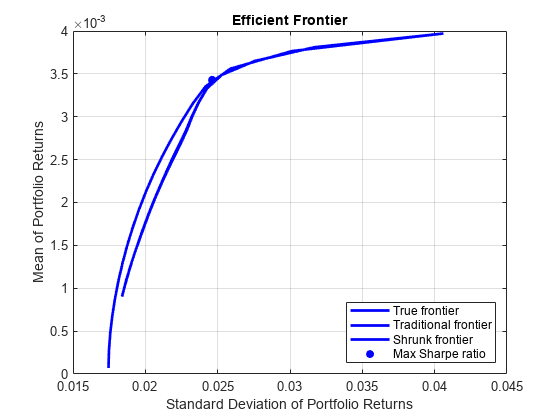
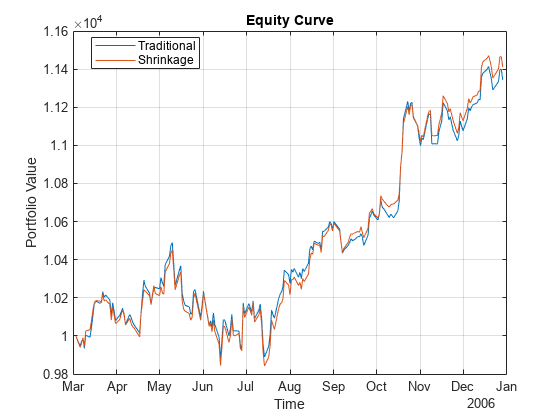
covarianceShrinkage
Description
SigmaHat = covarianceShrinkage(AssetReturns)
covarianceShrinkage computes an estimate of the covariance
matrix from a sample of asset returns using the multiple of the identity shrinkage
estimation method. For more information, see Covariance Shrinkage and covarianceShrinkage Algorithm.
In addition, you can use covarianceDenoising to compute an estimate of covariance matrix
using denoising. For information on which covariance estimation method to choose,
see Comparison of Methods for Covariance Estimation.
Examples
Input Arguments
Output Arguments
More About
Algorithms
The covarianceShrikage function applies a linear shrinkage method
that shrinks the traditional covariance estimate to a multiple of the identity matrix.
Here, Σ is the standard covariance estimate, τ is the average sample variance, and is the intensity parameter computed using
where zi is the i th row of the centered sample matrix Z and N is the sample size.
References
[1] Ledoit, O. and Wollf, M. "A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices." Journal of Multivariate Analysis. vol. 88, no. 2, 365–411, 2004.
Version History
Introduced in R2023a