Estimate Multiplicative ARIMA Model Using Econometric Modeler App
This example uses the Box-Jenkins method [1] to determine a multiplicative seasonal ARIMA (SARIMA) model for a univariate series by using the Econometric Modeler app. Specifically, the example shows this procedure:
Visually determine whether the series has an exponential trend, and then remove the trend if one is present.
The remaining steps determine the structure of the conditional mean model to fit to the series without the exponential trend.
Visually determine whether the transformed series has seasonal integration, and then remove the seasonal integration, if it is present, by taking the seasonal difference. Record the degrees of seasonal integration removed.
Determine whether the transformed series has a unit root by conducting a statistical test, and then apply the first difference to the series to stabilize it, if a unit root is present. Record whether a unit root exists.
Determine the nonseasonal AR and MA degrees of the conditional mean model for the stationary series by inspecting correlograms of the stabilized series. Record the polynomial degrees.
Use the results of steps 2 through 4 to create and estimate a conditional mean model for the nonstationary series with the exponential trend removed.
The data set Data_Airline.mat contains monthly counts of airline passengers.
Import Data into Econometric Modeler
At the command line, load the Data_Airline.mat data set.
load Data_AirlineAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variable PSSG appears in the Time
Series pane, its value appears in the
Preview pane, and its time series plot appears in the
Time Series Plot(PSSG) figure window.

The series exhibits a seasonal trend, serial correlation, and possible exponential growth. For an interactive analysis of serial correlation, see Detect Serial Correlation Using Econometric Modeler App.
Stabilize Series
To properly determine the lag operator polynomial orders for the conditional mean model, correlograms require a stationary series.
Address the exponential trend by applying the log transform to
PSSG.
In the Time Series pane, select
PSSG.On the Econometric Modeler tab, in the Transforms section, click Log.
The transformed variable PSSGLog
appears in the Time Series pane, its value appears in the
Preview pane, and its time series plot appears in the
Time Series Plot(PSSGLog) figure window.

The exponential growth appears to be removed from the series.
The rest of the example determines the parameters of conditional mean model
for the series PSSGLog by several visual and
statistical diagnoses and transformations.
Address the seasonal trend by applying the 12th order seasonal difference.
With PSSGLog selected in the Time
Series pane, on the Econometric Modeler tab,
in the Transforms section, set
Seasonal to 12. Then, click
Seasonal.
The transformed variable PSSGLogSeasonalDiff
appears in the Time Series pane, and its time series plot
appears in the Time Series Plot(PSSGLogSeasonalDiff) figure
window.
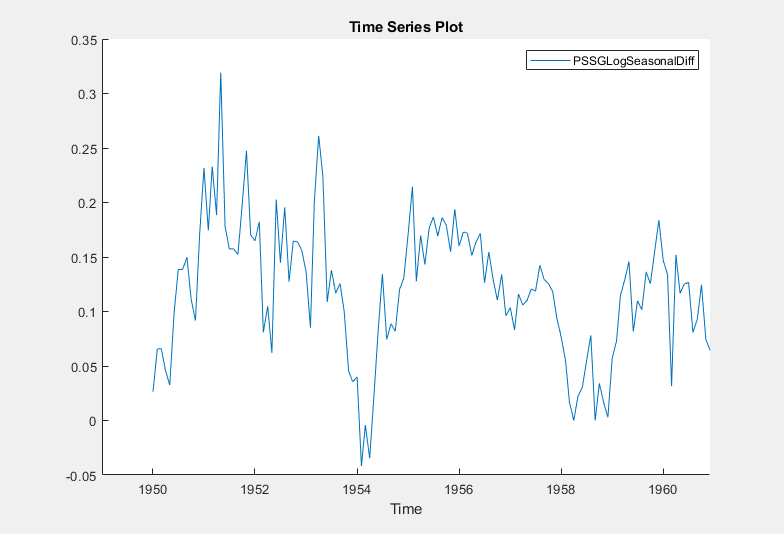
The transformed series appears to have a unit root.
Test the null hypothesis that PSSGLogSeasonalDiff
has a unit root by using the Augmented Dickey-Fuller test. Specify that the
alternative is an AR(0) model, then test again specifying an AR(1) model. Adjust
the significance level to 0.025 to maintain a total significance level of 0.05.
With
PSSGLogSeasonalDiffselected in the Time Series pane, on the Econometric Modeler tab, in the Tests section, click New Test > Augmented Dickey-Fuller Test.On the ADF tab, in the Parameters section, set Significance Level to
0.025.In the Tests section, click Run Test.
In the Parameters section, set Number of Lags to
1.In the Tests section, click Run Test.
The test results appear in the Results table of the ADF(PSSGLogSeasonalDiff) document.

Both tests fail to reject the null hypothesis that the series is a unit root process.
Address the unit root by applying the first difference to
PSSGLogSeasonalDiff. With
PSSGLogSeasonalDiff selected in the
Time Series pane, click the Econometric
Modeler tab. Then, in the Transforms
section, click Difference.
The transformed variable PSSGLogSeasonalDiffDiff
appears in the Time Series pane, and its time series plot
appears in the Time Series Plot(PSSGLogSeasonalDiffDiff)
figure window.
In the Time Series pane, rename the
PSSGLogSeasonalDiffDiff variable by clicking it
twice to select its name and entering
PSSGStable.
The app updates the names of all documents associated with the transformed series.

Identify Model for Series
Determine the lag structure for a conditional mean model of the series by plotting the sample autocorrelation function (ACF) and partial autocorrelation function (PACF) of the stabilized series.
With
PSSGStableselected in the Time Series pane, click the Plots tab, then click ACF.Show the first 50 lags of the ACF. On the ACF tab, set Number of Lags to
50.Click the Plots tab, then click PACF.
Show the first 50 lags of the PACF. On the PACF tab, set Number of Lags to
50.Drag the ACF(PSSGStable) figure window above the PACF(PSSGStable) figure window.
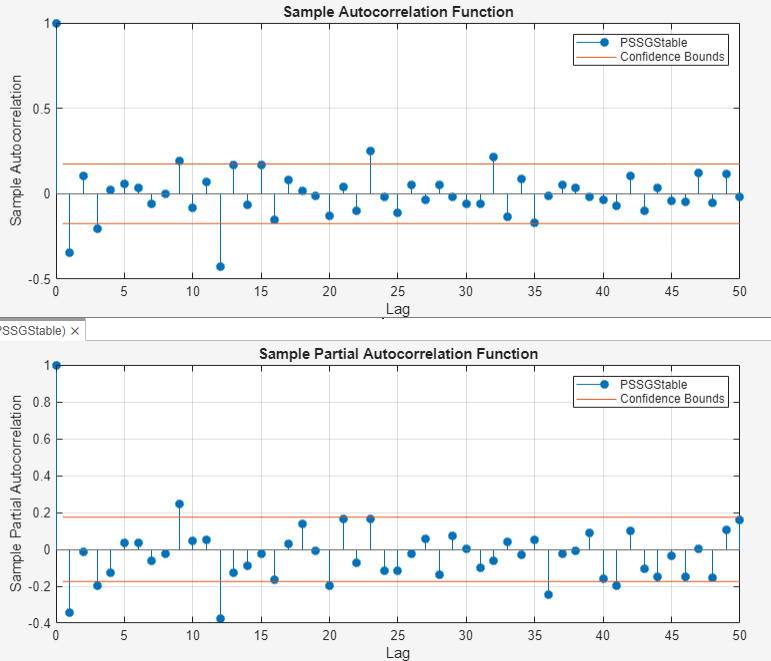
According to [1], the
autocorrelations in the ACF and PACF, the results in previous steps, and the
balance of model parsimony with complexity, suggest that the following
SARIMA(0,1,1)×(0,1,1)12 model is appropriate for the
nonstationary series with the exponential trend removed
PSSGLog.
Close all figure windows.
Specify and Estimate SARIMA Model
Specify the SARIMA(0,1,1)×(0,1,1)12 model.
In the Time Series pane, select the
PSSGLogtime series.On the Econometric Modeler tab, in the Models section, click the arrow > SARIMA.
In the SARIMA Model Parameters dialog box, on the Lag Order tab:
Nonseasonal section
Set Degrees of Integration to
1.Set Moving Average Order to
1.Clear the Include Constant Term check box.
Seasonal section
Set Period to
12to indicate monthly data.Set Moving Average Order to
1.Select the Include Seasonal Difference check box.

Click Estimate.
The model variable SARIMA_PSSGLog appears in the
Models pane, its value appears in the
Preview pane, and its estimation summary appears in the
Model Summary(SARIMA_PSSGLog) document.

The results include:
Model Fit — A time series plot of
PSSGLogand the fitted values fromSARIMA_PSSGLog.Residual Plot — A time series plot of the residuals of
SARIMA_PSSGLog.Parameters — A table of estimated parameters of
SARIMA_PSSGLog. Because the constant term was held fixed to 0 during estimation, its value and standard error are 0.Goodness of Fit — The AIC and BIC fit statistics of
SARIMA_PSSGLog.
References
[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.