Create Multiplicative Seasonal ARIMA Model for Time Series Data
This example shows how to specify a seasonal ARIMA model using arima. The time series is monthly international airline passenger numbers from 1949 to 1960.
Load the airline passenger data.
Load the airline data set, and then plot the natural log of the monthly passenger totals.
load Data_Airline y = log(DataTimeTable.PSSG); T = length(y); figure plot(DataTimeTable.Time,y) title("Log Airline Passengers")
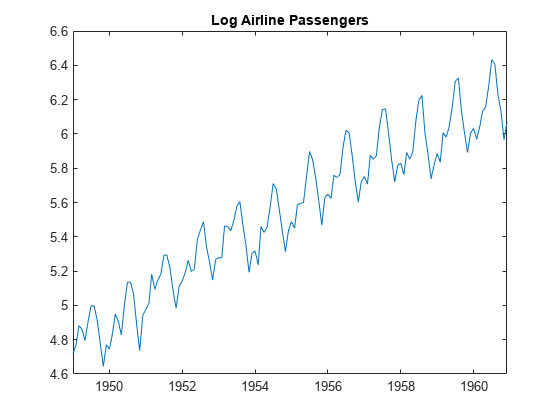
The series appears nonstationary, with a linear trend and seasonal periodicity.
Plot the seasonally integrated series.
Calculate the differenced series, , where is the original log-transformed data. Plot the differenced series.
A1 = LagOp({1,-1},Lags=[0 1]);
A12 = LagOp({1,-1},Lags=[0 12]);
dY = filter(A1*A12,y);
dT = T - length(dY);
figure
plot(DataTimeTable.Time((dT+1):T),dY)
title("Differenced Log Airline Passengers")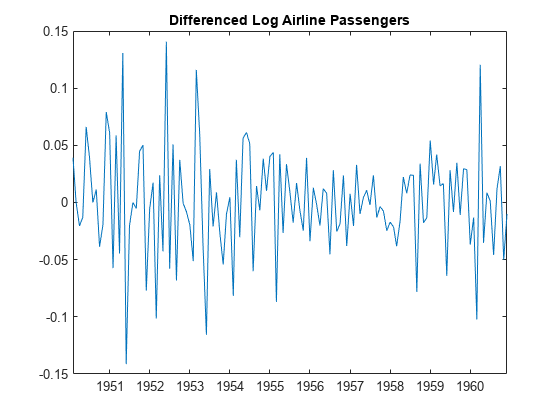
The differenced series appears stationary.
Plot the sample autocorrelation function (ACF).
figure autocorr(dY,NumLags=50)
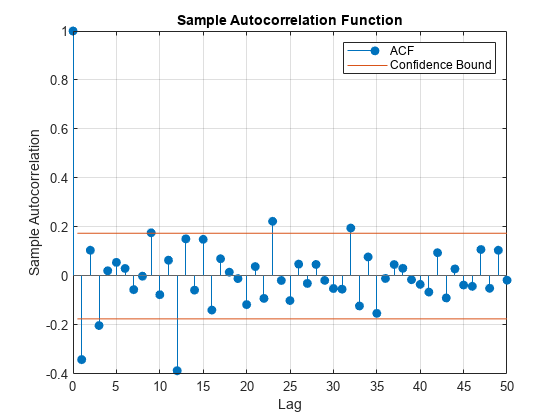
The sample ACF of the differenced series shows significant autocorrelation at lags that are multiples of 12. There is also potentially significant autocorrelation at smaller lags.
Specify a seasonal ARIMA model.
Box, Jenkins, and Reinsel suggest the multiplicative seasonal model,
for this data set [1].
Specify this model.
Mdl = arima(Constant=0,D=1,Seasonality=12, ...
MALags=1,SMALags=12)Mdl =
arima with properties:
Description: "ARIMA(0,1,1) Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 13
D: 1
Q: 13
Constant: 0
AR: {}
SAR: {}
MA: {NaN} at lag [1]
SMA: {NaN} at lag [12]
Seasonality: 12
Beta: [1×0]
Variance: NaN
The property P is equal to 13, corresponding to the sum of the nonseasonal and seasonal differencing degrees (1 + 12). The property Q is also equal to 13, corresponding to the sum of the degrees of the nonseasonal and seasonal MA polynomials (1 + 12). Parameters that need to be estimated have value NaN.
References
[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.