Autocorrelation and Partial Autocorrelation

What Are Autocorrelation and Partial Autocorrelation?

Autocorrelation is the linear dependence of a variable with itself at two points in time. For stationary processes, autocorrelation between any two observations depends only on the time lag h between them. Define Cov(y_t, y_t–h) = γ_h. Lag-h autocorrelation is given by

$${\rho }_h=Corr(y_t,y_{t-h})=\frac{{\gamma }_h}{{\gamma }_0}.$$

The denominator γ₀ is the lag 0 covariance, that is, the unconditional variance of the process.

Correlation between two variables can result from a mutual linear dependence on other variables (confounding). Partial autocorrelation is the autocorrelation between y_t and y_t–h after the removal of any linear dependence on y₁, y₂, ..., y_t–h+1. The partial lag-h autocorrelation is denoted $${\varphi }_{h,h}.$$

Theoretical ACF and PACF

The autocorrelation function (ACF) for a time series y_t, t = 1,...,N, is the sequence $${\rho }_h,$$ h = 1, 2,...,N – 1. The partial autocorrelation function (PACF) is the sequence $${\varphi }_{h,h},$$ h = 1, 2,...,N – 1.

The theoretical ACF and PACF for the AR, MA, and ARMA conditional mean models are known, and are different for each model. These differences among models are important to keep in mind when you select models.

Conditional Mean Model	ACF Behavior	PACF Behavior
AR(p)	Tails off gradually	Cuts off after p lags
MA(q)	Cuts off after q lags	Tails off gradually
ARMA(p,q)	Tails off gradually	Tails off gradually

Sample ACF and PACF

Sample autocorrelation and sample partial autocorrelation are statistics that estimate the theoretical autocorrelation and partial autocorrelation. Using these qualitative model selection tools, you can compare the sample ACF and PACF of your data against known theoretical autocorrelation functions [1].

For an observed series y₁, y₂,...,y_T, denote the sample mean $$\overline{y}.$$ The sample lag-h autocorrelation is given by

$${\widehat{\rho }}_h=\frac{{\displaystyle {\sum }_{t=h+1}^T(y_t-\overline{y})(y_{t-h}-\overline{y})}}{{\displaystyle {\sum }_{t=1}^T{(y_t-\overline{y})}^2}}.$$

The standard error for testing the significance of a single lag-h autocorrelation, $${\widehat{\rho }}_h$$, is approximately

$$S{E}_{\rho }=\sqrt{(1+2{\displaystyle {\sum }_{i=1}^{h-1}{\widehat{\rho }}_i^2})/N}.$$

When you use autocorr to plot the sample autocorrelation function (also known as the correlogram), approximate 95% confidence intervals are drawn at $$\pm 2SE\rho$$ by default. Optional input arguments let you modify the calculation of the confidence bounds.

The sample lag-h partial autocorrelation is the estimated lag-h coefficient in an AR model containing h lags, $${\widehat{\varphi }}_{h,h}.$$ The standard error for testing the significance of a single lag-h partial autocorrelation is approximately $$1/\sqrt{N}.$$ When you use parcorr to plot the sample partial autocorrelation function, approximate 95% confidence intervals are drawn at $$\pm 2/\sqrt{N}$$ by default. Optional input arguments let you modify the calculation of the confidence bounds.

Compute Sample ACF and PACF in MATLAB®

This example shows how to compute and plot the sample ACF and PACF of a time series by using the Econometrics Toolbox™ functions autocorr and parcorr, and the Econometric Modeler app.

Generate Synthetic Time Series

Simulate an MA(2) process ${\mathit{y}}_{\mathit{t}}$ by filtering a series of 1000 standard Gaussian deviates ${\epsilon }_{\mathit{t}}$through the difference equation

$$y_t={\epsilon }_t-{\epsilon }_{t-1}+{\epsilon }_{t-2}.$$

rng('default') % For reproducibility
e = randn(1000,1);
y = filter([1 -1 1],1,e);

Plot and Compute ACF

Plot the sample ACF of ${\mathit{y}}_{\mathit{t}}$ by passing the simulated time series to autocorr.

autocorr(y)

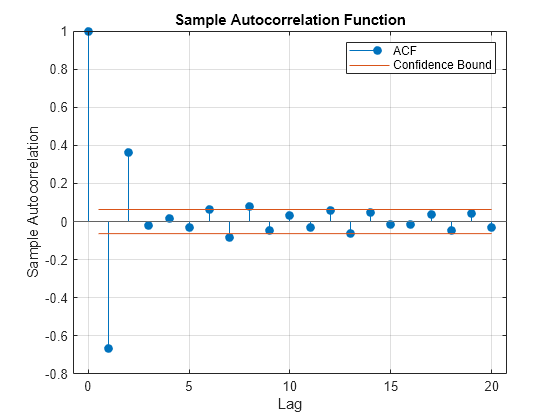
The sample autocorrelation of lags greater than 2 is insignificant.

Compute the sample ACF by calling autocorr again. Return the first output argument.

acf = autocorr(y)

acf = 21×1

    1.0000
   -0.6682
    0.3618
   -0.0208
    0.0146
   -0.0311
    0.0611
   -0.0828
    0.0772
   -0.0493
      ⋮

acf(j) is the sample autocorrelation of ${\mathit{y}}_{\mathit{t}}$ at lag j – 1.

Plot and Compute PACF

Plot the sample PACF of ${\mathit{y}}_{\mathit{t}}$ by passing the simulated time series to parcorr.

parcorr(y)

The sample PACF gradually decreases with increasing lag.

Compute the sample PACF by calling parcorr again. Return the first output argument.

pacf = parcorr(y)

pacf = 21×1

    1.0000
   -0.6697
   -0.1541
    0.2929
    0.3421
    0.0314
   -0.1483
   -0.2290
   -0.0394
    0.1419
      ⋮

pacf(j) is the sample partial autocorrelation of ${\mathit{y}}_{\mathit{t}}$ at lag j – 1.

The sample ACF and PACF suggest that ${\mathit{y}}_{\mathit{t}}$ is an MA(2) process.

Use Econometric Modeler

Open the Econometric Modeler app by entering econometricModeler at the command prompt.

econometricModeler

Load the simulated time series y.

1. On the Econometric Modeler tab, in the Import section, select Import > Import From Workspace.

2. In the Import Data dialog box, in the Import? column, select the check box for the y variable.

3. Click Import.

The variable y1 appears in the Data Browser, and its time series plot appears in the Time Series Plot(y1) figure window.

Plot the sample ACF by clicking ACF on the Plots tab.

Plot the sample PACF by clicking PACF on the Plots tab. Position the PACF plot below the ACF plot by dragging the PACF(y1) tab to the lower half of the document.

References

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.