armairf
Generate or plot ARMA model impulse responses
Syntax
Description
The armairf function returns or plots the impulse response functions (IRFs) of the variables in a univariate or vector (multivariate) autoregressive moving average (ARMA) model specified by arrays of coefficients or lag operator polynomials.
Alternatively, you can return an IRF from a fully specified (for example, estimated) model object by using the function in this table.
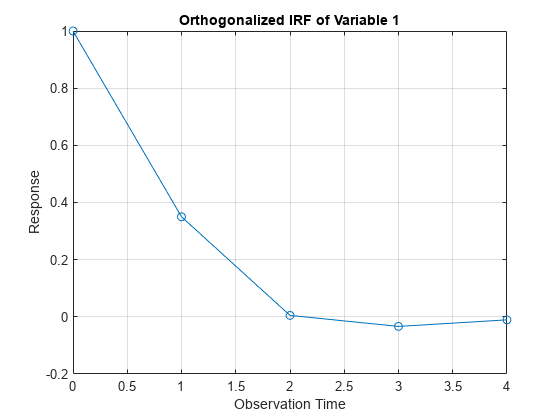
IRFs trace the effects of an innovation shock to one variable on the response of all variables in the system. In contrast, the forecast error variance decomposition (FEVD) provides information about the relative importance of each innovation in affecting all variables in the system. To estimate FEVDs of univariate or multivariate ARMA models, see armafevd.
armairf(
plots, in separate figures, the impulse response function of the time series
variables that compose an ARMA(p,q) model
with input autoregressive (AR) and moving average (MA) coefficients. Each figure
contains line plots over the forecast horizon, representing the responses of all
variables in the system to a one-standard-deviation shock, applied at time 0, to
one variable.ar0,ma0)
The armairf function:
Accepts vectors or cell vectors of matrices in difference-equation notation
Accepts
LagOplag operator polynomials corresponding to the AR and MA polynomials in lag operator notationAccommodates time series models that are univariate or multivariate, stationary or integrated, structural or in reduced form, and invertible or noninvertible
Assumes that the model constant c is 0
armairf(
plots the ar0,ma0,Name=Value)numVars IRFs with additional options specified by
one or more name-value arguments. For example,
NumObs=10,Method="generalized" specifies a 10-period
forecast horizon and the estimation of the generalized IRF.
armairf(
plots to the axes specified in ax,___)ax instead of
the axes in new figures. The option ax can precede any of the input argument
combinations in the previous syntaxes.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
To compute forecast error impulse responses, use the default value of
InnovCov, which is anumVars-by-numVarsidentity matrix. In this case, all available computation methods (seeMethod) result in equivalent IRFs.To accommodate structural ARMA(p,q) models, supply
LagOplag operator polynomials for the input argumentsar0andma0. To specify a structural coefficient when you callLagOp, set the corresponding lag to 0 by using theLagsname-value argument.For multivariate orthogonalized IRFs, arrange the variables according to Wold causal ordering [2]:
The first variable (corresponding to the first row and column of both
ar0andma0) is most likely to have an immediate impact (t = 0) on all other variables.The second variable (corresponding to the second row and column of both
ar0andma0) is most likely to have an immediate impact on the remaining variables, but not the first variable.In general, variable j (corresponding to row j and column j of both
ar0andma0) is the most likely to have an immediate impact on the lastnumVars– j variables, but not the previous j – 1 variables.
Algorithms
If
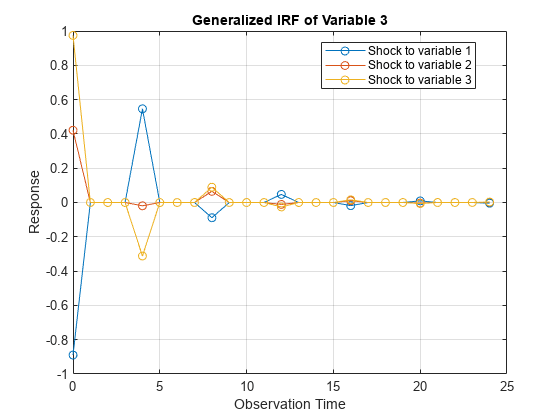
Methodis"orthogonalized", then the resulting IRF depends on the order of the variables in the time series model. IfMethodis"generalized", then the resulting IRF is invariant to the order of the variables. Therefore, the two methods generally produce different results.If
InnovCovis a diagonal matrix, then the resulting generalized and orthogonal IRFs are identical. Otherwise, the resulting generalized and orthogonal IRFs are identical only when the first variable shocks all variables (that is, all else being the same, both methods yield the sameY(:,1,:)).
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Lütkepohl, Helmut. New Introduction to Multiple Time Series Analysis. New York, NY: Springer-Verlag, 2007.
[3] Pesaran, H. H., and Y. Shin. "Generalized Impulse Response Analysis in Linear Multivariate Models." Economic Letters. Vol. 58, 1998, pp. 17–29.