dsphdl.IFFT
Compute inverse fast Fourier transform (IFFT)
Description
The dsphdl.IFFT
System object™ provides two architectures that implement the algorithm for FPGA and ASIC
applications. You can select an architecture that optimizes for either throughput or area.
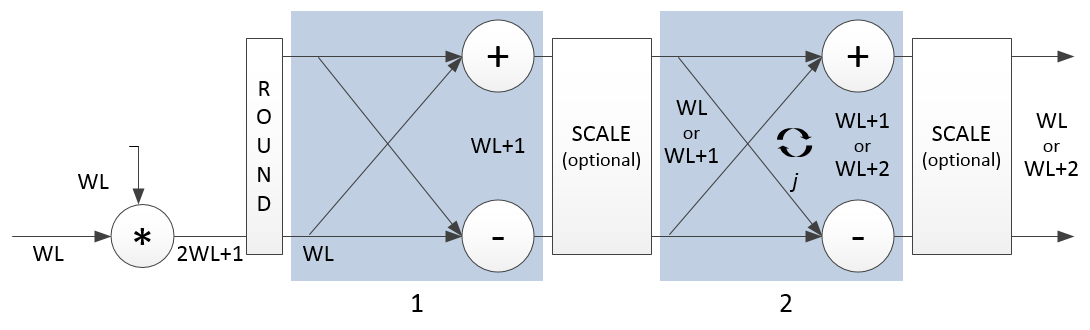
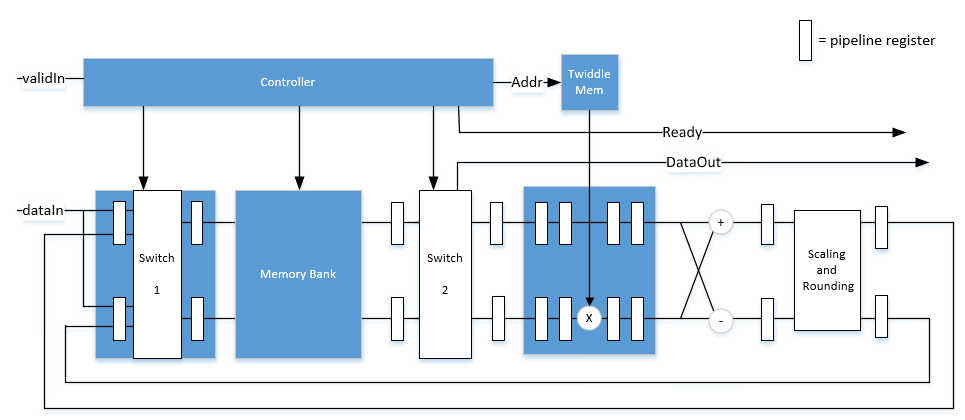
'Streaming Radix 2^2'— Use this architecture for high-throughput applications. This architecture supports scalar or vector input data. You can achieve gigasamples-per-second (GSPS) throughput, also called super sample rates, using vector input. Since 2025a, this architecture also supports specifying the FFT size by using an input port, when you use scalar input data.'Burst Radix 2'— Use this architecture for a minimum resource implementation, especially with large fast-Fourier-transform (FFT) sizes. Your system must be able to tolerate bursty data and higher latency. This architecture supports only scalar input data.
The object accepts real or complex data, provides hardware-friendly control signals, and has optional output frame control signals.
To calculate the inverse fast Fourier transform:
Create the
dsphdl.IFFTobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Note
You can also generate HDL code for this hardware-optimized algorithm, without creating a MATLAB® script, by using the DSP HDL IP Designer app. The app provides the same interface and configuration options as the System object.
Creation
Description
IFFT_N = dsphdl.IFFTIFFT_N, that performs a fast Fourier transform.
IFFT_N = dsphdl.IFFT(Name=Value)
Example: ifft128 = dsphdl.IFFT(FFTLength=128)
Properties
Usage
Syntax
Description
[
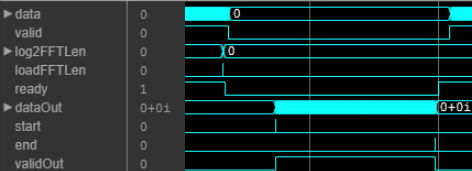
returns the next element of the IFFT when using the burst Radix 2
architecture. The Y,validOut,ready]
= IFFT_N(X,validIn)ready signal indicates when the object has memory
available to accept new input samples. When you use the burst architecture, you must send input data only when the ready backpressure signal is
1 (true). The object ignores any input data and
valid signals when ready is
0 (false).
To use this syntax, set the Architecture property to 'Burst Radix 2'. For example:
IFFT_N = dsphdl.IFFT(___,Architecture='Burst Radix 2'); ... [y,validOut,ready] = IFFT_N(x,validIn)
[
returns the next element of the IFFT when configured for a variable size FFT. Specify the
Y,validOut,ready]
= IFFT_var(X,validIn,log2FFTLen,loadFFTLen)log2FFTLen input argument as
log2(FFTLength). Set the
loadFFTLen input argument to 1
(true) to capture the value from the input
log2FFTLen argument.
When you use variable FFT length, you must send input data only when the
ready backpressure signal is 1
(true). The object sets the ready output
argument to 0 (false) if a new FFT length is
supplied while processing a frame of data. The object sets the ready
output argument to 1 (true) when it has completed a
frame of output data and has updated the FFT length for the next input frame.
To use this syntax, set the FFTLengthSource property to
'Input port'. For example:
IFFT_var = dsphdl.IFFT(___,Architecture='Streaming Radix 2^2', ... FFTLengthSource='Input port', ... FFTLengthMax=512); ... [y,validOut,ready] = IFFT_var(x,validIn,log2FFTLen,1) [y,validOut,ready] = IFFT_var(x,validIn,log2FFTLen,0)
[
also returns frame control signals Y,startOut,endOut,validOut]
= IFFT_N(X,validIn)startOut and
endOut. startOut is 1 (true) with
the first sample of a frame of output data. endOut is
1 (true) with the last sample of a frame of output data.
To use this syntax, set the StartOutputPort and EndOutputPort properties to true. For example:
IFFT_N = dsphdl.IFFT(___,StartOutputPort=true,EndOutputPort=true);
...
[y,startOut,endOut,validOut] = IFFT_N(x,validIn)[
returns the IFFT, Y,validOut]
= IFFT_N(X,validIn,resetIn)Y, when validIn is
1 (true) and resetIn is 0
(false).
When resetIn is 1 (true), the object stops the current
calculation and clears all internal state.
To use this syntax, set the ResetInputPort property to true. For example:
IFFT_N = dsphdl.IFFT(___,ResetInputPort=true);
...
[y,validOut] = IFFT_N(x,validIn,resetIn)Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)