Main Content

msesim

Estimated mean squared error for adaptive filters

collapse all in page

Syntax

mse = msesim(adaptFilt,x,d)
[mse,meanw,w,tracek] = msesim(adaptFilt,x,d)
[___] = msesim(adaptFilt,x,m)

Description

example

mse = msesim(adaptFilt,x,d) estimates the mean squared error of the adaptive filter at each time instant given the input and the desired response signal sequences in x and d.

example

[mse,meanw,w,tracek] = msesim(adaptFilt,x,d) also calculates the sequences of coefficient vector means, meanw, adaptive filter coefficients, w, and the total coefficient error powers, tracek, corresponding to the simulated behavior of the adaptive filter.

example

[___] = msesim(adaptFilt,x,m) specifies an optional decimation factor for computing mse, meanw, and tracek. If m > 1, every mth value of each of these sequences is saved. If omitted, the value of m defaults to 1.

Examples

collapse all

Open Live Script

The mean squared error (MSE) measures the average of the squares of the errors between the desired signal and the primary signal input to the adaptive filter. Reducing this error converges the primary input to the desired signal. Determine the predicted value of MSE and the simulated value of MSE at each time instant using the msepred and msesim functions. Compare these MSE values with each other and with respect to the minimum MSE and steady-state MSE values. In addition, compute the sum of the squares of the coefficient errors given by the trace of the coefficient covariance matrix.

Initialization

Create a dsp.FIRFilter System object™ that represents the unknown system. Pass the signal, x, to the FIR filter. The output of the unknown system is the desired signal, d, which is the sum of the output of the unknown system (FIR filter) and an additive noise signal, n.

num = fir1(31,0.5);
fir = dsp.FIRFilter('Numerator',num);  
iir = dsp.IIRFilter('Numerator',sqrt(0.75),...
        'Denominator',[1 -0.5]);
x = iir(sign(randn(2000,25))); 
n = 0.1*randn(size(x));           
d = fir(x) + n;

LMS Filter

Create a dsp.LMSFilter System object to create a filter that adapts to output the desired signal. Set the length of the adaptive filter to 32 taps, step size to 0.008, and the decimation factor for analysis and simulation to 5. The variable simmse represents the simulated MSE between the output of the unknown system, d, and the output of the adaptive filter. The variable mse gives the corresponding predicted value.

l = 32;
mu = 0.008;
m  = 5;

lms = dsp.LMSFilter('Length',l,'StepSize',mu);
[mmse,emse,meanW,mse,traceK] = msepred(lms,x,d,m);
[simmse,meanWsim,Wsim,traceKsim] = msesim(lms,x,d,m);

Plot the MSE Results

Compare the values of simulated MSE, predicted MSE, minimum MSE, and the final MSE. The final MSE value is given by the sum of minimum MSE and excess MSE.

nn = m:m:size(x,1);
semilogy(nn,simmse,[0 size(x,1)],[(emse+mmse)...
    (emse+mmse)],nn,mse,[0 size(x,1)],[mmse mmse])
title('Mean Squared Error Performance')
axis([0 size(x,1) 0.001 10])
legend('MSE (Sim.)','Final MSE','MSE','Min. MSE')
xlabel('Time Index')
ylabel('Squared Error Value')

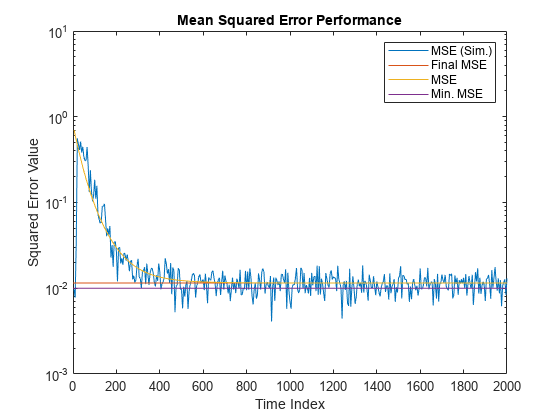
Figure contains an axes object. The axes object with title Mean Squared Error Performance, xlabel Time Index, ylabel Squared Error Value contains 4 objects of type line. These objects represent MSE (Sim.), Final MSE, MSE, Min. MSE.

The predicted MSE follows the same trajectory as the simulated MSE. Both these trajectories converge with the steady-state (final) MSE.

Plot the Coefficient Trajectories

meanWsim is the mean value of the simulated coefficients given by msesim. meanW is the mean value of the predicted coefficients given by msepred.

Compare the simulated and predicted mean values of LMS filter coefficients 12,13,14, and 15. 

plot(nn,meanWsim(:,12),'b',nn,meanW(:,12),'r',nn,...
meanWsim(:,13:15),'b',nn,meanW(:,13:15),'r')
PlotTitle ={'Average Coefficient Trajectories for';...
            'W(12), W(13), W(14), and W(15)'}
PlotTitle = 2x1 cell
    {'Average Coefficient Trajectories for'}
    {'W(12), W(13), W(14), and W(15)'      }


title(PlotTitle)
legend('Simulation','Theory')
xlabel('Time Index')
ylabel('Coefficient Value')

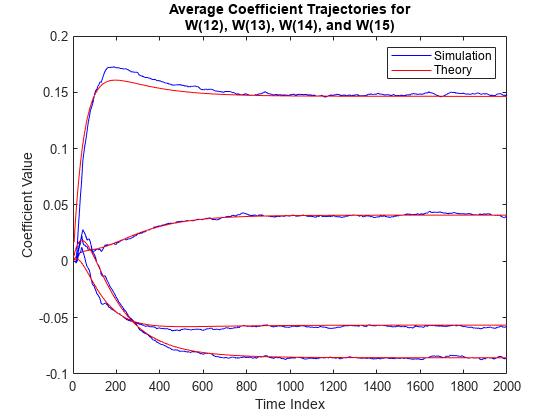
Figure contains an axes object. The axes object with title Average Coefficient Trajectories for W(12), W(13), W(14), and W(15), xlabel Time Index, ylabel Coefficient Value contains 8 objects of type line. These objects represent Simulation, Theory.

In steady state, both the trajectories converge.

Sum of Squared Coefficient Errors

Compare the sum of the squared coefficient errors given by msepred and msesim. These values are given by the trace of the coefficient covariance matrix.

semilogy(nn,traceKsim,nn,traceK,'r')
title('Sum-of-Squared Coefficient Errors')
axis([0 size(x,1) 0.0001 1])
legend('Simulation','Theory')
xlabel('Time Index')
ylabel('Squared Error Value')

Figure contains an axes object. The axes object with title Sum-of-Squared Coefficient Errors, xlabel Time Index, ylabel Squared Error Value contains 2 objects of type line. These objects represent Simulation, Theory.

Open Live Script

Identify an unknown system by performing active noise control using a filtered-x LMS algorithm. The objective of the adaptive filter is to minimize the error signal between the output of the adaptive filter and the output of the unknown system (or the system to be identified). Once the error signal is minimal, the unknown system converges to the adaptive filter.

Initialization

Create a dsp.FIRFilter System object that represents the system to be identified. Pass the signal, x, to the FIR filter. The output of the unknown system is the desired signal, d, which is the sum of the output of the unknown system (FIR filter) and an additive noise signal, n.

num = fir1(31,0.5);
fir = dsp.FIRFilter('Numerator',num);  
iir = dsp.IIRFilter('Numerator',sqrt(0.75),...
        'Denominator',[1 -0.5]);
x = iir(sign(randn(2000,25))); 
n = 0.1*randn(size(x));           
d = fir(x) + n;

Adaptive Filter

Create a dsp.FilteredXLMSFilter System object to create an adaptive filter that uses the filtered-x LMS algorithm. Set the length of the adaptive filter to 32 taps, step size to 0.008, and the decimation factor for analysis and simulation to 5. The variable simmse represents the error between the output of the unknown system, d, and the output of the adaptive filter. 

l = 32;                         
mu = 0.008;                     
m  = 5;                         
fxlms = dsp.FilteredXLMSFilter(l,'StepSize',mu); 
[simmse,meanWsim,Wsim,traceKsim] = msesim(fxlms,x,d,m);
plot(m*(1:length(simmse)),10*log10(simmse))
xlabel('Iteration')
ylabel('MSE (dB)')
% Plot the learning curve for filtered-x LMS filter 
% used in system identification
title('Learning curve')

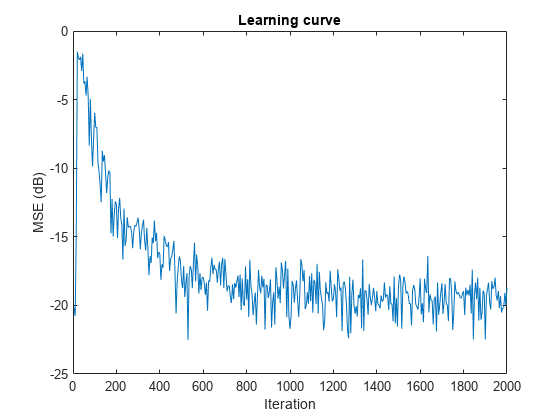
Figure contains an axes object. The axes object with title Learning curve, xlabel Iteration, ylabel MSE (dB) contains an object of type line.

With each iteration of adaptation, the value of simmse decreases to a minimal value, indicating that the unknown system has converged to the adaptive filter.

Open Live Script
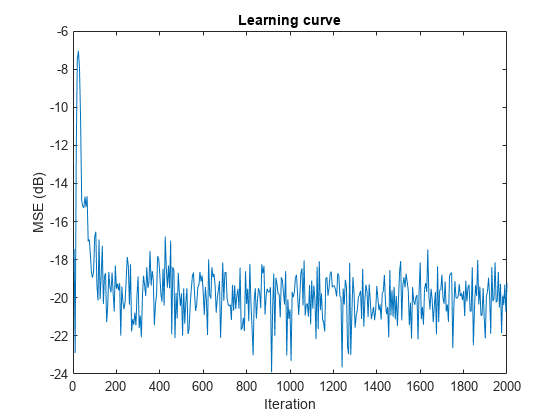
ha = fir1(31,0.5);
% FIR system to be identified 
fir = dsp.FIRFilter('Numerator',ha); 
iir = dsp.IIRFilter('Numerator',sqrt(0.75),...
        'Denominator',[1 -0.5]);
x = iir(sign(randn(2000,25))); 
% Observation noise signal 
n = 0.1*randn(size(x)); 
 % Desired signal 
d = fir(x)+n;
% Filter length 
l = 32;
% Decimation factor for analysis
% and simulation results 
m  = 5;                             
ha = dsp.AdaptiveLatticeFilter(l); 
[simmse,meanWsim,Wsim,traceKsim] = msesim(ha,x,d,m);
plot(m*(1:length(simmse)),10*log10(simmse));
xlabel('Iteration'); 
ylabel('MSE (dB)');
% Plot the learning curve used for 
% adaptive lattice filter used in system identification
title('Learning curve')

Figure contains an axes object. The axes object with title Learning curve, xlabel Iteration, ylabel MSE (dB) contains an object of type line.

Open Live Script
fir = fir1(31,0.5);
% FIR system to be identified 
firFilter = dsp.FIRFilter('Numerator',fir); 
iirFilter = dsp.IIRFilter('Numerator',sqrt(0.75),...
        'Denominator',[1 -0.5]);
x = iirFilter(sign(randn(2000,25))); 
% Observation noise signal 
n = 0.1*randn(size(x)); 
% Desired signal 
d = firFilter(x)+n; 
% Filter length 
l = 32;       
% Block LMS Step size
mu = 0.008;  
% Decimation factor for analysis
% and simulation results 
m  = 32;                            
fir = dsp.BlockLMSFilter(l,'StepSize',mu); 
[simmse,meanWsim,Wsim,traceKsim] = msesim(fir,x,d,m);
plot(m*(1:length(simmse)),10*log10(simmse));
xlabel('Iteration'); ylabel('MSE (dB)');
% Plot the learning curve for 
% block LMS filter used in system identification
title('Learning curve')

Figure contains an axes object. The axes object with title Learning curve, xlabel Iteration, ylabel MSE (dB) contains an object of type line.

Open Live Script
ha = fir1(31,0.5);
% FIR system to be identified 
fir = dsp.FIRFilter('Numerator',ha); 
iir = dsp.IIRFilter('Numerator',sqrt(0.75),...
        'Denominator',[1 -0.5]);
x = iir(sign(randn(2000,25))); 
% Observation noise signal 
n = 0.1*randn(size(x));         
% Desired signal 
d = fir(x)+n;  
% Filter length 
l = 32;  
% Affine Projection filter Step size. 
mu = 0.008;
% Decimation factor for analysis
% and simulation results 
m  = 5;                             
                                    
apf = dsp.AffineProjectionFilter(l,'StepSize',mu); 
[simmse,meanWsim,Wsim,traceKsim] = msesim(apf,x,d,m);
plot(m*(1:length(simmse)),10*log10(simmse));
xlabel('Iteration'); ylabel('MSE (dB)');
% Plot the learning curve for affine projection filter 
% used in system identification
title('Learning curve')

Figure contains an axes object. The axes object with title Learning curve, xlabel Iteration, ylabel MSE (dB) contains an object of type line.

Input Arguments

collapse all

Adaptive filter, specified as one of the following System objects:

Input signal, specified as a scalar, column vector, or matrix. Columns of the matrix x contain individual input signal sequences. The input, x, and the desired signal, d, must have the same size and data type.

If adaptFilt is a dsp.BlockLMSFilter object, the input signal frame size must be greater than or equal to the value you specify in the BlockSize property of the object.

Data Types: single | double

Desired response signal, specified as a scalar, column vector, or matrix. Columns of the matrix d contain individual desired signal sequences. The input, x, and the desired signal, d, must have the same size and the data type.

If adaptFilt is a dsp.BlockLMSFilter System object, the desired signal frame size must be greater than or equal to the value you specify in the BlockSize property of the object.

Data Types: single | double

Decimation factor, specified as a positive scalar. Every mth value of the estimated sequences is saved into the corresponding output arguments, mse, meanw, w, and tracek. If m equals 1, every value of these sequences is saved.

If adaptFilt is a dsp.BlockLMSFilter System object, the decimation factor must be a multiple of the value you specify in the BlockSize property of the object.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical

Output Arguments

collapse all

Estimates of the mean squared error of the adaptive filter at each time instant, returned as a column vector.

If the adaptive filter is dsp.BlockLMSFilter and the decimation factor m is specified, length of mse equals floor(M/m). M is the frame size (number of rows) of the input signal, x. If m is not specified, the length of mse equals floor(M/B), where B is the value you specify in the BlockSize property of the object. The input signal frame size must be greater than or equal to the value you specify in the BlockSize property of the object. The decimation factor, if specified, must be a multiple of the BlockSize property.

For the other adaptive filters, if the decimation factor, m = 1, the length of mse equals the frame size of the input signal. If m > 1, the length of mse equals floor(M/m).

Data Types: double

Sequence of coefficient vector means of the adaptive filter at each time instant, estimated as a matrix. The columns of this matrix contain estimates of the mean values of the adaptive filter coefficients at each time instant.

If the adaptive filter is dsp.BlockLMSFilter and the decimation factor m is specified, the dimensions of meanw is floor(M/m)-by-N. M is the frame size (number of rows) of the input signal, x. N is the length of the filter weights vector, specified by the Length property of the adaptive filter. If m is not specified, the dimensions of meanw is floor(M/B)-by-N, where B is the value you specify in the BlockSize property of the object. The input signal frame size must be greater than or equal to the value you specify in the BlockSize property of the object. The decimation factor, if specified, must be a multiple of the BlockSize property.

For the other adaptive filters, If the decimation factor, m = 1, the dimensions of meanw is M-by-N. If m > 1, the dimensions of meanw is floor(M/m)-by-N.

Data Types: double

Final values of the adaptive filter coefficients for the algorithm corresponding to adaptFilt, returned as a row vector. The length of the row vector equals the value you specify in the Length property of the object.

Data Types: single | double

Sequence of total coefficient error powers, estimated as a column vector. This column vector contains estimates of the total coefficient error power of the adaptive filter at each time instant.

If the adaptive filter is dsp.BlockLMSFilter and the decimation factor m is specified, length of tracek equals floor(M/m). M is the frame size (number of rows) of the input signal, x. If m is not specified, the length of tracek equals floor(M/B), where B is the value you specify in the BlockSize property of the object. The input signal frame size must be greater than or equal to the value you specify in the BlockSize property of the object. The decimation factor, if specified, must be a multiple of the BlockSize property.

For the other adaptive filters, if the decimation factor, m = 1, the length of tracek equals the frame size of the input signal. If m > 1, the length of tracek equals floor(M/m).

Data Types: double

References

[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.

Version History

Introduced in R2012a

See Also

Functions

Objects

Topics