Raised Cosine Transmit Filter
Apply pulse shaping by interpolating signal using raised cosine FIR filter
Libraries:
Communications Toolbox /
Comm Filters
Communications Toolbox HDL Support /
Comm Filters
Description
The Raised Cosine Transmit Filter block applies pulse shaping by interpolating an input signal using a raised cosine finite impulse response (FIR) filter. The FIR filter has (Filter span in symbols × Output samples per symbol + 1) tap coefficients. The block icon shows the impulse response of the filter. For more information, see Algorithms.
Examples
The Raised Cosine Transmit Filter and Raised Cosine Receive Filter blocks are designed for raised cosine (RC) filtering. Each block can apply a square-root raised cosine (RRC) filter or a raised cosine filter to a signal. You can vary the roll-off factor and span of the filter.
The Raised Cosine Transmit Filter and Raised Cosine Receive Filter blocks are tailored for use at the transmitter and receiver, respectively. The transmit filter upsamples (interpolates) the output signal. The receive filter expects its input signal to be upsampled and downsamples (decimates) the output signal, based on the configured settings of the block.
The raised cosine transmit and receive filter blocks each introduce a propagation delay, as described in Group Delay.
The doc_rrcfiltercompare.slx model shows how to split the filtering equally between the transmitter and the receiver by using a pair of square root raised cosine filters. The use of a matched pair of square root raised cosine filters is equivalent to a single normal raised cosine filter. The filters share the same span and use the same number samples per symbol but the two filter blocks on the upper path have a square root shape and the single filter block on the lower path has the normal shape.

Run the model and observe the eye and constellation diagrams. The performance is nearly identical for the two methods. Note that the limited impulse response of practical square root raised cosine filters causes a slight difference between the response of two cascaded square root raised cosine filters and the response of one raised cosine filter.




Apply root raised cosine filtering to a QPSK-modulated signal. Compute the variance of the filtered signal. Plot the signal before and after filtering.
In the cm_tx_rrc_filter model, a binary is QPSK modulated and then root raised cosine filtered with the oversampling rate set to 8 and the roll-off factor set to 0.2.

The signal level reduces by a factor of one over the oversample rate. Since the QPSK-modulated signal has unity power and the transmit RRC filtering oversamples the signal by 8, the Variance block after the transmit filtering computes a variance level of approximately 1/8.
Computed variance = 0.1248

Apply raised cosine matched filtering to a modulated signal by applying transmit and receive root raised cosine (RRC) filtering to the input signal. Demonstrate input signal power adjustment for correct SNR and the delay adjustment for correct error rate calculation.
The cm_tx_rx_rrc_filter model outputs frames of random integers by using a Random Integer Generator block. The frames of data pass through a QPSK Modulator Baseband block, Raised Cosine Transmit Filter, AWGN Channel block, Raised Cosine Receive Filter, and QPSK Demodulator Baseband block. Separate Error Rate Calculation blocks compute the bit error rate after QPSK demodulation, with and without accounting for the delay of the received signal due to the transmit and receive filtering.
The model initializes the variables that configure block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink). The model demonstrates configuration of parameters to set the input signal power level for AWGN based on filter oversampling, and to set the delay for the error rate calculation path based on the filter delay.

The QPSK-modulated signal has unity power, but signal oversampling by the transmit RRC filtering reduces the signal level by the oversampling rate. To apply the correct noise level, you must adjust the input signal power in the AWGN block to account for the reduced signal level due to oversampling by the filter. A Variance block computes a variance to be approximately one over the oversampling rate, 1/8.
Computed variance = 0.1250

A Time Scope plots the Received, Delayed, and Not delayed signals. The Delayed signal aligns with the Received signal, but the Not delayed signal is shifted by 10 samples. The error rate calculation shows the correct BER when you account for the filter delay.
Delay not accounted for: BER = 0.75 Delay accounted for: BER = 0.00462
Extended Examples
Frame Synchronization Using Barker Code Preamble
Use a length 13 Barker code frame preamble for frame synchronization of data bits.
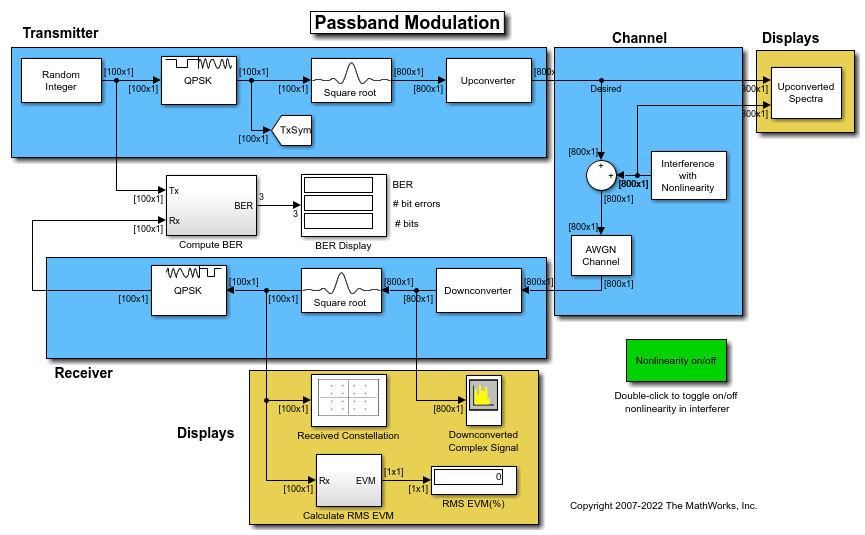
Passband Modulation
Simulate passband modulation by multiplying a modulated complex signal with a complex sine wave to perform frequency upconversion.
Ports
Input
Input signal, specified as a scalar, column vector, or Ki-by-N matrix. Ki is the number of input samples per signal channel, and N is the number of signal channels.
Data Types: double | single | fixed point
Output
Output signal, returned as a scalar, column vector, or matrix. The block filters each channel over time and generates a Ko-by-N output matrix. The output signal is the same data type as the input signal.
Ko = Ki × L.
N is the number of signal channels.
Ki is the number of input samples per signal channel.
L is the value you specify in the Output samples per symbol parameter.
Data Types: double | single | fixed point
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Main
Filter shape, specified as Square root or
Normal. For more information, see Filter Characteristics.
Roll-off factor of the filter, specified as a scalar in the range [0,
1].
Filter span in symbols, specified as an even positive integer. The block truncates the infinite impulse response length of the ideal raised cosine filter to an FIR with a length equal to the value of this parameter.
Number of output samples per symbol, specified as an integer value greater
than 1. The number of taps for the raised cosine filter
equals the value of this parameter multiplied by the value of the Filter
span in symbols parameter.
Linear filter gain, specified as a positive scalar. The block scales the normalized filter coefficients by the linear filter gain value that you specify.
Input processing control, specified as one of these options:
Columns as channels (frame based)— The block treats each column of the input as a separate channel.Elements as channels (sample based)— The block treats each element of the input as a separate channel.
Block processing rate for input signal upsampling and filtering, specified as one of these options:
Enforce single-rate processing— When you select this option, the block maintains the input sample rate and processes the signal by increasing the output frame size by a factor of N.Allow multirate processing— When you select this option, the block processes the signal such that the output sample rate is N times faster than the input sample rate.
Dependencies
To use Enforce single-rate processing, you must set
Input processing to Columns as channels
(frame based).
Select this parameter to save the filter coefficients as the MATLAB® workspace variable that you specify in the Coefficient variable name parameter.
Name of the coefficient variable to create in the MATLAB workspace.
Dependencies
This parameter appears when you select Export filter coefficients to workspace.
To analyze the raised cosine filter response, click the View Filter Response button. MATLAB opens a filter visualization window. When you change the block mask parameter settings, click the button again to open a new instance of the window and see the new filter characteristics. Previous filter visualization windows remain open and reflect your previous mask settings. Instances of the filter visualization window remain open after you close the model.
Data Types
Select the rounding mode for fixed-point operations. The block uses
rounding mode when the result of a fixed-point calculation does not map
exactly to a number representable by the data type. The filter coefficients
do not obey this parameter; they always round to
Nearest. For more information, see Rounding Modes
or Rounding Mode: Simplest (Fixed-Point Designer).
Select the overflow mode for fixed-point operations. The filter coefficients do not obey this parameter; they are always saturated.
Specify the word length and the fraction length of the filter coefficients (numerator and denominator).
This block is a subsystem that contains a FIR Interpolation block. For diagrams showing the use of the coefficient data types in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block.
When you select Inherit: Same word length as input, the word
length of the filter coefficients match that of the input to the block. In
this mode, the fraction length of the coefficients is automatically set to
the binary-point only scaling that provides you with the best precision
possible given the value and word length of the coefficients.
The filter coefficients do not obey the Rounding
mode and the Saturate
on integer overflow parameters; they are always saturated
and rounded to Nearest.
For information about specifying data types, see Data Type Assistant.
Specify the product output word and fraction lengths. For diagrams showing the use of the product output data type in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block and Multiplication Data Types.
When you select
Inherit via internal rule, the block inherits the data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.When you select
Inherit: Same as input, these characteristics match those of the input to the block.
For information about specifying data types, see Data Type Assistant.
Specify the accumulator word and fraction lengths. For diagrams showing the use of the accumulator data type in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block and Multiplication Data Types.
When you select
Inherit: Inherit via internal rule, the block inherits the data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule.When you select
Inherit: Same as input, these characteristics match those of the input to the block.When you select
Inherit: Same as product output, these characteristics match those of the product output.
For information about specifying data types, see Data Type Assistant.
Specify the output word and fraction lengths.
When you select
Inherit: Same as input, these characteristics match those of the input to the block.When you select
Inherit: Same as accumulator, these characteristics match those of the accumulator.When you select
Inherit: Same as product output, these characteristics match those of the product output.
For information about specifying data types, see Data Type Assistant.
Select this parameter to prevent the fixed-point tools from overriding the data types that you specify in the block dialog box. For more information, see the Fixed-Point Tool (Fixed-Point Designer).
Block Characteristics
More About
The Data Type Assistant helps you set data
attributes. To use the Data Type Assistant, click ![]() . For more information, see Specify Data Types Using Data Type Assistant (Simulink).
. For more information, see Specify Data Types Using Data Type Assistant (Simulink).
Tips
Exporting Filter Coefficients to the MATLAB Workspace
To examine or manipulate the coefficients of the filter that this block designs, select Export filter coefficients to workspace. Set the Coefficient variable name parameter to the name of a variable that you want the block to create in the MATLAB workspace. Running the simulation causes the block to create the variable, overwriting any previous contents in case the variable already exists.
Algorithms
Characteristics of the raised cosine receive filter are the same as in the Raised Cosine Receive Filter block, except that for transmit filtering, the input response length of the filter depends on the value of the Output samples per symbol parameter.
The Filter
shape parameter determines which type of filter the block uses;
choices are Normal and Square
root.
The impulse response of a normal raised cosine filter with roll-off factor R and symbol period T is
The impulse response of a square root raised cosine filter with roll-off factor R is
The impulse response of a square root raised cosine filter convolved with itself is approximately equal to the impulse response of a normal raised cosine filter.
Unlike an ideal raised cosine filter, which has an infinite impulse response (IIR), the block is an FIR filter and truncates the impulse response to the number of symbols that the Filter span in symbols parameter specifies. The impulse response length of the filter is (L×N + 1), where N is the Filter span in symbols parameter value and L is the Output samples per symbol parameter value.
The Rolloff
factor, R, determines the excess bandwidth of the
filter. R must be in the range [0,
1]. For example, a roll-off factor of 0.5
means that the bandwidth of the filter is 1.5 times the input sampling
frequency.
The block normalizes the filter coefficients to unit energy. If you specify a Linear amplitude
filter gain value other than 1, then the block
scales the normalized filter coefficients using the gain value you specify.
The input must be a discrete-time signal. This block accepts a column vector or matrix input signal.
The method selected for Rate options and the value of Output samples per symbol, L, determine the characteristics of the output signal.
When you set the Rate
options parameter to Enforce single-rate
processing, the input and output of the block have the same
sample rate. To generate the output while maintaining the input sample rate, the
block resamples the data in each column of the input such that the frame size of
the output (Mo) is
L times larger than that of the input
(M
o=
Mi×L), where
L represents the value of the Output samples
per symbol parameter.
When you set the Rate
options parameter to Allow multirate
processing, the input and output of the block are the same
size. However, the sample rate of the output is L times
faster than that of the input (that is, the output sample time is
1/L times the input sample time). When the block is in
multirate processing mode, you must also specify a value for the Input
processing parameter.
When you set the Input processing parameter to
Elements as channels (sample based), the block treats an M-by-L matrix input as M×N independent channels, and processes each channel over time. The output sample period, Tso, is L times shorter than the input sample period (Tso = Tsi/L), while the input and output sizes remain identical.When you set the Input processing parameter to
Columns as channels (frame based), the block treats an Mi-by-N matrix input as N independent channels. The block processes each column of the input over time by keeping the frame size constant (Mi=Mo), while making the output frame period, Tfo, L times shorter than the input frame period (Tfo = Tfi / L).
Extended Capabilities
Generated code relies on memcpy or
memset functions (string.h) under certain
conditions.
This block supports SIMD code generation using Intel® AVX2 technology under these conditions:
Input processing is set to
Columns as channels (frame based).Rate options is set to
Enforce single-rate processing.Input signal is real-valued with real filter coefficients.
Input signal is complex-valued with real or complex filter coefficients.
Input signal has a data type of
singleordouble.
The SIMD technology significantly improves the performance of the generated code. For details, see Generate SIMD Code from Simulink Blocks for Intel Platforms (Embedded Coder).
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block is a subsystem that contains an FIR Interpolation block. You can set HDL Properties on the subsystem, or you can look under the mask and set HDL Properties on the filter block. See the "HDL Code Generation" section of the Subsystem, Atomic Subsystem, CodeReuse Subsystem (Simulink) and FIR Interpolation block reference pages for a list of properties.
To save setting changes under the mask, you must break the library link. To break the library link, select the Raised Cosine Transmit Filter block and run this command.
set_param(gcb,'LinkStatus','inactive')
Version History
Introduced before R2006a
See Also
Apps
Blocks
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)