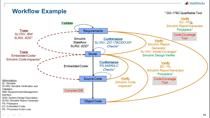
Model-Based Optimization of a Solar-Powered Car
Arjo van der Ham, Lightyear
Lightyear One is a remarkable innovation: It is an all-wheel drive, five-seater electric car charged by the sun. The key challenge of this innovation is matching the energy required while driving, with the limited and fluctuating energy yield of the solar panels. MathWorks solutions are used by Lightyear engineers as the “Swiss Army knife” to address this challenge, optimizing the energy flow from the solar panel and its accompanying electronics to the vehicle. This presentation provides an overview of Lightyear’s accomplishments to date, and its ongoing mission: clean mobility for everyone.
Recorded: 20 May 2019
Welcome, everyone. I'm Arjo van der Ham, co-founder and CTO of Lightyear. And today marks roughly my 10-year anniversary with MATLAB. And I would like to take you through it, a little bit, what we've been doing.
This is one of the first things I did. It started in my first year of studying electrical engineering here at the University Eindhoven. And we used this automated test script to measure the collector emitter voltage of bipolar transistors. And throughout the years, throughout all the years, I began to really see the added value of MATLAB as a universal tool, also in my personal life.
So I did a lot of Monte Carlo simulations, 10,000 for each data point in the matrix, to calculate the chance of winning a battle in the board game of Risk. I haven't lost since. So I can only advise you to do the same, or make it even a bit smarter.
But of course, we've also been doing more serious stuff, such as this, for example. This is a user interface made with the tool to control a new topology for a power converter for a motor inverter. But I've also been building lots of similar models for control systems using Simscape modeling the dynamics of a six-degree-of-freedom flight simulator, that sort of stuff.
But in the end, what I really used MATLAB for the most was this. It's my regular old desktop calculator. I guess what I'm trying to say is the way I see MATLAB is really as this Swiss army knife for engineers. You name it, and it will do it. And that's also how we're using it at Lightyear at the moment to realize our mission of clean mobility for everyone. Please enjoy the video.
Earth, our beautiful little planet—a place to live, to discover, to travel. As humans we have always loved to move around. For thousands of years, we've done it using the energy that mother nature gave us. We discovered that we could go further and faster by digging up and burning what nature had created.
And, now we travel the planet like never before. The total distance we cover each year using fossil fuels is just over 9.5 trillion kilometers, one light year. Our goal is to let people travel the same distance using only the power of nature before the year 2035.
We set out to develop a car that directly uses nature's biggest source of energy, the sun. It is here today, tomorrow, and it will be here forever. As pioneers in this field, we have been building prototypes for years with great success. And now, it's time for a giant leap.
Traveling the distance of a light year using only solar energy—that is our mission.
So our mission is to create clean mobility for everyone. But why do we do that, actually? Well, if we look at the situation as it is today, only about 3% of the world population has access to a public charging station within a range of about 100 kilometers. And having to develop charging stations is really limiting the adoption of electric vehicles. And actually, the solution, as it's sort of proposed by everyone right now, it roughly looks like this.
So first we have to replace all the coal-fired power plants with renewable energy. We have to give the electricity grid a serious upgrade. Everybody has to install home batteries and solar panels. We have to install about a billion charging stations around the world. And then all of you still also have to buy this electric car.
And what we propose is to try and skip as many of these expensive infrastructure investments as we can and get the energy that the car needs as directly as we can from the solar panel on the car, from the sun. And to show you that that is already possible today, we're developing the Lightyear One. And the Lightyear One is a five-seater electric car. It's really designed for efficiency, to drive as efficiently as possible.
It has a solar panel on the roof, the hood, and the trunk. And the solar panel will give you up to 10,000 kilometers of range per year in the Netherlands. And if you go to a more sunny place, if you go to Spain or something, I think it's about 1 1/2 times as much. If you go to California, it's twice as much. And that's nice. But what does that mean in practice if you drive this car on a daily basis?
Well, imagine going on a surf trip by the coast of Portugal. You drive 1,100 kilometers up and down the coast. You collapse the rear bench, put in your surfboards, or your bike, or golf bag, skis, whatever. It all fits. And you don't have to recharge once if you take two weeks to do the trip. And that's really the freedom that this sort of car can give you as a user.
Of course, I'm not doing that myself. So we now have a team of about 130 engineers at the automotive campus in Helmond. And it's really a combination between young talents and industry experience to get to the right balance.
And we get a lot of help from partners. Especially, we try to focus on the things that really make the car special, to do ourselves. And the more traditional automotive engineering stuff, we try to do with a lot of partners from the industry.
But also, we're being helped a lot by investors and by even the first customers as well. So up until now, we've already received more than 80 down payments for the Lightyear One. And the company's funded by roughly 60 private investors until now.
And of course, I think most of you are technical people. So you're wondering, but how do we actually get there? How do you make this happen? Of course, I have to tell you a little bit about that. And step one is start from a clean sheet.
So imagine that the blue bar is the energy consumption of a current electric vehicle, and the yellow bar is the amount of energy yield you could get from a solar panel if you put it on the shape of the conventional car. And what we really try to do is match the two. How do we do that? Also a number of steps.
So the first one is make the car lighter, just using lightweight materials to reduce the energy consumption. And because you do that, you need a smaller battery and lighter motors to get to the same performance. So the car gets lighter even more. So you get into this downward spiral of lightweighting, which is really known from the aerospace industry as well.
At a certain point in time, you can reduce the weight of the car enough to develop enough torque using in-wheel motors. And these in-wheel motors, they add efficiency because you no longer need the final drive. You no longer need the differentials in between. And this gives you not only a lot of space, but also, in the long term, better maintenance, et cetera, because just less moving parts in the car. But it also gives us design freedom to improve the aerodynamics in the underbody.
And furthermore, we improve the aerodynamics by adding wheel spats on the rear wheels, but also by replacing mirrors with cameras. And all together, this brings down energy consumption quite a bit. But it's not enough to make it match. So you also have to work on the other side. So what we do there is, first of all, it sounds very trivial, but make the solar panel bigger. It sounds very trivial, but it is one of the reasons that you have to start with a clean sheet and make sure that, actually, the car has the shape to put all these solar panels on it.
And furthermore, we increase the efficiency of the electronics that convert the solar energy into the battery. And that's what I want to dive into a little bit deeper because I'm also a technical guy, and I can't resist to tell you about it.
So we're going to take a small step back and see how we did it in the Solar Challenge in all those years. And there, the current state of the art looked like this. So we had a bunch of solar cells on the car. And about 125 of them would be connected in series. And then there would be one central converter that converts it to the battery.
The main disadvantage of this is that the cell receiving the least amount of sunlight, the weakest cell, is limiting the current through the string, for all the electrical engineers in the group. And these mismatches—you get them from shadows, but also from curvature, because there's always one cell receiving less sunlight if you have this curved surface.
And therefore, we always used to build, for the rays, we used to build cars with flat roofs. And this flat roof, we don't really like it because it's limiting the design freedom that you have as a designer, but also, the aerodynamic performance. So for us, it was clear. If we're going to develop a commercial car, this is one of the bridges we need to cross, what we need to fix.
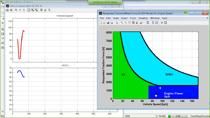
So but first, how big is this problem, actually, to give you an idea? So to investigate how big the effect is of the curvature against the number of cells, we defined this grouping efficiency as the ratio between the amount of power that you get from the grouped cells versus the amount of power that I would get if I would be able to operate each individual cell at its own maximum power point.
To give you an idea, if we have this flat roof of Stella, it is a little bit of a curve in the end. That's why it's not 100%. You get a grouping efficiency of about 98.6%. And if you have this very curvy Volkswagen Beetle, you lose 25% of the available energy, which is a bit too much and be a shame, of course. The solution is pretty straightforward. You want to go to smaller groups, less cells in series. And this is called distributed maximum power point tracking.
How does that work? Roughly like this. So we have the old situation, all the cells connected to series. And then imagine that each solar cell you see here is actually a small group of solar cells connected in series. Let's say that all of these groups, one group received less sunlight because it's curved or because there's a shadow, and the other two, they each receive 12.
If you just connect it like this, then the bottom group would be limiting the current through the top groups. And therefore, we can only get 18 watts. Of the total available 30 watts at the output, we can only get 18 watts at the output. So about half the energy is lost. This is a bit to shame, of course.
The traditional solution is to place this bypass diode. And using the bypass diode, we sort of shut down the group that's limiting. And thereby, we allow the other two groups to deliver the full 12 watts to the output. And we get 24 at the output, but it's still not 30.
So what do we do with this with maximum power point tracking is we add a balancing converter to each group. And the outputs of these balancing converters are connected in parallel. And then we control them in such a way that each of these converters that's connected to a stronger group gets a little bit of power from the strong groups through the bus. And the converters that are connected to the weaker groups, they take a little bit of power back from the bus and send it to the groups so that in the end, the net amount of power coming from each group is equal.
And now there's no limit in current anymore, and we can get all of the 30 watts at the output of the car—of course, if we assume that all those converts are lossless, which is not the case, but the effect is not that big, as we will see. In the steady state, so all the groups are at the maximum power point, and the net power going through that bus is zero.
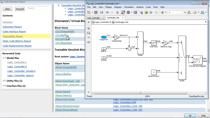
And now for us the question was, system is nice, but how many of these cells do we now have to place in each group to come to a good balance between efficiency and cost, et cetera? And to investigate that, we made this entirely MATLAB based model where we start with a CAD file of the car. And this CAD file, we use an algorithm to place solar cells on the area of the car. So it looks roughly like that.
And then we cluster these solar cells into groups using a clustering algorithm. And then we combine that with Typical Model Year weather data, which is the same type of weather data that building engineers use to calculate climates in buildings, et cetera. And using that data, we can calculate exactly, for each individual solar cell, how much irradiance is coming onto each individual cell.
Using that, we can calculate the IV curve of each individual solar cell. And if we combine that with which cells are in which groups, we can compute the IV curves of all the individual groups. And now the ratio between the maximum power points of the IV curves of the groups and the maximum power points of the cells gives us this grouping efficiency that we've been talking about, group.
And then we run into a steady state model of the PV to isolate the bus architecture that we've shown in the previous slide to calculate beta. And beta is the ratio between the power that's being processed by the converters that we've added and the total amount of power going through the system. And you need that to calculate the efficiency of the system in the end.
I have to show you this as well because I always like to see algorithms work, so I couldn't resist putting it in. So how does this clustering algorithm work? Well, we need to cluster 76 points, so all of the solar cells into eight clusters of size nine or 10. And what we do is, first, we initialize randomly the clusters. And then each cluster can choose a cell that it wants in its group. So now, we do that a few times, and you see the groups created.
And yet there are not enough cells left to go to each group. So we allow the lost cells to choose which group they want to belong to. And now we have groups, but they're looking really shitty because, actually, you want those groups to be really close together because cells that are connected close together have roughly the same orientation. And therefore, you have less mismatches within that group, and you get a better grouping efficiency.
So what we now do is we shift so-called swap proposals. So each group can say, okay, I want to switch this cell with your cell over here. And if we both get better like that, so if the group gets smaller that way, then it's a good solution, and we do it. So start swapping, and you see the groups becoming more neat, and we keep on swapping until the solution no longer improves. And then we get the final groups.
We mainly use this algorithm because we wanted to investigate lots of different group sizes for lots of different cars. So you could have done this by hand as well, of course, but becomes a lot of work. For the final car, we are doing this by hand once it's one car, and we know exactly how big the groups need to be, mainly to optimize their electrical routing of all the cables, et cetera, and make it a bit more efficient in that way.
Now this algorithm, this entire simulation, we used to compare four cars. And of course, we also calculated the lighter one, but I'm not allowed to show it to you yet. So it's not on the slide.
But what I can tell you is we used two cars of a typical curvature. And the lighter one has roughly similar curvature to those two. So it's a Fiat Punto and the Tesla Model S. Then we used one car with a very flat roof, Stella, and one car with a very curved roof, the Volkswagen Beetle.
And if we compare them and run them through the simulation, these are roughly the results. So on the bottom axis, you see how many cells you put in each group. And there you see the grouping efficiency, so how much power we actually lose because of the curvature. And the first thing you see is that if we put one cell per group, then each cell can operate at its maximum power point, so the grouping efficiency is, by definition, 100%.
What you also see is that if the curvature of the car increases, then the grouping efficiency drops faster, which is what we expected, of course. And if we then look at how much power is actually being processed by those converters that we've introduced to make it more efficient, first thing you can see is that on the bottom, if you put all of the cells on the roof in one group, and I don't have any balancing converters anymore, so the amount of power that's being processed is zero. If I have more curvature, the amount of power that's being processed goes up.
But what's interesting to see is that the total amount of power being processed is actually around the 10% to 12% range, which means that only a small fraction of the power is actually processed by those converters to get the system in the steady state solution. And that means that the system is not that sensitive to the efficiency of those new converters that we've introduced.
If we look at the results, then—we've left the Fiat Punto out because it gave exactly the same results as the Tesla because of similar curvature—and we compare the old system with the new system for cars of increasing curvature, you can see that the efficiency is actually made up out of two numbers. So it's the grouping efficiency, that is about how big the effect of the curvature is, and the conversion efficiency, which is the efficiency in the top case, of the old system, of just that converter. And in the bottom case, the conversion efficiency consists of the efficiency of that converter, the efficiency of the balancing converters, and this beta figure, how much power is being processed by those new converters.
If you compare them, for a flat roof, this system makes absolutely no sense. So don't use it. Do you gain a very little bit of grouping efficiency, but you lose more on conversion efficiency than you gain. However, for more curved cars you see that the grouping efficiency is dropping really fast with traditional system. And then adding a little bit of actual losses on the conversion efficiency actually more than makes up for it.
And in total, we gain 15% points of power output on the car. And in practice, that means instead of driving 8,000 kilometers per year on the sun, it means 10,000 kilometers a year on the sun. In the end, the influence of the system is really big on the final design of the car. If you go to even more curvature, so the Volkswagen Beetle, it's even 18% points.
Now, okay, this all sounds really nice, of course. But I think all of you are also wondering, okay, but when do we get to see the car, and when is it going through the market? Well, it still only covers for a few more weeks. But we are presenting the first prototype of the car the 25th of June this year. And then at the end of 2020, the first deliveries are expected. And in 2021, we start ramping up the production, and we have the start of the new models. And to give you a little bit of the vibe of the company, I have one last video to close off with.
Wow, can you feel the buzz? I do. Ladies and gentlemen, I'm really thrilled. I think there's something in the air here. I would love to see this become really, really, really big.
I do think in a couple of years, when you see these cars on the streets, that a kid will turn his head and say, hey, look, Dad, a car from the future! And I think the best thing now is to show you the Lightyear One.
And yeah. I'm sorry you still have to wait a little bit. But on the 25th of June, it will be publicly shown, as well, what the car's going to look like. Thanks for your attention.