emd
Empirical mode decomposition
Description
[___] = emd(___,
performs the empirical mode decomposition with additional options specified by
one or more Name,Value)Name,Value pair arguments.
emd(___) plots the original signal, IMFs, and
residual signal as subplots in the same figure.
Examples
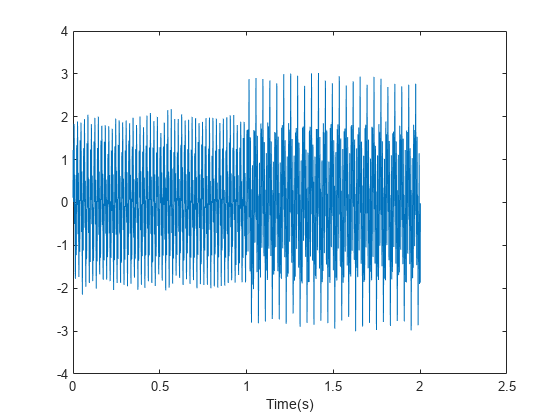
Load and visualize a nonstationary continuous signal composed of sinusoidal waves with a distinct change in frequency. The vibration of a jackhammer and the sound of fireworks are examples of nonstationary continuous signals. The signal is sampled at a rate fs.
load("sinusoidalSignalExampleData.mat","X","fs") t = (0:length(X)-1)/fs; plot(t,X) xlabel("Time (s)")

The mixed signal contains sinusoidal waves with different amplitude and frequency values.
To create the Hilbert spectrum plot, you need the intrinsic mode functions (IMFs) of the signal. Perform empirical mode decomposition to compute the IMFs and residuals of the signal. Since the signal is not smooth, specify 'pchip' as the interpolation method.
[imf,residual,info] = emd(X,Interpolation="pchip");The table generated in the command window indicates the number of sift iterations, the relative tolerance, and the sift stop criterion for each generated IMF. This information is also contained in info. You can hide the table by adding the 'Display',0 name value pair.
Create the Hilbert spectrum plot using the imf components obtained using empirical mode decomposition.
hht(imf,fs)

The frequency versus time plot is a sparse plot with a vertical color bar indicating the instantaneous energy at each point in the IMF. The plot represents the instantaneous frequency spectrum of each component decomposed from the original mixed signal. Three IMFs appear in the plot with a distinct change in frequency at 1 second.
This trigonometric identity presents two different views of the same physical signal:
.
Generate two sinusoids, s and z, such that s is the sum of three sine waves and z is a single sine wave with a modulated amplitude. Verify that the two signals are equal by calculating the infinity norm of their difference.
t = 0:1e-3:10; omega1 = 2*pi*100; omega2 = 2*pi*20; s = 0.25*cos((omega1-omega2)*t) + ... 2.5*cos(omega1*t) + ... 0.25*cos((omega1+omega2)*t); z = (2+cos(omega2/2*t).^2).*cos(omega1*t); norm(s-z,Inf)
ans = 3.2729e-13
Plot the sinusoids and select a 1-second interval starting at 2 seconds.
plot(t,[s' z']) xlim([2 3]) xlabel('Time (s)') ylabel('Signal')

Obtain the spectrogram of the signal. The spectrogram shows three distinct sinusoidal components. Fourier analysis sees the signals as a superposition of sine waves.
pspectrum(s,1000,'spectrogram','TimeResolution',4)
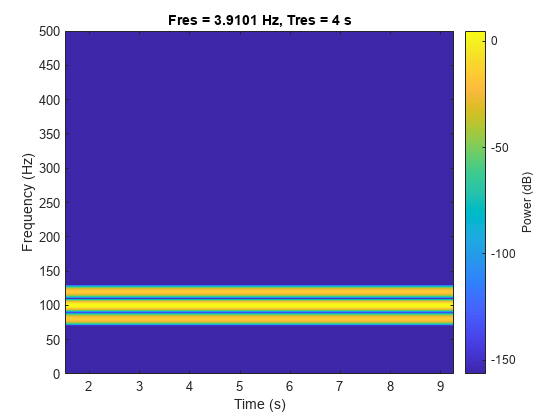
Use emd to compute the intrinsic mode functions (IMFs) of the signal and additional diagnostic information. The function by default outputs a table that indicates the number of sifting iterations, the relative tolerance, and the sifting stop criterion for each IMF. Empirical mode decomposition sees the signal as z.
[imf,~,info] = emd(s);
The number of zero crossings and local extrema differ by at most one. This satisfies the necessary condition for the signal to be an IMF.
info.NumZerocrossing - info.NumExtrema
ans = 1
Plot the IMF and select a 0.5-second interval starting at 2 seconds. The IMF is an AM signal because emd views the signal as amplitude modulated.
plot(t,imf) xlim([2 2.5]) xlabel('Time (s)') ylabel('IMF')

Simulate a vibration signal from a damaged bearing. Perform empirical mode decomposition to visualize the IMFs of the signal and look for defects.
A bearing with a pitch diameter of 12 cm has eight rolling elements. Each rolling element has a diameter of 2 cm. The outer race remains stationary as the inner race is driven at 25 cycles per second. An accelerometer samples the bearing vibrations at 10 kHz.
fs = 10000; f0 = 25; n = 8; d = 0.02; p = 0.12;
The vibration signal from the healthy bearing includes several orders of the driving frequency.
t = 0:1/fs:10-1/fs; a = 0.2*[1 0.5 0.2 0.1 0.05]; f = f0*[1 2 3 4 5]; yHealthy = a*sin(2*pi*f'.*t);
A resonance is excited in the bearing vibration halfway through the measurement process.
yHealthy = (1+1./(1+linspace(-10,10,length(yHealthy)).^4)).*yHealthy;
The resonance introduces a defect in the outer race of the bearing that results in progressive wear. The defect causes a series of impacts that recur at the ball pass frequency outer race (BPFO) of the bearing:
where is the driving rate, is the number of rolling elements, is the diameter of the rolling elements, is the pitch diameter of the bearing, and is the bearing contact angle. Assume a contact angle of 15° and compute the BPFO.
ca = 15; bpfo = n*f0/2*(1-d/p*cosd(ca));
Use the pulstran (Signal Processing Toolbox) function to model the impacts as a periodic train of 5-millisecond sinusoids. Each 3 kHz sinusoid is windowed by a flat top window. Use a power law to introduce progressive wear in the bearing vibration signal.
fImpact = 3000; tImpact = 0:1/fs:5e-3-1/fs; wImpact = flattopwin(length(tImpact))'/10; xImpact = sin(2*pi*fImpact*tImpact).*wImpact; tx = 0:1/bpfo:t(end); tx = [tx; 1.3.^tx-2]; nWear = 49000; nSamples = 100000; yImpact = pulstran(t,tx',xImpact,fs)/5; yImpact = [zeros(1,nWear) yImpact(1,(nWear+1):nSamples)];
Generate the BPFO vibration signal by adding the impacts to the healthy signal. Plot the signal and select a 0.3-second interval starting at 5.0 seconds.
yBPFO = yImpact + yHealthy; xLimLeft = 5.0; xLimRight = 5.3; yMin = -0.6; yMax = 0.6; plot(t,yBPFO) hold on [limLeft,limRight] = meshgrid([xLimLeft xLimRight],[yMin yMax]); plot(limLeft,limRight,"--") hold off xlabel("Time (seconds)") ylabel("Amplitude")

Zoom in on the selected interval to visualize the effect of the impacts.
xlim([xLimLeft xLimRight])

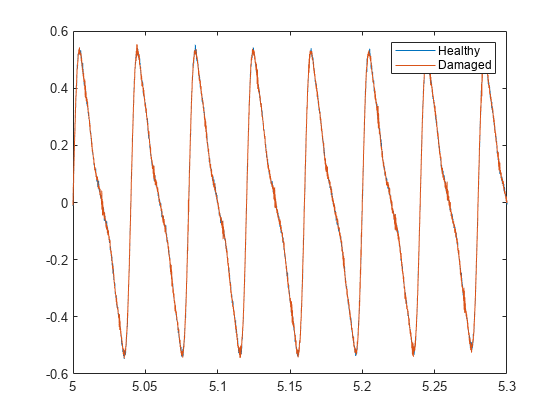
Add white Gaussian noise to the signals. Specify a noise variance of .
rn = 150; yGood = yHealthy + randn(size(yHealthy))/rn; yBad = yBPFO + randn(size(yHealthy))/rn; plot(t,yGood,t,yBad) xlim([xLimLeft xLimRight]) legend("Healthy","Damaged") xlabel("Time (seconds)") ylabel("Amplitude")
Use emd to perform an empirical mode decomposition of the healthy bearing signal. Compute the first five intrinsic mode functions (IMFs). Use the Display name-value argument to show a table with the number of sifting iterations, the relative tolerance, and the sifting stop criterion for each IMF.
imfGood = emd(yGood,MaxNumIMF=5,Display=1);
Current IMF | #Sift Iter | Relative Tol | Stop Criterion Hit
1 | 3 | 0.017132 | SiftMaxRelativeTolerance
2 | 3 | 0.12694 | SiftMaxRelativeTolerance
3 | 6 | 0.14582 | SiftMaxRelativeTolerance
4 | 1 | 0.011082 | SiftMaxRelativeTolerance
5 | 2 | 0.03463 | SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.
Use emd without output arguments to visualize the first three modes and the residual.
emd(yGood,MaxNumIMF=5)
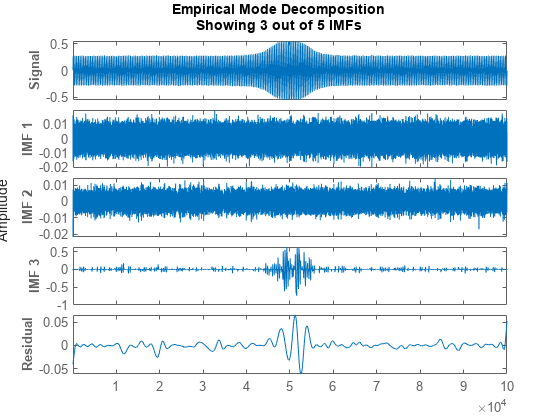
Compute and visualize the IMFs of the defective bearing signal. The first empirical mode reveals the high-frequency impacts. This high-frequency mode increases in energy as the wear progresses. The third mode shows the resonance in the vibration signal.
imfBad = emd(yBad,MaxNumIMF=5,Display=1);
Current IMF | #Sift Iter | Relative Tol | Stop Criterion Hit
1 | 2 | 0.041274 | SiftMaxRelativeTolerance
2 | 3 | 0.16695 | SiftMaxRelativeTolerance
3 | 3 | 0.18428 | SiftMaxRelativeTolerance
4 | 1 | 0.037177 | SiftMaxRelativeTolerance
5 | 2 | 0.095861 | SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.
emd(yBad,MaxNumIMF=5)

The next step in the analysis is to compute the Hilbert spectrum of the extracted IMFs. For more details, see the Compute Hilbert Spectrum of Vibration Signal (Signal Processing Toolbox) example.
Load and visualize a nonstationary continuous signal composed of sinusoidal waves with a distinct change in frequency. The vibration of a jackhammer and the sound of fireworks are examples of nonstationary continuous signals. The signal is sampled at a rate fs.
load("sinusoidalSignalExampleData.mat","X","fs") t = (0:length(X)-1)/fs; plot(t,X) xlabel("Time(s)")
The mixed signal contains sinusoidal waves with different amplitude and frequency values.
Perform empirical mode decomposition to plot the intrinsic mode functions and residual of the signal. Since the signal is not smooth, specify "pchip" as the interpolation method.
emd(X,Interpolation="pchip",Display=1)Current IMF | #Sift Iter | Relative Tol | Stop Criterion Hit
1 | 2 | 0.026352 | SiftMaxRelativeTolerance
2 | 2 | 0.0039573 | SiftMaxRelativeTolerance
3 | 1 | 0.024838 | SiftMaxRelativeTolerance
4 | 2 | 0.05929 | SiftMaxRelativeTolerance
5 | 2 | 0.11317 | SiftMaxRelativeTolerance
6 | 2 | 0.12599 | SiftMaxRelativeTolerance
7 | 2 | 0.13802 | SiftMaxRelativeTolerance
8 | 3 | 0.15937 | SiftMaxRelativeTolerance
9 | 2 | 0.15923 | SiftMaxRelativeTolerance
Decomposition stopped because the number of extrema in the residual signal is less than the 'MaxNumExtrema' value.

emd generates an interactive figure with the original signal, the first 3 IMFs, and the residual. The table generated in the command window indicates the number of sift iterations, the relative tolerance, and the sift stop criterion for each generated IMF. You can hide the table by removing the Display name-value argument or specifying it as 0.
Right-click on the white space in the figure to open the IMF selector window. Use IMF selector to selectively view the generated IMFs, the original signal, and the residual.

Select the IMFs to be displayed from the list. Choose whether to display the original signal and residual on the figure.

The selected IMFs are now displayed on the figure.

Use the figure to visualize individual components decomposed from the original signal along with the residual. Note that the residual is computed for the total number of IMFs, and does not change based on the IMFs selected in the IMF selector window.
Input Arguments
Time-domain signal, specified as a real-valued vector, or a
single-variable timetable with a single column. If x is
a timetable, x must contain increasing, finite row
times.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'MaxNumIMF',5
Cauchy-type convergence criterion, specified as the comma-separated
pair consisting of 'SiftRelativeTolerance' and a
positive scalar. SiftRelativeTolerance is one of the
sifting stop criteria, that is, sifting stops when the current relative
tolerance is less than SiftRelativeTolerance. For
more information, see Sift Relative Tolerance.
Maximum number of sifting iterations, specified as the comma-separated
pair consisting of 'SiftMaxIterations' and a positive
scalar integer. SiftMaxIterations is one of the
sifting stop criteria, that is, sifting stops when the current number of
iterations is larger than SiftMaxIterations.
SiftMaxIterations can be specified using only
positive whole numbers.
Maximum number of IMFs extracted, specified as the comma-separated
pair consisting of 'MaxNumIMF' and a positive scalar
integer. MaxNumIMF is one of the decomposition stop
criteria, that is, decomposition stops when number of IMFs generated is
equal to MaxNumIMF.
MaxNumIMF can be specified using only positive
whole numbers.
Maximum number of extrema in the residual signal, specified as the
comma-separated pair consisting of 'MaxNumExtrema'
and a positive scalar integer. MaxNumExtrema is one
of the decomposition stop criteria, that is, decomposition stops when
number of extrema is less than MaxNumExtrema.
MaxNumExtrema can be specified using only positive
whole numbers.
Signal to residual energy ratio, specified as the comma-separated pair
consisting of 'MaxEnergyRatio' and a scalar.
MaxEnergyRatio is the ratio of the energy of the
signal at the beginning of sifting and the average envelope energy.
MaxEnergyRatio is one of the decomposition stop
criteria, that is, decomposition stops when current energy ratio is
larger than MaxEnergyRatio. For more information, see
Energy Ratio.
Interpolation method for envelope construction, specified as the
comma-separated pair consisting of 'Interpolation'
and either 'spline' or
'pchip'.
Specify Interpolation as:
'spline', ifxis a smooth signal'pchip', ifxis a nonsmooth signal
'spline' interpolation method uses
cubic splines, while 'pchip' uses piecewise-cubic
Hermite interpolating polynomials.
Toggle information display in the command window, specified as the
comma-separated pair consisting of 'Display' and
either 0 or 1. The table generated in the command window indicates the
number of sift iterations, the relative tolerance, and the sift stop
criterion for each generated IMF. Specify Display as
1 to show the table or 0 to hide the table.
Output Arguments
Intrinsic mode function (IMF), returned as a matrix or timetable. Each IMF
is an amplitude and frequency modulated signal with positive and slowly
varying envelopes. To perform spectral analysis of a signal, you can apply
the Hilbert-Huang transform to its IMFs. See hht and Intrinsic Mode Functions.
imf is returned as:
A matrix whose each column is an
imf, whenxis a vectorA timetable, when
xis a single data column timetable
Residual of the signal, returned as a column vector or a single data
column timetable. residual represents the portion of the
original signal x not decomposed by
emd.
residual is returned as:
A column vector, when
xis a vector.A single data column timetable, when
xis a single data column timetable.
Additional information for diagnostics, returned as a structure with the following fields:
NumIMF— Number of IMFs extractedNumIMFis a vector from 1 to N, where N is the number of IMFs. If no IMFs are extracted,NumIMFis empty.NumExtrema— Number of extrema in each IMFNumExtremais a vector equal in length to the number of IMFs. The kth element ofNumExtremais the number of extrema found in the kth IMF. If no IMFs are extracted,NumExtremais empty.NumZerocrossing— Number of zero crossings in each IMFNumber of zero crossings in each IMF.
NumZerocrossingis a vector equal in length to the number of IMFs. The kth element ofNumZerocrossingis the number of zero crossings in the kth IMF. If no IMFs are extracted,NumZerocrossingis empty.NumSifting— Number of sifting iterations used to extract each IMFNumSiftingis a vector equal in length to the number of IMFs. The kth element ofNumSiftingis the number of sifting iterations used in the extraction of the kth IMF. If no IMFs are extracted,NumSiftingis empty.MeanEnvelopeEnergy— Energy of the mean of the upper and lower envelopes obtained for each IMFIf
UEis the upper envelope andLEis the lower envelope,MeanEnvelopeEnergyismean(((LE+UL)/2).^2).MeanEnvelopeEnergyis a vector equal in length to the number of IMFs. The kth element ofMeanEnvelopeEnergyis the mean envelope energy for the kth IMF. If no IMFs are extracted,MeanEnvelopeEnergyis empty.RelativeTolerance— Final relative tolerance of the residual for each IMFThe relative tolerance is defined as the ratio of the squared 2-norm of the difference between the residual from the previous sifting step and the residual from the current sifting step to the squared 2-norm of the residual from the ith sifting step. The sifting process stops when
RelativeToleranceis less thanSiftRelativeTolerance. For additional information, see Sift Relative Tolerance.RelativeToleranceis a vector equal in length to the number of IMFs. The kth element ofRelativeToleranceis the final relative tolerance obtained for the kth IMF. If no IMFs are extracted,RelativeToleranceis empty.
More About
The empirical mode decomposition (EMD) algorithm decomposes a signal x(t) into intrinsic mode functions (IMFs) and a residual in an iterative process. The core component of the algorithm involves sifting a function x(t) to obtain a new function Y(t):
First find the local minima and maxima of x(t).
Then use the local extrema to construct lower and upper envelopes s−(t) and s+(t), respectively, of x(t). Form the mean of the envelopes, m(t).
Subtract the mean from x(t) to obtain the residual: Y(t) = x(t) − m(t).
An overview of the decomposition is as follows:
To begin, let r0(t) = x(t), where x(t) is the initial signal, and let i = 0.
Before sifting, check ri(t):
Find the total number (TN) of local extrema of ri(t).
Find the energy ratio (ER) of ri(t) (see Energy Ratio).
If (ER >
MaxEnergyRatio) or (TN <MaxNumExtrema) or (number of IMFs >MaxNumIMF) then stop the decomposition.Let ri,Prev(t) = ri(t).
Sift ri,Prev(t) to obtain ri,Cur(t).
Check ri,Cur(t)
Find the relative tolerance (RT) of ri,Cur(t) (see Sift Relative Tolerance).
Get current sift iteration number (IN).
If (RT <
SiftRelativeTolerance) or (IN >SiftMaxIterations) then stop sifting. An IMF has been found: IMFi(t) = ri,Cur(t). Otherwise, let ri,Prev(t) = ri,Cur(t) and go to Step 5.Let ri+1(t) = ri(t) − ri,Cur(t).
Let i = i + 1. Return to Step 2.
The EMD algorithm decomposes, via an iterative sifting process, a signal x(t) into IMFs imfi(t) and a residual rN(t):
When first introduced by Huang et al. [1], an IMF was defined to be a function with two characteristics:
The number of local extrema — the total number of local minima and local maxima — and the number of zero crossings differ by at most one.
The mean value of the upper and lower envelopes constructed from the local extrema is zero.
However, as noted in [4], sifting until a strict IMF is obtained can result in IMFs that have no physical significance. Specifically, sifting until the number of zero crossings and local extrema differ by at most one can result in pure-tone like IMFs, in other words, functions very similar to what would be obtained by projection on the Fourier basis. This situation is precisely what EMD strives to avoid, preferring AM-FM modulated components for their physical significance.
Reference [4] proposes options to
obtain physically meaningful results. The emd function relaxes
the original IMF definition by using Sift Relative Tolerance, a Cauchy-type stop
criterion. The emd function iterates to extract natural AM-FM
modes. The IMFs generated may fail to satisfy the local extrema-zero crossings
criteria. See Zero Crossings and Extrema in Intrinsic Mode Function of Sinusoid.
Sift Relative Tolerance is a Cauchy-type
stop criterion proposed in [4]. Sifting stops when
current relative tolerance is less than SiftRelativeTolerance.
The current relative tolerance is defined as
Because the Cauchy criterion does not directly count the number
of zero crossings and local extrema, it is possible that the IMFs returned by the
decomposition do not satisfy the strict definition of an intrinsic mode function. In
those cases, you can try reducing the value of the
SiftRelativeTolerance from its default value. See [4] for a detailed
discussion of stopping criteria. The reference also discusses the advantages and
disadvantages of insisting on strictly defined IMFs in empirical mode
decomposition.
Energy ratio is the ratio of the energy of the signal at the
beginning of sifting and the average envelope energy [2]. Decomposition stops
when current energy ratio is larger than MaxEnergyRatio. For
the ith IMF, the energy ratio is defined as
References
[1] Huang, Norden E., Zheng Shen, Steven R. Long, Manli C. Wu, Hsing H. Shih, Quanan Zheng, Nai-Chyuan Yen, Chi Chao Tung, and Henry H. Liu. “The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis.” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 454, no. 1971 (March 8, 1998): 903–95. https://doi.org/10.1098/rspa.1998.0193.
[2] Rato, R.T., M.D. Ortigueira, and A.G. Batista. “On the HHT, Its Problems, and Some Solutions.” Mechanical Systems and Signal Processing 22, no. 6 (August 2008): 1374–94. https://doi.org/10.1016/j.ymssp.2007.11.028.
[3] Rilling, Gabriel, Patrick Flandrin, and Paulo Gonçalves. "On Empirical Mode Decomposition and Its Algorithms." IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing 2003. NSIP-03. Grado, Italy. 8–11.
[4] Wang, Gang, Xian-Yao Chen, Fang-Li Qiao, Zhaohua Wu, and Norden E. Huang. “On Intrinsic Mode Function.” Advances in Adaptive Data Analysis 02, no. 03 (July 2010): 277–93. https://doi.org/10.1142/S1793536910000549.
Extended Capabilities
Usage notes and limitations:
Timetables are not supported for code generation.
If supplied, the interpolation method specified using the
'Interpolation'name-value pair must be a compile-time constant.
Version History
Introduced in R2018a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)