dwt
Single-level 1-D discrete wavelet transform
Description
[
returns the single-level discrete wavelet transform (DWT) of the vector cA,cD] = dwt(x,wname)x
using the wavelet specified by wname. The wavelet must be recognized by
wavemngr. dwt returns the approximation coefficients vector
cA and detail coefficients vector cD of the DWT.
Note
If your application requires a multilevel wavelet decomposition, consider using wavedec.
[
returns the single-level DWT with the specified extension mode cA,cD] = dwt(___,"mode",extmode)extmode. For
more information, see dwtmode. This argument can be added to any of
the previous input syntaxes.
Note
For gpuArray inputs, the supported modes are "symh"
("sym") and "per". All "mode"
options except "per" are converted to "symh". See the
example Single-Level Discrete Wavelet Transform on GPU.
Examples
Input Arguments
Output Arguments
Algorithms
Starting from a signal s of length N, two sets of
coefficients are computed: approximation coefficients
cA1, and detail coefficients
cD1. Convolving s with the scaling
filter LoD, followed by dyadic decimation, yields the approximation
coefficients. Similarly, convolving s with the wavelet filter
HiD, followed by dyadic decimation, yields the detail coefficients.
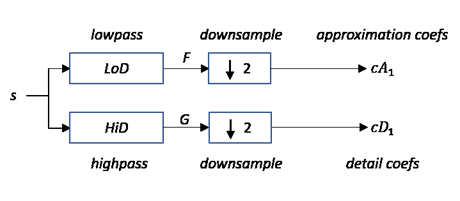
where
 — Convolve with filter X
— Convolve with filter X— Downsample (keep the even-indexed elements)
The length of each filter is equal to 2n. If N = length(s), the signals F and G are of length N + 2n −1 and the coefficients cA1 and cD1 are of length floor.
To deal with signal-end effects resulting from a convolution-based algorithm, a global
variable managed by dwtmode defines the kind of signal extension mode
used. The possible options include zero-padding and symmetric extension, which is the default
mode.
Note
For the same input, the dwt function and the DWT block in the
DSP System Toolbox™ do not produce the same results. The DWT block is designed for real-time
implementation while Wavelet Toolbox™ software is designed for analysis, so the products handle boundary conditions and
filter states differently.
To make the dwt function output match the DWT block output, set the
function boundary condition to zero-padding by typing dwtmode("zpd") at the
MATLAB® command prompt. To match the latency of the DWT block, which is implemented using
FIR filters, add zeros to the input of the dwt function. The number of
zeros you add must be equal to half the filter length.
References
[1] Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S. G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 11, Issue 7, July 1989, pp. 674–693.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.
Extended Capabilities
Version History
Introduced before R2006a
See Also
wavedec | idwt | dwtmode | waveinfo | dwtfilterbank