pdeCoefficients
Description
coeffs = pdeCoefficients(pdeeq,u)specifyCoefficients function in Partial Differential Equation Toolbox™.
pdeeq is a scalar PDE or a PDE system in symbolic form that is a
function of u. The pdeCoefficients function converts
pdeeq into a system of equations of the form
and returns the structure coeffs that contains the
coefficients m, d, c,
a, and f. For more information, see Equations You Can Solve Using Partial Differential Equation Toolbox (Partial Differential Equation Toolbox).
If pdeCoefficients cannot convert a PDE into the divergence form
above, then it issues a warning message and writes all remaining gradients to the
f coefficient. Partial Differential Equation Toolbox will be unable to solve this type of PDE.
Examples
Create a symbolic PDE that represents the Laplacian of the variable u(x,y).
syms u(x,y)
pdeeq = laplacian(u,[x y]) == -3pdeeq(x, y) =
Extract the coefficients of the PDE.
coeffs = pdeCoefficients(pdeeq,u)
coeffs = struct with fields:
a: 0
c: [4×1 double]
m: 0
d: 0
f: -3
pdeCoefficients converts the symbolic PDE into a scalar PDE equation of the form
and extracts the coefficients m, d, c, a, and f into the structure coeffs. For 2-D systems of equations, c is a tensor with 4 elements. For more information, see c Coefficient for specifyCoefficients (Partial Differential Equation Toolbox). In this case, , so the coefficient c is a 4-by-1 column vector that represents c, c, c, and c.
coeffs.c
ans = 4×1
-1
0
0
-1
Solve a 2-D homogenous Laplace's equation in the domain bounded by a unit circle. Use the pdeCoefficients function to extract the coefficients of the Laplace's equation.
Create the PDE model and include the geometry.
model = createpde; geometryFromEdges(model,@circleg);
Plot the geometry and display the edge labels for use in the boundary condition definition.
figure pdegplot(model,'EdgeLabels','on') axis equal

Create a symbolic expression pdeeq that represents the Laplace's equation.
syms u(x,y)
pdeeq = laplacian(u,[x y])pdeeq(x, y) =
Extract the coefficients of the Laplace's equation.
coeffs = pdeCoefficients(pdeeq,u)
coeffs = struct with fields:
a: 0
c: [4×1 double]
m: 0
d: 0
f: 0
Specify the coefficients of the PDE model.
specifyCoefficients(model,'m',coeffs.m,'d',coeffs.d, ... 'c',coeffs.c,'a',coeffs.a,'f',coeffs.f);
Apply the Dirichlet boundary condition at all 4 edges that form the circle.
applyBoundaryCondition(model,'dirichlet','Edge',1:4,'u',@(region,state) region.x.^4 + region.y.^4);
Generate the default mesh for the geometry.
generateMesh(model);
Solve the PDE and plot the solution.
results = solvepde(model);
pdeplot(model,'XYData',results.NodalSolution)
Solve a 2-D Poisson's equation in the domain bounded by a unit circle. The divergence form of the PDE has nonconstant f coefficient. You can solve the PDE by extracting the coefficients using pdeCoefficients and specifying the coefficients in the PDE model using specifyCoefficients.
Create the PDE model and include the geometry.
model = createpde; geometryFromEdges(model,@circleg);
Create a symbolic expression pdeeq that represents Poisson's equation.
syms u(x,y)
pdeeq = diff(u,x,x) + diff(u,y,y) - 1/(x^2 + y^2)pdeeq(x, y) =
Extract the coefficients of the equation.
coeffs = pdeCoefficients(pdeeq,u)
coeffs = struct with fields:
a: 0
c: [4×1 double]
m: 0
d: 0
f: @makeCoefficient/coefficientFunction
The f coefficient is not a constant. It is displayed as @makeCoefficient/coefficientFunction, which indicates that it has been returned from the workspace of some internal function. To show the formula behind the function handle, use coeffs.f('show').
coeffs.f('show')ans =
Specify the coefficients of the PDE model.
specifyCoefficients(model,'m',coeffs.m,'d',coeffs.d, ... 'c',coeffs.c,'a',coeffs.a,'f',coeffs.f);
Apply the Dirichlet boundary condition at all 4 edges that form the circle.
applyBoundaryCondition(model,'dirichlet','Edge',1:4,'u',0);
Generate the default mesh for the geometry.
generateMesh(model);
Solve the PDE. Plot the nodal solution using the option 'XYData' in the pdeplot function.
results = solvepde(model);
pdeplot(model,'XYData',results.NodalSolution)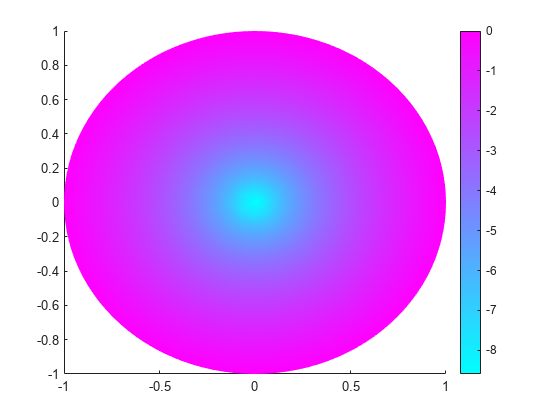
Plot the gradient of the solution at the nodal locations using the option 'FlowData'.
pdeplot(model,'FlowData',[results.XGradients results.YGradients])
Construct a PDE with no divergence form.
syms u(x,y)
pdeeq = diff(u,x,x) + cos(x+y)/4*diff(u,x,y) + 1/2*diff(u,y,y)pdeeq(x, y) =
Extract its coefficients. When pdeCoefficients cannot convert a PDE into the divergence form
,
it issues a warning message, but it still produces output.
coeffs = pdeCoefficients(pdeeq,u)
Warning: After extracting m, d, and c, some gradients remain. Writing all remaining terms to f.
coeffs = struct with fields:
a: 0
c: @makeCoefficient/coefficientFunction
m: 0
d: 0
f: @makeCoefficient/coefficientFunction
To show the function handles in the extracted coefficients c and f, use the option 'show'. All remaining gradients in the PDE are written to the f coefficient.
coeffs.c('show')ans =
coeffs.f('show')ans =
Since the PDE has no divergence form required by the PDE Toolbox, the toolbox will be unable to solve this PDE.
Solve a time-dependent wave equation in the domain bounded by a unit circle. The wave equation is a PDE with a scalar function that depends on time and coordinates and .
Create the PDE model and include the geometry.
model = createpde(1); geometryFromEdges(model,@circleg);
Create a symbolic PDE that represents the wave equation.
syms u(t,x,y)
pdeeq = diff(u,t,t) - laplacian(u,[x y])pdeeq(t, x, y) =
Extract the coefficients of the PDE.
coeffs = pdeCoefficients(pdeeq,u)
coeffs = struct with fields:
a: 0
c: [4×1 double]
m: 1
d: 0
f: 0
Specify the coefficients of the PDE model.
specifyCoefficients(model,'m',coeffs.m,'d',coeffs.d, ... 'c',coeffs.c,'a',coeffs.a,'f',coeffs.f);
Set the initial conditions of the time-dependent problem on the entire geometry.
setInitialConditions(model,0,1);
Apply the Dirichlet boundary condition at all 4 edges that form the circle.
applyBoundaryCondition(model,'dirichlet','Edge',1:4,'u',0);
Generate the default mesh for the geometry.
generateMesh(model);
Find the solutions of the time-dependent PDE at a time range from 0s to 50s with a 2s interval.
results = solvepde(model,linspace(0,2,50));
Plot the solution of the wave equation for each 5s interval.
figure; for k = 1:10 subplot(5,2,k); pdeplot(model,'XYData',results.NodalSolution(:,k*5)) axis equal end

Solve a system of two second-order PDEs. You can solve the PDE system by extracting the PDE coefficients symbolically using pdeCoefficients, converting the coefficients to double-precision numbers using pdeCoefficientsToDouble, and specifying the coefficients in the PDE model using specifyCoefficients.
The system of PDEs represents the deflection of a clamped structural plate under a uniform pressure load. The system of PDEs with the dependent variables and is given by
,
,
where is the bending stiffness of the plate given by
,
and is the modulus of elasticity, is Poisson's ratio, is the plate thickness, is the transverse deflection of the plate, and is the pressure load.
Create a PDE model for the system of two equations.
model = createpde(2);
Create a square geometry. Specify the side length of the square. Then include the geometry in the PDE model.
len = 10.0; gdm = [3 4 0 len len 0 0 0 len len]'; g = decsg(gdm,'S1',('S1')'); geometryFromEdges(model,g);
Specify the values of the physical parameters of the system. Let the external pressure be a symbolic variable pres that can take any value.
E = 1.0e6;
h_thick = 0.1;
nu = 0.3;
D = E*h_thick^3/(12*(1 - nu^2));
syms presDeclare the PDE system as a system symbolic equations. Extract the coefficients of the PDE and return them in symbolic form.
syms u1(x,y) u2(x,y) pdeeq = [-laplacian(u1) + u2; -D*laplacian(u2) - pres]; symCoeffs = pdeCoefficients(pdeeq,[u1 u2],'Symbolic',true)
symCoeffs = struct with fields:
m: 0
a: [2×2 sym]
c: [4×4 sym]
f: [2×1 sym]
d: 0
Display the coefficients m, a, c, f, and d.
structfun(@disp,symCoeffs)
Substitute a value for pres using the subs function. Since the outputs of subs are symbolic objects, use the pdeCoefficientsToDouble function to convert the coefficients to the double data type, which makes them valid inputs for the Partial Differential Equation Toolbox.
symCoeffs = subs(symCoeffs,pres,2); coeffs = pdeCoefficientsToDouble(symCoeffs)
coeffs = struct with fields:
a: [4×1 double]
c: [16×1 double]
m: 0
d: 0
f: [2×1 double]
Specify the PDE coefficients for the PDE model.
specifyCoefficients(model,'m',coeffs.m,'d',coeffs.d, ... 'c',coeffs.c,'a',coeffs.a,'f',coeffs.f);
Specify spring stiffness. Specify boundary conditions by defining distributed springs on all four edges.
k = 1e7; bOuter = applyBoundaryCondition(model,'neumann','Edge',(1:4), ... 'g',[0 0],'q',[0 0; k 0]);
Specify the mesh size of the geometry and generate a mesh for the PDE model.
hmax = len/20;
generateMesh(model,'Hmax',hmax);Solve the model.
res = solvepde(model);
Access the solution at the nodal locations.
u = res.NodalSolution;
Plot the transverse deflection of the plate.
numNodes = size(model.Mesh.Nodes,2); figure; pdeplot(model,'XYData',u(1:numNodes),'contour','on') title 'Transverse Deflection'
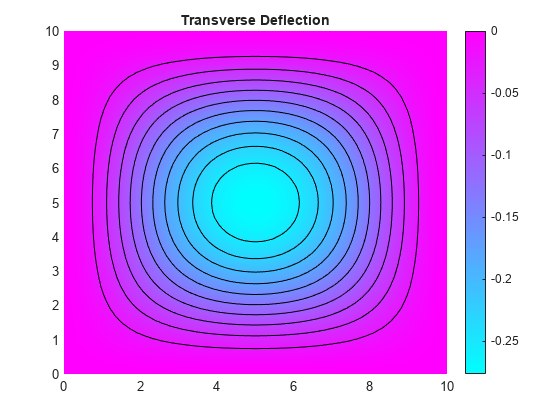
Find the transverse deflection at the plate center.
wMax = min(u(1:numNodes,1))
wMax = -0.2763
Compare the result with the deflection at the plate center computed analytically.
pres = 2; wMax = -.0138*pres*len^4/(E*h_thick^3)
wMax = -0.2760
Input Arguments
PDE in symbolic form, specified as a symbolic equation, expression, or a symbolic vector.
Dependent variables of PDE, specified as a symbolic function. u
must contain stationary or time-dependent variables in two or three dimensions. For
example, create the variable u using one of these statements:
syms u(x,y)syms u(t,x,y)syms u(x,y,z)syms u(t,x,y,z)
Output Arguments
Coefficients of PDE operating on doubles, returned as a structure of
double-precision numbers and function handles as required by the
specifyCoefficients function. The fields of the structure are
a, c, m,
d, and f. For details on interpreting the
coefficients in the format required by Partial Differential Equation Toolbox, see:
c Coefficient for specifyCoefficients (Partial Differential Equation Toolbox)
m, d, or a Coefficient for specifyCoefficients (Partial Differential Equation Toolbox)
f Coefficient for specifyCoefficients (Partial Differential Equation Toolbox)
When pdeCoefficients returns a coefficient as a function handle,
the function handle takes two structures as input arguments, location
and state, and returns double-precision output. The function handle
is displayed as @makeCoefficient/coefficientFunction in the Command
Window. To display the formula of the function handle in coeffs.f in
symbolic form, use coeffs.f('show').
In some cases, not all generated coefficients can be used by
specifyCoefficients. For example, the d
coefficient must take a special matrix form when m is nonzero. For
more details, see d Coefficient When m Is Nonzero (Partial Differential Equation Toolbox).
Coefficients of PDE in symbolic form, returned as a structure of symbolic expressions.
Version History
Introduced in R2021a
See Also
syms | diff | laplacian | pdeCoefficientsToDouble | specifyCoefficients (Partial Differential Equation Toolbox)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)