Applications
Symbolic Math Toolbox provides tools to solve, plot, and manipulate mathematical expressions, both analytically and numerically with high precision. From the results of symbolic computations, you can also generate MATLAB® functions, Simulink® Function blocks, and Simscape™ equations to use with other toolboxes. Use these tools to perform application-specific workflows.
Teaching and Research
Mathematics
- Eigenvalues of the Laplace Operator
This example shows how to solve the eigenvalue problem of the Laplace operator on an L-shaped region. - Solve Partial Differential Equation of Nonlinear Heat Transfer
This example shows how to solve a partial differential equation (PDE) of nonlinear heat transfer in a thin plate. - Solve Partial Differential Equation of Tsunami Model
This example simulates a tsunami wave phenomenon by solving the partial differential equations that model the tsunami. - Using Symbolic Mathematics with Optimization Toolbox Solvers
This example shows how to use the Symbolic Math Toolbox functionsjacobianandmatlabFunctionto provide analytical derivatives to optimization solvers. - Analytical Plotting with Symbolic Math Toolbox
Symbolic Math Toolbox provides analytical plotting of mathematical expressions without explicitly generating numerical data.
Physics
- The Physics of the Damped Harmonic Oscillator
This example explores the physics of the damped harmonic oscillator by solving the equations of motion in the case of no driving forces. - Simulate the Motion of the Periodic Swing of a Pendulum
Solve the equation of motion of a simple pendulum analytically for small angles and numerically for any angle. - Functional Derivatives Tutorial
This example shows how to use functional derivatives in Symbolic Math Toolbox using the context of a wave equation. - Solve Differential Equations of RLC Circuit Using Laplace Transform
Solve differential equations of an RLC circuit by using Laplace and inverse Laplace transforms. - Harmonic Analysis of Transfer Function Output
This example finds closed-form solutions for the coefficients of frequencies in an output signal. - Units in Physics Calculations
This example shows how to work with units in physics calculations.
Mathematical System Modeling
Animation and Model of Automotive Piston
This example shows how to model the motion of an automotive piston by using MATLAB and Symbolic Math Toolbox.
Padé Approximant of Time-Delay Input
This example shows how to use a Padé approximant in control system theory to model time delays in the response of a first-order system.
Analytical Model of Cantilever Truss Structure for Simscape
This example shows how to find parameterized analytical expressions for the displacement of a joint of a cantilever truss structure in both the static and frequency domains.
Estimate Model Parameters of a Symbolically Derived Plant Model in Simulink
This example uses Simulink Design Optimization to estimate the unknown capacitance and initial voltage of a symbolically derived algebraic model of a simple resistor-capacitor (RC) circuit.
Customize and Extend Simscape Libraries for a Custom DC Motor
Create custom-equation-based components for the Simscape library using Symbolic Math Toolbox.
Finite Element Formulation for Timoshenko Beam Problem
This example shows how to apply the finite element method (FEM) to solve a Timoshenko beam problem, using both linear and quadratic basis functions for analysis.
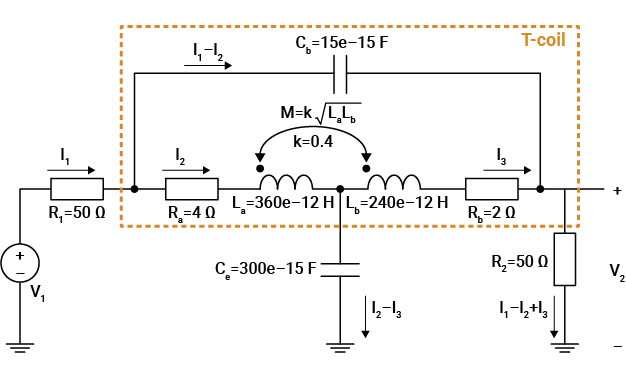
Analyze Transfer Function of T-Coil Circuit
This example shows how to analyze the transfer function of a T-coil circuit using Symbolic Math Toolbox™ and Control System Toolbox™.
Robotic Control Systems
Analytical Solutions of the Inverse Kinematics of a Humanoid Robot
This example shows how to derive analytical solutions for the inverse kinematics of the head chain of a humanoid robot.
Derive and Apply Inverse Kinematics to Two-Link Robot Arm
This example shows how to derive and apply inverse kinematics to a two-link robot arm by using MATLAB and Symbolic Math Toolbox.
Derive Quadrotor Dynamics for Nonlinear Model Predictive Control
This example shows how to derive a continuous-time nonlinear model of a quadrotor using Symbolic Math Toolbox.
Derive Equations of Motion and Simulate Cart-Pole System
This example shows how to derive the equations of motion for the cart-pole system using Symbolic Math Toolbox™ and then simulate the cart-pole system using the ode45 solver.
Quantitative Finance
The Black–Scholes Formula for Call Option Price
This example shows how to calculate the call option price using the Black–Scholes formula.
Explore Single-Period Asset Arbitrage
Explore basic arbitrage concepts in a single-period, two-state asset portfolio.
Simulate a Stochastic Process Using the Feynman–Kac Formula
This example obtains the partial differential equation that describes the expected final price of an asset whose price is a stochastic process given by a stochastic differential equation.
Markov Chain Analysis and Stationary Distribution
This example shows how to derive the symbolic stationary distribution of a trivial Markov chain by computing its eigen decomposition.
Related Information
Featured Examples
Solve Partial Differential Equation of Nonlinear Heat Transfer
Solve a partial differential equation (PDE) of nonlinear heat transfer in a thin plate.
Analytical Plotting with Symbolic Math Toolbox
Symbolic Math Toolbox provides analytical plotting of mathematical expressions without explicitly generating numerical data.
Simulate the Motion of the Periodic Swing of a Pendulum
Solve the equation of motion of a simple pendulum analytically for small angles and numerically for any angle.
Analytical Model of Cantilever Truss Structure for Simscape
Find parameterized analytical expressions for the displacement of a joint of a cantilever truss structure in both the static and frequency domains.
Analyze Transfer Function of T-Coil Circuit
Analyze the transfer function of a T-coil circuit using Symbolic Math Toolbox™ and Control System Toolbox™. In this example, you define symbolic equations, solve for the transfer function, and analyze the stability, frequency response, and step response of the circuit.
Derive and Apply Inverse Kinematics to Two-Link Robot Arm
Derive and apply inverse kinematics to a two-link robot arm by using MATLAB and Symbolic Math Toolbox.
Explore Single-Period Asset Arbitrage
Explore basic arbitrage concepts in a single-period, two-state asset portfolio.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)