Derive and Apply Inverse Kinematics to Two-Link Robot Arm
This example shows how to derive and apply inverse kinematics to a two-link robot arm by using MATLAB® and Symbolic Math Toolbox™.
The example defines the joint parameters and end-effector locations symbolically, calculates and visualizes the forward and inverse kinematics solutions, and finds the system Jacobian, which is useful for simulating the motion of the robot arm.

Step 1: Define Geometric Parameters
Define the link lengths, joint angles and end-effector locations of the robots as symbolic variables.
syms L_1 L_2 theta_1 theta_2 XE YE
Specify values for the link lengths of the robot.
L1 = 1; L2 = 0.5;
Step 2: Define X and Y Coordinates of End Effector

Define the X and Y coordinates of the end-effector as a function of the joint angles .
XE_RHS = L_1*cos(theta_1) + L_2*cos(theta_1+theta_2)
XE_RHS =
YE_RHS = L_1*sin(theta_1) + L_2*sin(theta_1+theta_2)
YE_RHS =
Convert the symbolic expressions into MATLAB functions.
XE_MLF = matlabFunction(XE_RHS,Vars=[L_1 L_2 theta_1 theta_2]); YE_MLF = matlabFunction(YE_RHS,Vars=[L_1 L_2 theta_1 theta_2]);
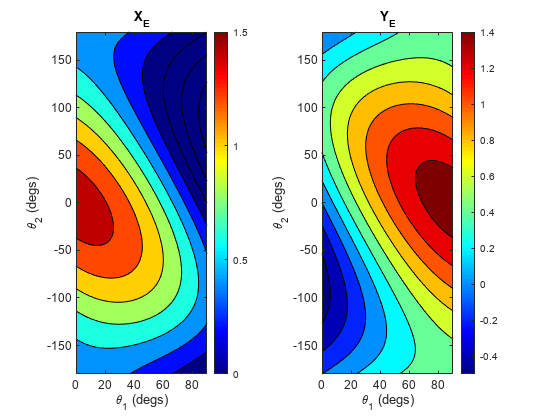
Step 3: Calculate and Visualize Forward Kinematics
Forward kinematics transforms the joint angles into end-effector locations: . Given specific joint-angle values, use forward kinematics to calculate the end-effector locations.
Specify the input values of the joint angles as and .
t1_degs_row = linspace(0,90,100); t2_degs_row = linspace(-180,180,100); [tt1_degs,tt2_degs] = meshgrid(t1_degs_row,t2_degs_row);
Convert the angle units from degrees to radians.
tt1_rads = deg2rad(tt1_degs); tt2_rads = deg2rad(tt2_degs);
Calculate the X and Y coordinates using the MATLAB functions XE_MLF and YE_MLF, respectively.
X_mat = XE_MLF(L1,L2,tt1_rads,tt2_rads); Y_mat = YE_MLF(L1,L2,tt1_rads,tt2_rads);
Visualize the X and Y coordinates using the helper function plot_XY_given_theta_2dof.
plot_XY_given_theta_2dof(tt1_degs,tt2_degs,X_mat,Y_mat,(L1+L2))
Step 4: Find Inverse Kinematics
Inverse kinematics transforms the end-effector locations into joint angles: . Find the inverse kinematics from the forward kinematics equations.
Define the forward kinematics equations.
XE_EQ = XE == XE_RHS; YE_EQ = YE == YE_RHS;
Solve for and .
S = solve([XE_EQ YE_EQ],[theta_1 theta_2])
S = struct with fields:
theta_1: [2×1 sym]
theta_2: [2×1 sym]
The structure S represents the multiple solutions for and . Show the pair of solutions for .
simplify(S.theta_1)
ans =
Show the pair of solutions for .
simplify(S.theta_2)
ans =
Convert the solutions into MATLAB functions that you can use later. The functions TH1_MLF and TH2_MLF represent the inverse kinematics.
TH1_MLF{1} = matlabFunction(S.theta_1(1),Vars=[L_1 L_2 XE YE]);
TH1_MLF{2} = matlabFunction(S.theta_1(2),Vars=[L_1 L_2 XE YE]);
TH2_MLF{1} = matlabFunction(S.theta_2(1),Vars=[L_1 L_2 XE YE]);
TH2_MLF{2} = matlabFunction(S.theta_2(2),Vars=[L_1 L_2 XE YE]);Step 5: Calculate and Visualize Inverse Kinematics
Use the inverse kinematics to compute and from the X and Y coordinates.
Define the grid points of the X and Y coordinates.
[xmat,ymat] = meshgrid(0:0.01:1.5,0:0.01:1.5);
Calculate the angles and using the MATLAB functions TH1_MLF{1} and TH2_MLF{1}, respectively.
tmp_th1_mat = TH1_MLF{1}(L1,L2,xmat,ymat);
tmp_th2_mat = TH2_MLF{1}(L1,L2,xmat,ymat);Convert the angle units from radians to degrees.
tmp_th1_mat = rad2deg(tmp_th1_mat); tmp_th2_mat = rad2deg(tmp_th2_mat);
Some of the input coordinates, such as (X,Y) = (1.5,1.5), are beyond the reachable workspace of the end effector. The inverse kinematics solutions can generate some imaginary theta values that require correction. Correct the imaginary theta values.
th1_mat = NaN(size(tmp_th1_mat)); th2_mat = NaN(size(tmp_th2_mat)); tf_mat = imag(tmp_th1_mat) == 0; th1_mat(tf_mat) = real(tmp_th1_mat(tf_mat)); tf_mat = imag(tmp_th2_mat) == 0; th2_mat(tf_mat) = real(tmp_th2_mat(tf_mat));
Visualize the angles and using the helper function plot_theta_given_XY_2dof.
plot_theta_given_XY_2dof(xmat,ymat,th1_mat,th2_mat)

Step 6: Compute System Jacobian
The definition of the system Jacobian is:
the_J = jacobian([XE_RHS YE_RHS],[theta_1 theta_2])
the_J =
You can relate the joint velocity to the end-effector velocity and the other way around, by using the system Jacobian and its Moore-Penrose pseudoinverse :
You can also convert the symbolic expression of the Jacobian to a MATLAB function block. Simulate the end-effector locations of the robot on a trajectory by defining the multiple waypoints as inputs to a Simulink® model. The Simulink model can calculate a motion-profile based on the joint angle values to reach each waypoint in the trajectory. For more details, see Inverse Kinematics of a 2-link Robot Arm and Teaching Rigid Body Dynamics.
Helper Functions
function plot_theta_given_XY_2dof(X_mat,Y_mat,theta_1_mat_degs,... theta_2_mat_degs) xlab_str = "X (m)"; ylab_str = "Y (m)"; figure; hax(1) = subplot(1,2,1); contourf(X_mat,Y_mat,theta_1_mat_degs); clim(hax(1),[-180 180]); colormap(gca,"jet"); colorbar xlabel(xlab_str,Interpreter="tex"); ylabel(ylab_str,Interpreter="tex"); title(hax(1),"\theta_1",Interpreter="tex") axis("equal") hax(2) = subplot(1,2,2); contourf(X_mat,Y_mat,theta_2_mat_degs); clim(hax(2),[-180 180]); colormap(gca,"jet"); colorbar xlabel(xlab_str,Interpreter="tex"); ylabel(ylab_str,Interpreter="tex"); title(hax(2),"\theta_2",Interpreter="tex") axis("equal") end function plot_XY_given_theta_2dof(theta_1_mat_degs,theta_2_mat_degs,... X_mat,Y_mat,a_cmax) xlab_str = "\theta_1 (degs)"; ylab_str = "\theta_2 (degs)"; figure; hax(1) = subplot(1,2,1); contourf(theta_1_mat_degs,theta_2_mat_degs,X_mat); clim(hax(1),[0 a_cmax]); colormap(gca,"jet"); colorbar xlabel(xlab_str,Interpreter="tex"); ylabel(ylab_str,Interpreter="tex"); title(hax(1),"X_E",Interpreter="tex") hax(2) = subplot(1,2,2); contourf(theta_1_mat_degs,theta_2_mat_degs,Y_mat); clim(hax(1),[0 a_cmax]); colormap(gca,"jet"); colorbar xlabel(xlab_str,Interpreter="tex"); ylabel(ylab_str,Interpreter="tex"); title(hax(2),"Y_E",Interpreter="tex") end
See Also
Functions
matlabFunction|solve|simplify|jacobian