power_lineparam
(To be removed) Compute RLC parameters of overhead transmission line from its conductor characteristics and tower geometry
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Syntax
Description
DATA = power_lineparam('MYLINEDATA')'MYLINEDATA' is the name of a MAT-file. The MAT-file must
contain a structure variable of the same format as the DATA
variable.
power_lineparam(
uploads the RLC line parameters in the specified PI Section Line, PI Section Cable,
Distributed Parameters Line, or Three-Phase PI Section Line block.
DATA, 'BLK')'BLK' is a block path name. You can also specify a file name
for DATA.
Input Arguments
Output Arguments
Algorithms
The power_lineparam function computes the resistance, inductance,
and capacitance matrices of an arbitrary arrangement of conductors of an overhead
transmission line. For a three-phase line, the symmetrical component RLC values are also
computed.
The following figure shows a typical conductor arrangement for a three-phase
double-circuit line. This line configuration illustrates the various line parameters you
specify in the DATA structure.
Configuration of a Three-Phase Double-Circuit Line

For a set of N conductors, power_lineparam computes three
N-by-N matrices: the series resistance and
inductance matrices [R] and [L] and the shunt capacitance matrix [C]. These matrices are
required by the Distributed Parameters Line block for modeling
N-phase asymmetrical lines and by the single-phase PI Section
Line block. power_lineparam also computes the symmetrical component
RLC parameters required by the Three-Phase PI Section Line block. For two coupled
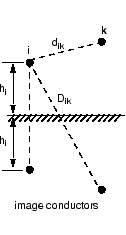
conductors, i and k, the self and mutual terms of the R, L, and C matrices are computed
using the concept of image conductors [1].
The self and mutual resistance terms are:
The self and mutual inductance terms are:
The self and mutual potential coefficients terms are:
where:
µ0 is the permeability of free space = 4π.10−4 H/km
ɛ0 is the permittivity of free space = 8.8542.10−9 F/km
ri is the radius of conductor i in meters
dik is the distance between conductors i and k, in meters
Dik is the distance between conductor i and image of k, in meters
hi is the average height of conductor i above ground, in meters
Rint, Lint are the internal resistance and inductance of conductor
ΔRii, ΔRik are the Carson R correction terms due to ground resistivity
ΔLii, ΔLik are the Carson L correction terms due to ground resistivity
The conductor self-inductance is computed from the magnetic flux circulating inside and outside the conductor, and produced by the current flowing in the conductor itself. The part of flux circulating inside the conducting material contributes to the internal inductance Lint, which is dependent on the conductor geometry. Assuming a hollow or solid conductor, the internal inductance is computed from the T/D ratio, where D is the conductor diameter and T is the thickness of the conducting material. See the figure Configuration of a Three-Phase Double-Circuit Line. The conductor self-inductance is computed by means of modified Bessel functions from the conductor diameter, T/D ratio, resistivity, and relative permeability of conducting material and specified frequency [1].
The conductor self-inductance can also be computed from parameters that are usually found in tables provided by conductor manufacturers: the Geometric Mean Radius (GMR) or the "Reactance at one-foot spacing."
The GMR is the radius of the equivalent hollow conductor with zero thickness, producing no internal flux, giving the same self-inductance. The conductor self-inductance is then derived from the GMR using the following equation:
For a solid conductor (T/D=0.5), the GMR is
| r = radius of conductor |
| μr = relative permeability of conducting material |
The GMR obtained from this equation assumes a uniform current density in the conductor. This assumption is strictly valid in DC. In AC, the GMR is slightly higher. For example, for a 3 cm diameter solid aluminum conductor (Rdc = 0.040 Ω/km), the GMR increases from 1.1682 cm in DC to 1.1784 cm at 60 Hz. Manufacturers usually give the GMR at the system nominal frequency (50 Hz or 60 Hz).
The reactance Xa at 1-foot spacing (or 1-meter spacing, if metric units are used) is the positive-sequence reactance of a three-phase line having one foot (or one meter) spacing between the three phases and infinite conductor heights. The reactance at 1-foot spacing (or 1-meter spacing) at frequency f is related to the GMR by the following equation:
| GMR = Geometric Mean Radius in feet or meters |
| ω = 2π.f in rad/s |
| f = frequency in hertz |
The conductor resistance matrix at a particular frequency depends on the DC resistance
of the conductor corrected for skin effect and ground resistivity. Both the resistance
matrix and the inductance matrix are dependent on the ground resistivity and frequency.
Correction terms for the R and L terms as developed by J.R. Carson in 1926 [2] are
implemented in power_lineparam.
References
[1] Dommel, H., et al., Electromagnetic Transients Program Reference Manual (EMTP Theory Book), 1986.
[2] Carson, J. R., "Wave Propagation in Overhead Wires with Ground Return," Bell Systems Technical Journal, Vol. 5, pp 539-554, 1926.