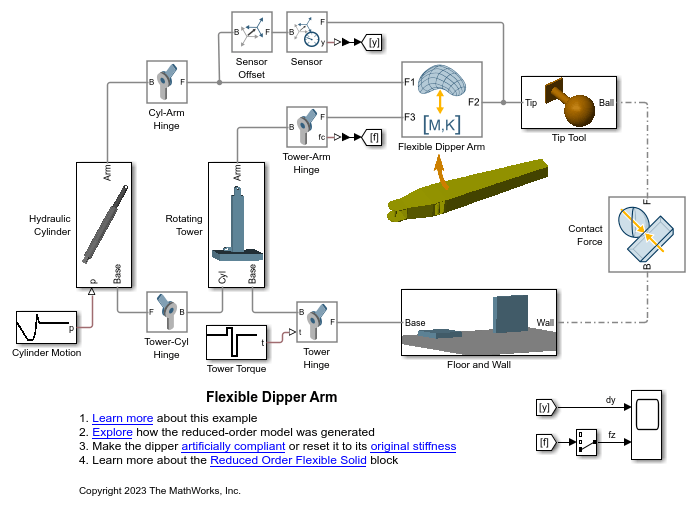
Reduced Order Flexible Solid

Flexible body based on a reduced-order model

• Library:

• Simscape / Multibody / Body Elements / Flexible Bodies

• 

Description

The Reduced Order Flexible Solid block models a deformable body of arbitrary geometry based on a reduced-order model.

A reduced-order model is a computationally efficient model that characterizes the mechanical properties of a flexible body under small deformations. The basic data imported from the reduced-order model includes:

• Coordinates and unit quaternions that specify the positions and orientations of all interface frames relative to a common reference frame. See Interface Frames.

• A symmetric stiffness matrix that describes the elastic properties of the flexible body. See Stiffness Matrix.

• A symmetric mass matrix that describes the inertial properties of the flexible body. See Mass Matrix.

If you already have a detailed CAD model of a component in a Simscape™ Multibody™ model, you can use finite-element analysis (FEA) tools to generate the reduced-order data required by this block. For example, with the Partial Differential Equation Toolbox™, you can start with the CAD geometry of your component, generate a finite-element mesh, apply the Craig-Bampton FEA substructuring method, and generate a reduced-order model. For more information, see Model an Excavator Dipper Arm as a Flexible Body.

Common Reference Frame

The block, the reduced-order model, and the CAD geometry must use a consistent common reference frame. This local reference frame defines the x, y, and z directions used to specify the relative position of all points in the body. The reference frame also defines the directions of the small-deformation degrees of freedom (the translations and rotations) associated with each interface frame.

Reduced-Order Model Requirements

Your reduced-order model must contain at least one boundary node. Each boundary node determines the location of an interface frame where the flexible body connects to other Simscape Multibody elements, such as joints, constraints, forces, and sensors. You specify the boundary nodes in the reduced-order model in the same order as the corresponding interface frames on the block.

Each boundary node must contribute six degrees of freedom to the reduced-order model. The degrees of freedom for node i must be retained in the order

U_i = [T_xi, T_yi, T_zi, R_xi, R_yi, R_zi],

where:

• T_xi, T_yi, and T_zi are translational degrees of freedom along the x, y, and z directions.

• R_xi, R_yi, and R_zi are rotational degrees of freedom about the x, y, and z axes.

Your model can also include additional degrees of freedom, D₁, D₂, ⋯, D_m, that correspond to retained normal vibration modes.

The number of degrees of freedom determines the size of the stiffness and mass matrices. In a flexible body with n boundary nodes and m modal degrees of freedom, these matrices have r = 6n + m rows and columns. The order of the rows and columns must correspond to the order of the degrees of freedom:

U_reduced = [U₁, U₂, ⋯, U_n, D₁, D₂, ⋯, D_m].

The more degrees of freedom in the model, the larger the matrices that describe the flexible body and the slower the simulation.

Damping

To specify the damping characteristics of the flexible bodies, this block supports three damping methods: proportional damping, uniform modal damping, and damping matrix methods. For more informations, see Damping.

Simulation Performance

Flexible bodies can increase the numerical stiffness of a multibody model. To avoid simulation issues, use a stiff solver such as ode15s or ode23t.

Damping can significantly influence simulation performance. For example, when modeling a body with little or no damping, undesirable high-frequency modes in the response can slow down the simulation. In that case, adding a small amount of damping can improve the speed of the simulation without significantly affecting the accuracy of the model.

Ports

Frame

F1, F2, ..., Fn — Interface frames

frame

Frames that connect the flexible body to the model. Each interface frame corresponds to a boundary node in the reduced-order model. Interface frames allow you to connect the flexible body to other Simscape Multibody elements, such as joints, constraints, forces, and sensors. It is not required that all frame ports be connected.

The Number of Frames parameter controls the number of interface frame ports on the block. This number must match the number of boundary nodes defined in the original finite element model used to generate the reduced-order model.

In the Origins parameter, specify the origin for each interface frame relative to a common reference frame.

The axes of the interface frames are always aligned with the axes of the reference frame. If you require an interface frame with a different orientation, attach a Rigid Transform block directly to the frame port.

Parameters

Unit System

Unit System — Standard or custom units for length, mass, and time

SI (m, kg, s) (default) | CGS (cm, g, s) | English (ft, slug, s) | Custom

System of units in which to express length, mass, time, and other derived units of measure used in all block parameters. Angle measure is always in radians.

Unit System	Base Units			Selected Derived Units
	Length	Mass	Time	Force	Stress and Pressure	Density
SI	m	kg	s	N = kg·m/s2	Pa = kg/(m·s2)	kg/m3
CGS	cm	g	s	dyn = g·cm/s2	Ba = g/(cm·s2)	g/cm3
English	ft	slug	s	lbf = slug·ft/s2	slug/(ft·s2)	slug/ft3

To specify units of length, mass, and time individually, select Custom. For example, suppose that you specify a custom unit system with mm for length, t for mass, and s for time. The derived units include N = t·mm/s² for force, MPa = t/(mm·s²) for stress and pressure, and t/mm³ for density.

Length Unit — Unit of measure for length

m (default) | cm | mm | km | in | ft | yd | mi

Unit of measure in which to express length.

Dependencies

To enable this parameter, set Unit System to Custom.

Mass Unit — Unit of measure for mass

kg (default) | g | t | lbm | slug

Unit of measure in which to express mass.

Dependencies

To enable this parameter, set Unit System to Custom.

Time Unit — Unit of measure for time

s (default) | ms | min | hr

Unit of measure in which to express time.

Dependencies

To enable this parameter, set Unit System to Custom.

Interface Frames

Number of Frames — Number of frame ports

1 (default) | positive integer literal

Number of interface frame ports. This number must match the number of boundary nodes defined in the original finite element model used to generate the reduced-order model. Specify this parameter by using a positive integer literal. Variables or expressions are not supported.

Origins — Cartesian coordinates of interface frame origins

[0 0 0] (default) | n-by-3 matrix

Cartesian coordinates of all interface frame origins, specified as a matrix with one frame per row. This parameter specifies the position of the boundary nodes defined in the original finite element model used to generate the reduced-order model. All coordinates must be relative to a common reference frame.

Orientations — Orientations of interface frame origins

[1 0 0 0] (default) | n-by-4 matrix of unit quaternions

Orientations of interface frame origins, specified as an n-by-4 matrix of unit quaternions, where n is the number of interface frames.

Reduced Order Matrices

Stiffness Matrix — Stiffness matrix from reduced-order model

[] (default) | r-by-r matrix

Stiffness matrix from the reduced-order model. The stiffness matrix is a symmetric matrix that describes the elastic properties of the flexible body. In a flexible body with n boundary nodes and m dynamic deformation modes, the stiffness matrix has r = 6n + m rows and columns.

Mass Matrix — Mass matrix from reduced-order model

[] (default) | r-by-r matrix

Mass matrix from the reduced-order model. The mass matrix is a symmetric matrix that describes the inertial properties of the flexible body. In a flexible body with n boundary nodes and m dynamic deformation modes, the mass matrix has r = 6n + m rows and columns.

Damping

Type — Type of damping method

Proportional (default) | Damping Matrix | Uniform Modal | None

Damping method to apply to the solid:

• Select Proportional to apply the proportional (or Rayleigh) damping method. This method defines the damping matrix [C] as a linear combination of the mass matrix [M] and stiffness matrix [K]:

  $$[C]=\alpha [M]+\beta [K]$$,

  where α and β are scalar coefficients.

• Select Damping Matrix to use a reduced-order damping matrix that you computed with the stiffness and mass matrices. For example, you can use this option to specify a modal damping model for the flexible solid.

• Select Uniform Modal to apply the uniform modal damping method. This method applies a single damping ratio to all the vibration modes of the solid. The larger the value, the faster vibrations decay.

• Select None to model undamped solids.

Stiffness Coefficient — Coefficient of stiffness matrix

0.001 s (default) | nonnegative scalar

Coefficient, β, of the stiffness matrix. This parameter defines damping proportional to the stiffness matrix [K].

Dependencies

To enable this parameter, set Type to Proportional.

Mass Coefficient — Coefficient of mass matrix

0 1/s (default) | nonnegative scalar

Coefficient, α, of the mass matrix. This parameter defines damping proportional to the mass matrix [M].

Dependencies

To enable this parameter, set Type to Proportional.

Damping Ratio — Damping ratio for uniform modal damping method

0.01 (default) | unitless nonnegative scalar

Damping ratio, ζ, applied to all vibration modes of a solid. The larger the value, the faster the vibrations decay.

• Use ζ = 0 to model undamped solids.

• Use ζ < 1 to model underdamped solids.

• Use ζ = 1 to model critically damped solids.

• Use ζ > 1 to model overdamped solids.

Dependencies

To enable this parameter, set Type to Uniform Modal.

Data Types: double

Damping Matrix — Reduced-order damping matrix

[] (default) | r-by-r matrix

Reduced-order damping matrix. The damping matrix is a symmetric matrix that describes the damping properties of the flexible body. In a flexible body with n boundary nodes and m dynamic deformation modes, the damping matrix has r = 6n + m rows and columns.

Dependencies

To enable this parameter, set Type to Damping Matrix.

Fidelity

Type — Method to model flexible bodies

None (default) | Modally Reduced

Method to use to model flexible bodies, specified as None or Modally Reduced. Set the parameter to None to use full nodal elastic coordinates or set the parameter to Modally Reduced to use the modal transformation method to reduce the elastic coordinates of the body. For both settings, the block uses the floating frame of the reference formulation [1-2] to couple the body with its elastic deformation.

Number of Retained Modes — Retained modes

1 (default) | nonnegative integer

Retained modes, specified as an integer in range [0, n], where n is the number of elastic degrees of freedom of the body. If you set the number to 0 the flexible body is treated as a rigid body.

Dependencies

To enable this parameter, set Type to Modally Reduced.

Graphic

Type — Graphic to use for visualization

None (default) | Partitioned Geometry

Type of the visual representation of the solid, specified as Partitioned Geometry or None. Set the parameter to Partitioned Geometry to show the visual representation of the solid. Set the parameter to None to hide the solid in the model visualization.

File Name — Path of CAD geometry file

custom character vector

Path of the CAD file that defines the undeformed solid geometry, specified as a custom character vector. The file location can be specified as an absolute path starting from the root directory of the file system or a relative path starting from a folder on the MATLAB^® path.

The CAD file must define the geometry of the flexible body by using the same reference frame as the reduced-order model. See Supported Software and File Formats for details of supported file formats.

Example: 'C:/Users/JDoe/Documents/myShape.STEP' or 'Documents/myShape.STEP'

Dependencies

To enable this parameter, set Type to Partitioned Geometry

Unit Type — Source of length unit for geometry

From File (default) | From Unit System

Source of the length unit for the solid geometry of the solid.

• To use the unit specified in the imported CAD geometry, select From File.

• To use the unit specified in the Unit System parameters, select From Unit System. Select this option if your CAD geometry file format does not provide length units.

Dependencies

To enable this parameter, set Type to Partitioned Geometry

Visual Properties — Parameterizations for color and opacity

From File (default) | Advanced | Simple

Parameterization for specifying visual properties.

• Select From File to use color data from the imported CAD geometry file. Note that not all file formats allow color data. In formats that allow color data, that data is often optional. If your file does not specify color, the solid is rendered in gray.

• Select Simple to specify Color and Opacity.

• Select Advanced to specify more visual properties, such as Diffuse Color, Specular Color, Ambient Color, Emissive Color, and Shininess.

Dependencies

To enable this parameter, set Type to Partitioned Geometry

Color — Color of light due to diffuse reflection

[0.5 0.5 0.5] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1 | 4-by-1 or 1-by-4 vector with values in the range of 0 to 1

Color of the graphic under direct white light, specified as an [R G B] or [R G B A] vector on a 0–1 scale. An optional fourth element (A) specifies the color opacity on a scale of 0–1. Omitting the opacity element is equivalent to specifying a value of 1.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Simple

Opacity — Graphic opacity

1.0 (default) | scalar in the range of 0 to 1

Graphic opacity, specified as a scalar in the range of 0 to 1. A scalar of 0 corresponds to completely transparent, and a scalar of 1 corresponds to completely opaque.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Simple

Diffuse Color — Color of light due to diffuse reflection

[0.5 0.5 0.5] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1 | 4-by-1 or 1-by-4 vector with values in the range of 0 to 1

Color of the light due to diffuse reflection, specified as an [R,G,B] or [R,G,B,A] vector with values in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1.

The diffuse color reflects the main color of the rendered solid and provides shading that gives the rendered object a three-dimensional appearance.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Advanced

Specular Color — Color of light due to specular reflection

[0.5 0.5 0.5 1.0] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1 | 4-by-1 or 1-by-4 vector with values in the range of 0 to 1

Color of the light due to specular reflection, specified as an [R,G,B] or [R,G,B,A] vector with values in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1. This parameter changes the color of the specular highlight, which is the bright spot on the rendered solid due to the reflection of the light from the light source.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Advanced

Ambient Color — Color of ambient light

[0.15 0.15 0.15 1.0] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1 | 4-by-1 or 1-by-4 vector with values in the range of 0 to 1

Color of the ambient light, specified as an [R,G,B] or [R,G,B,A] vector with values in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1.

Ambient light refers to a general level of illumination that does not come directly from a light source. The Ambient light consists of light that has been reflected and re-reflected so many times that it is no longer coming from any particular direction. You can adjust this parameter to change the shadow color of the rendered solid.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Advanced

Emissive Color — Self-illumination color

[0.0 0.0 0.0 1.0] (default) | 3-by-1 or 1-by-3 vector with values in the range of 0 to 1

Color due to self illumination, specified as an [R,G,B] or [R,G,B,A] vector in the range of 0 to 1. The vector can be a row or column vector. The optional fourth element specifies the color opacity. Omitting the opacity element is equivalent to specifying a value of 1.

The emission color is color that does not come from any external source, and therefore seems to be emitted by the solid itself. When a solid has a emissive color, the solid can be seen even if there is no external light source.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Advanced

Shininess — Shininess of rendered solid

75 (default) | scalar in the range of 1 to 128

Shininess of the rendered solid, specified as a scalar in the range of 0 to 128. This parameter affects the sharpness of the specular reflections of the rendered solid. A solid with high shininess has a mirror-like appearance, and a solid with low shininess has a more low-gloss or satin appearance.

Dependencies

To enable this parameter, set:

1. Type to Partitioned Geometry

2. Visual Properties to Advanced

Model Examples

Model an Excavator Dipper Arm as a Flexible Body

Use the Reduced Order Flexible Solid block to model a deformable body of arbitrary geometry. Start with the CAD geometry of the body, produce a finite-element mesh, and generate reduced-order data to use with the block.

Open Live Script

Flexible Dipper Arm

Model a flexible dipper arm, such as the arm for an excavator or a backhoe, by using the Reduced Order Flexible Solid block. This block captures the mechanical behavior of a deformable body through reduced-order stiffness and mass matrices that are associated with interface frame locations. In this example, the Partial Differential Equation Toolbox™ is used to create the reduced-order model.

Open Model

References

[1] Shabana, Ahmed A. Dynamics of Multibody Systems. Fourth edition. New York: Cambridge University Press, 2014.

[2] Agrawal, Om P., and Ahmed A. Shabana. “Dynamic Analysis of Multibody Systems Using Component Modes.” Computers & Structures 21, no. 6 (January 1985): 1303–12. https://doi.org/10.1016/0045-7949(85)90184-1.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2019b