sbiosampleerror
Sample error based on error model and add noise to input data
Description
noisydata = sbiosampleerror(inputdata,errormodel,errorparam)
Examples
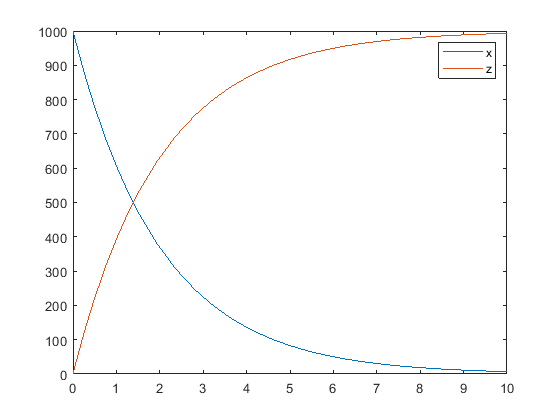
This example adds noise (or error) to the simulation data from a radioactive decay model with the first-order reaction: , where x and z are species and c is the forward rate constant.
Load the sample project containing the radiodecay model m1.
sbioloadproject radiodecay;Simulate the model.
[t,sd,names] = sbiosimulate(m1);
Plot the simulation results.
plot(t,sd); legend(names,'AutoUpdate','off'); hold on
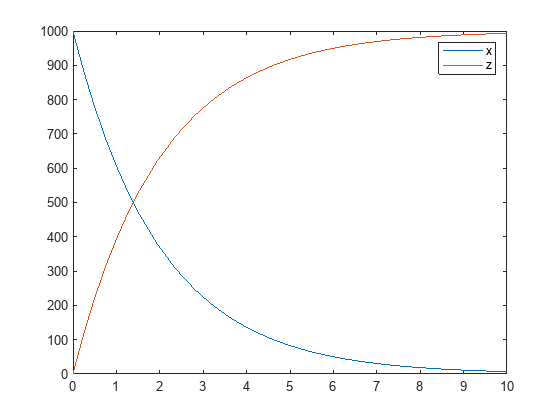
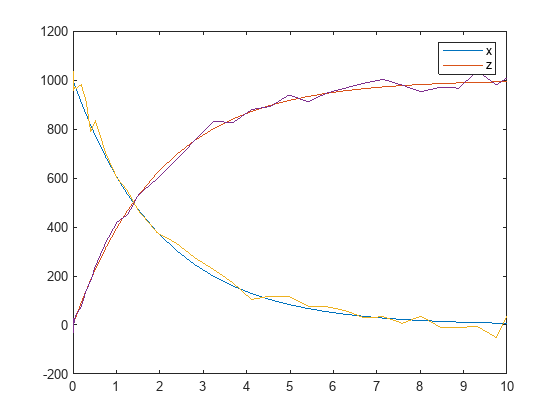
Add noise to the simulation results using the constant error model with the error parameter set to 20.
noisydata = sbiosampleerror(sd,'constant',20);Plot the noisy simulation data.
plot(t,noisydata);
This example defines a custom error model using a function handle and adds noise to simulation data of a radioactive decay model with the first-order reaction 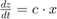 , where
, where x and z are species, and c is the forward rate constant.
Load the sample project containing the radiodecay model m1.
sbioloadproject radiodecay;
Suppose you have a simple custom error model with a standard mean-zero and unit-variance (Gaussian) normal variable e, simulation results f, and two parameters p1 and p2: 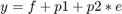
Define a function handle that represents the error model.
em = @(y,p1,p2) y+p1+p2*randn(size(y));
Simulate the model.
[t,sd,names] = sbiosimulate(m1);
Plot the simulation results and hold the plot.
plot(t,sd); legend(names,'AutoUpdate','off'); hold on
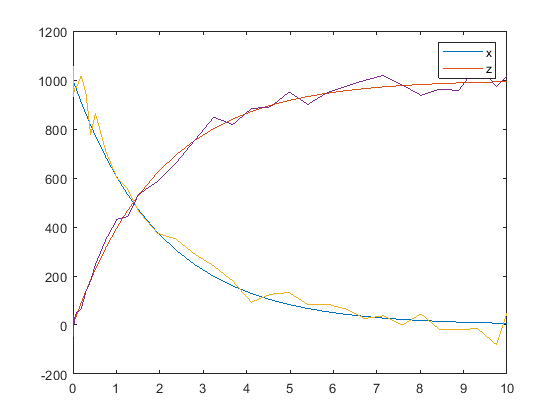
Sample the error using the previously defined custom function with two parameters set to 0.5 and 30, respectively.
noisydata = sbiosampleerror(sd,em,{0.5,30});
Plot the noisy simulation data.
plot(t,noisydata);
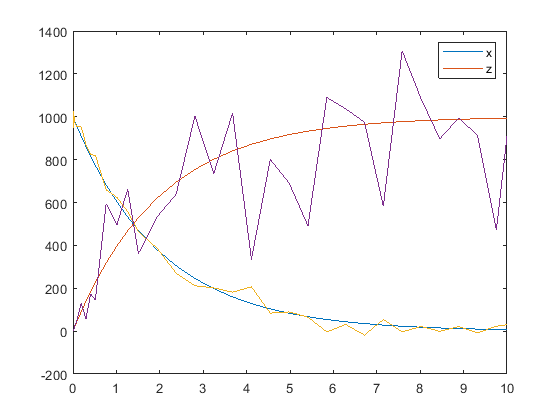
You can also apply a different error model to each state, which is a column in sd. Suppose you want to apply the custom error model (em) to the first column (species x data) and the proportional error model to the second column (species z data).
hold off noisydata = sbiosampleerror(sd,{em,'proportional'},{{0.5,30},0.3}); plot(t,sd); legend(names,'AutoUpdate','off'); hold on plot(t,noisydata);
Input Arguments
Input data, specified as a SimData object, vector of
SimData objects, or numeric matrix. If it is a vector
of SimData objects, the error is added to each of the
columns in the Data property. If it is a numeric matrix, the error is added
to each column in the matrix.
Error model(s), specified as a character vector, string, function handle, string vector, cell array of character vectors, or cell array containing a mixture of character vectors and function handles.
If it is a string vector or cell array, its length must match the number of columns
(responses) in inputdata, and each error model is
applied to the corresponding column in inputdata. If it
is a single character vector, string, or function handle, the same error
model is applied to all columns in inputdata.
The first argument of a function handle must be a matrix of
simulation results. The subsequent arguments are the parameters of
the error model supplied in the errorparam input
argument. The output of the function handle must be a matrix of the
same size as the first input argument (simulation results).
For example, suppose you have a custom error model with a standard mean-zero and unit-variance (Gaussian) normal variable e, simulation results f, and two parameters p1 and p2: . You can define the corresponding function handle as follows.
em = @(y,p1,p2) y+p1+p2*randn(size(y));
y is the matrix of simulation results and
p1 and p2 are the error
parameters. The output of the function handle must be the same size as
y, which is the same as the simulation results
specified in the inputdata input argument. The
parameters p1 and p2 are specified in
the errorparam argument.There are four built-in error models. Each model defines the error using a standard mean-zero and unit-variance (Gaussian) variable e, simulation results f, and one or two parameters a and b. The models are:
'constant':'proportional':'combined':'exponential':
Error model parameter(s), specified as a scalar, vector, or
cell array. If errormodel is 'constant', 'proportional',
or 'exponential', then errorparam is
specified as a numeric scalar. If it is 'combined',
then errorparam is specified as a row vector
with two elements [a b].
If errormodel is a cell array, then errorparam must
be a cell array of the same length. In other words, errorparam must
contain N elements, where N is the number of error models in errormodel.
Each element must have the correct number of parameters for the corresponding
error model.
For example, suppose you have three columns in inputdata, and you are
applying a different error model (constant,
proportional, and exponential
error models with error parameters 0.1,
0.2, and 0.5, respectively) to
each column, then errormodel and
errorparam must be cell arrays with three elements
as follows.
errormodel = {'constant','proportional','exponential'};
errorparam = {0.1,0.2,0.5};Output Arguments
Data with added noise, returned as a vector of SimData
objects or numeric matrix. If inputdata is a vector of
SimData objects, noisydata is
also a vector of SimData objects, and the error is added
to each column in the inputdata.Data property. If
inputdata is specified as a matrix,
noisydata is a matrix, and the error is added to
each column in the matrix.
Version History
Introduced in R2014a
See Also
sbiosampleparameters | createSimFunction | SimFunction object
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)