dct
Discrete cosine transform
Description
y = dct(___,Type=dcttype)
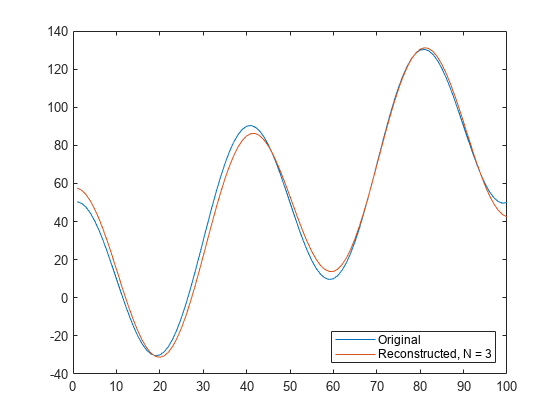
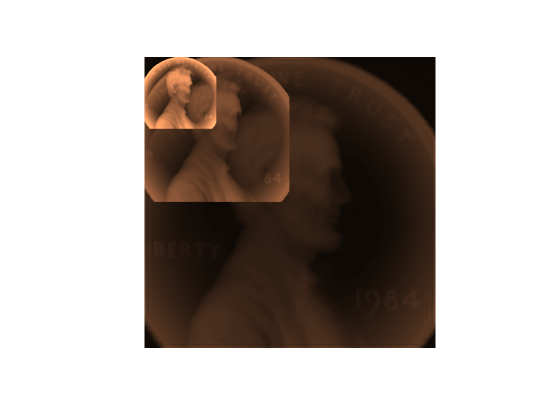
Examples
Input Arguments
Output Arguments
More About
References
[1] Jain, A. K. Fundamentals of Digital Image Processing. Englewood Cliffs, NJ: Prentice-Hall, 1989.
[2] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.
[3] Pennebaker, W. B., and J. L. Mitchell. JPEG Still Image Data Compression Standard. New York: Van Nostrand Reinhold, 1993.
Extended Capabilities
Version History
Introduced before R2006a