structuralBoundaryLoad
(To be removed) Specify boundary loads for structural model
structuralBoundaryLoad will be removed. Use faceLoad,
edgeLoad,
and vertexLoad
instead. (since R2023a) For more information on updating your code, see Version History.
Syntax
Description
structuralBoundaryLoad(
specifies the surface traction, pressure, and translational stiffness on the
boundary of type structuralmodel,RegionType,RegionID,"SurfaceTraction",STval,"Pressure",Pval,"TranslationalStiffness",TSval)RegionType with
RegionID ID numbers.
Surface traction is determined as distributed normal and tangential forces acting on a boundary, resolved along the global Cartesian coordinate system.
Pressure must be specified in the direction that is normal to the boundary. A positive pressure value acts into the boundary (for example, compression). A negative pressure value acts away from the boundary (for example, suction).
Translational stiffness is a distributed spring stiffness for each translational direction. Translational stiffness is used to model an elastic foundation.
structuralBoundaryLoad does not require you to specify
all three boundary loads. Depending on your structural analysis problem, you can
specify one or more boundary loads by picking the corresponding arguments and
omitting others. You can specify translational stiffness for any structural
model. To specify pressure or surface traction,
structuralmodel must be a static, transient, or
frequency response model. Structural models for modal analysis cannot have
pressure or surface traction.
The default boundary load is a stress-free boundary condition.
structuralBoundaryLoad(
specifies concentrated force at a vertex with the structuralmodel,"Vertex",VertexID,"Force",Fval)VertexID
number. You can specify force only if structuralmodel is a
static, transient, or frequency response model. Structural models for modal
analysis cannot have concentrated force.
structuralBoundaryLoad(___,"Vectorized","on")
uses vectorized function evaluation when you pass a function handle as an
argument. If your function handle computes in a vectorized fashion, then using
this argument saves time. See Vectorization. For details on this
evaluation, see Nonconstant Boundary Conditions.
Use this syntax with any of the input arguments from previous syntaxes.
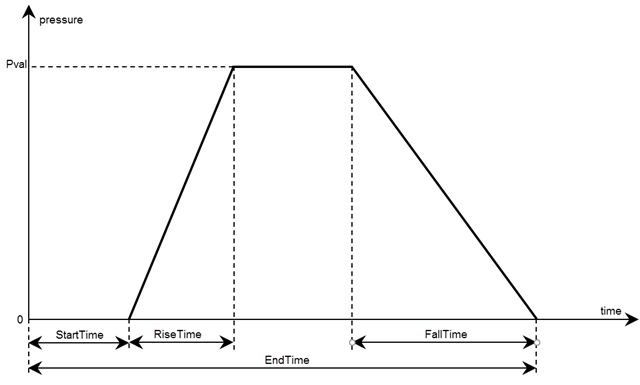
structuralBoundaryLoad(___,"Pressure",
lets you specify the form and duration of a nonconstant pressure pulse and
harmonic excitation for a transient structural model without creating a function
handle. When using this syntax, you must specify the model, region type and
region ID, and pressure. Surface traction and translational stiffness are
optional arguments. This syntax does not work for static, modal analysis, and
frequency response models.Pval,Name,Value)
structuralBoundaryLoad(
lets you specify the form and duration of a nonconstant concentrated force and
harmonic excitation for a transient structural model without creating a function
handle.structuralmodel,"Vertex",VertexID,"Force",Fval,Name,Value)
structuralBoundaryLoad(___,"Label",
adds a label for the structural boundary load to be used by the labeltext)linearizeInput function. This function lets you pass boundary
loads to the linearize function that extracts sparse linear models for use
with Control System Toolbox™.
boundaryLoad = structuralBoundaryLoad(___)