factorTwoPoseSE2

Factor relating two SE(2) poses

Since R2022a

expand all in page

Description

The factorTwoPoseSE2 object contains factors that relate pairs of poses in the SE(2) state space for a factorGraph object.

Creation

Syntax

F = factorTwoPoseSE2(nodeID)
F = factorTwoPoseSE2(nodeID,Name=Value)

Description

F = factorTwoPoseSE2(nodeID) creates a factorTwoPoseSE2 object, F, with the node identification numbers property NodeID set to nodeID.

F = factorTwoPoseSE2(nodeID,Name=Value) specifies properties using one or more name-value arguments. For example, factorTwoPoseSE2([1 2],Measurement=[1 5 7]) sets the Measurement property of the factorTwoPoseSE2 object to [1 5 7].

example

Properties

expand all

This property is read-only.

Node ID numbers, specified as an N-by-2 matrix of nonnegative integers, where N is the total number of desired factors. Each row represents a factor that connects to two nodes of type POSE_SE2 at the specified node IDs in the factor graph. The rows are of the form [PoseID1 PoseID2].

If a factor in the factorTwoPoseSE2 object specifies an ID that does not correspond to a node in the factor graph, the factor graph automatically creates a node of the required type with that ID and adds it to the factor graph when adding the factor to the factor graph.

For more information about the expected node types of all supported factors, see Expected Node Types of Factor Objects.

Measured relative pose, specified as a N-by-3 matrix, where each row is of the form [dx dy dtheta]. N is the total number of factors. dx and dy are the change in position in x and y, respectively, and dtheta is the angle between the two positions.

Information matrix associated with the measurement, specified as a 3-by-3 matrix or a 3-by-3-N matrix. N is the total number of factors specified by this factorTwoPoseSE2 object. Each information matrix corresponds to the measurements of the specified nodes in NodeIDs.

If you specify this property as a 3-by-3 matrix when NodeID contains more than one row, the information matrix corresponds to all measurements in Measurement.

Object Functions

nodeTypeGet node type of node in factor graph

Examples

collapse all

Open Live Script

Define the ground truth for five robot poses as a loop and create a factor graph.

gndtruth = [0 0 0; 
            2 0 pi/2; 
            2 2 pi; 
            0 2 3*pi
            0 0 0];
fg = factorGraph;

Generate the node IDs needed to create three factorTwoPoseSE2 factors. Because node 4 would coincide directly on top of the node 0, instead of specifying a factor that connects node 3 to a new node 4, create a loop closure by adding another factor that relates node 3 to node 0.

poseFIDs = generateNodeID(fg,3,"factorTwoPoseSE2");
poseFIDs = [poseFIDs; 3 0]
poseFIDs = 4×2

     0     1
     1     2
     2     3
     3     0

Define the relative measurement between each consecutive pose and add a little noise so the measurement is more like a sensor reading. 

relMeasure = [2 0 pi/2; 2 0 pi/2; 2 0 pi/2; 2 0 pi/2] + 0.1*rand(4,3);

Create the factorTwoPoseSE2 factors with the defined relative measurements and then add the factors to the factor graph.

poseFactor = factorTwoPoseSE2(poseFIDs,Measurement=relMeasure);
addFactor(fg,poseFactor);

Get the node IDs of all of the SE2 pose nodes in the factor graph.

poseIDs = nodeIDs(fg,NodeType="POSE_SE2");

Because the POSE_SE2 type nodes have a default state of [0 0 0], you should provide an initial guess for the state. Normally this is from an odometry sensor on the robot. But for this example, use the ground truth with some noise.

predictedState = gndtruth(1:4,:);
predictedState(2:4,:) = predictedState(2:4,:) + 0.1*rand(3,3);

Then set the states of the pose nodes to the predicted guess states.

nodeState(fg,poseIDs,predictedState);

Fix the first pose node. Because the nodes are all relative to each other, they need a known state to be an anchor.

fixNode(fg,0);

Optimize Factor Graph and Visual Results

Optimize the factor graph with the default solver options. The optimization updates the states of all nodes in the factor graph so the poses of vehicle update.

rng default
optimize(fg)
ans = struct with fields:
             InitialCost: 6.1614
               FinalCost: 0.0118
      NumSuccessfulSteps: 5
    NumUnsuccessfulSteps: 0
               TotalTime: 1.5998e-04
         TerminationType: 0
        IsSolutionUsable: 1
        OptimizedNodeIDs: [1 2 3]
            FixedNodeIDs: 0

Get and store the updated node states for the robot. Then plot the results, comparing the factor graph estimate of the robot path to the known ground truth of the robot.

poseStatesOpt = nodeState(fg,poseIDs)
poseStatesOpt = 4×3

         0         0         0
    2.0777    0.0689    1.5881
    2.0280    2.1646   -3.1137
    0.0132    2.0864   -1.6014


figure
plot(gndtruth(:,1),gndtruth(:,2),Marker="*",LineWidth=1.5)
hold on
plot([poseStatesOpt(:,1); 0],[poseStatesOpt(:,2); 0],Marker="*",LineStyle="--",LineWidth=1);
legend(["Ground Truth","Opt. Position"]);
s2 = se2(poseStatesOpt,"xytheta");
plotTransforms(s2,FrameSize=0.5,FrameAxisLabels="on");
axis padded
hold off

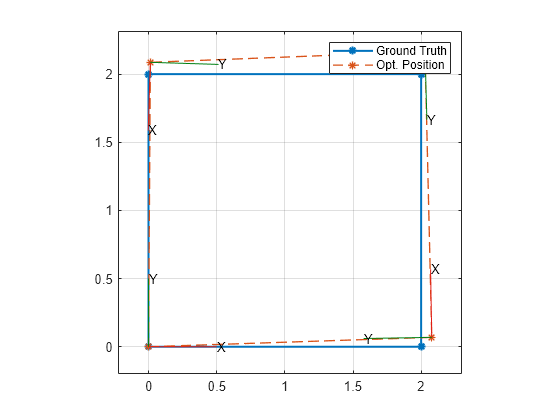
Figure contains an axes object. The axes object contains 22 objects of type patch, line, text. These objects represent Ground Truth, Opt. Position.

Note that the poses do not match perfectly with the ground truth because there are not many factors in this graph that the optimize function can use to provide a more accurate solution. The accuracy can be improved by using more accurate measurements, accurate initial state guesses, and adding additional factors to add more information for the optimizer to use.

More About

expand all

Extended Capabilities

expand all

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2022a

expand all

See Also

Objects