bessely
Bessel function of second kind
Description
Y = bessely(
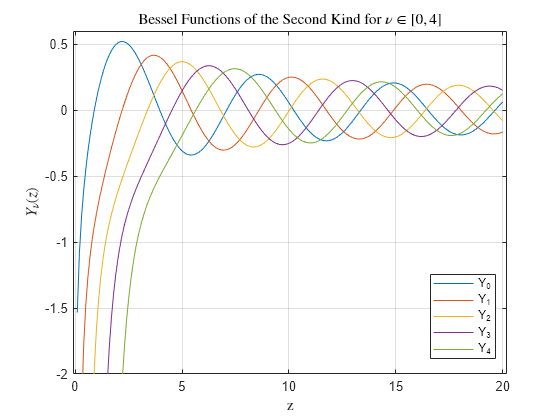
computes the Bessel function of the
second kind
Yν(z) for each element in array nu,Z)Z.
Examples
Input Arguments
More About
Tips
The Bessel functions are related to the Hankel functions, also called Bessel functions of the third kind:
is besselh, Jν(z) is besselj, and Yν(z) is bessely. The Hankel functions also form a fundamental
set of solutions to Bessel's equation (see besselh).
References
[1] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.
Extended Capabilities
Version History
Introduced before R2006a